题目描述:
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
思路分析:
这个题目有一个限制条件,就是只能买卖一次,从他的物理意义看就是求左右数字的最大间隔。但是这个题目也可以使用动态规划的方法来做。
1.确定DP数组的下标及含义
买卖股票的问题都是将dp设置为一个2维数组,形状是[len(days)][2],分别用于表示当天不持有股票和当天持有股票的最大收益。
点击查看代码
// 持有股票:取前一天持有股票的状态,或今天买入股票后的状态
dp[i][0] = max(dp[i-1][0], -prices[i])
// 不持有股票:取前一天不持有股票的状态,或今天卖出股票后的状态
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
这种设计能覆盖单次买卖、无限次买卖的决策路径,通过状态转移方程体现连续性.
二、复杂场景下的不足(需扩展维度)
多交易限制(如最多k次交易)
问题:当交易次数受限(如LeetCode 123、188),二维数组无法区分不同交易次数的状态。
解决方案:
使用三维数组 dp[len][k+1][2],或压缩为二维数组 dp[len][2k+1]。
状态示例:
dp[i][2j+1]:第j次买入后的状态
dp[i][2j+2]:第j次卖出后的状态
特殊条件(冷冻期、手续费)
冷冻期问题(LeetCode 309):需引入三种状态:
dp[i][0]:持有股票
dp[i][1]:不持有且处于冷冻期
dp[i][2]:不持有且非冷冻期
手续费问题(LeetCode 714):在卖出时扣除手续费,需调整状态转移方程
点击查看代码
//动态规划是记录子问题(状态)的答案。想得到最后状态的答案,有目的性,那就应该保存每个元素的每个状态的可能的值,得到每个元素的每种情况的状态值,从而得到最后的答案。
func maxProfit(prices []int) int {
if len(prices) == 0 {
return 0
}
// 初始化 dp 数组,dp[i][0] 表示第 i 天持有股票的最大利润,dp[i][1] 表示第 i 天不持有股票的最大利润
dp := make([][]int, len(prices))
for i := 0; i < len(dp); i++ {
dp[i] = make([]int, 2)
}
// 初始状态
dp[0][0] = -prices[0] // 第 0 天持有股票的最大利润,即买入后的净利润
dp[0][1] = 0 // 第 0 天不持有股票的最大利润,即没有交易时的收益为 0
// 动态规划转移方程
for i := 1; i < len(prices); i++ {
// 持有股票:取前一天持有股票的状态,或今天买入股票后的状态
dp[i][0] = max(dp[i-1][0], -prices[i])
// 不持有股票:取前一天不持有股票的状态,或今天卖出股票后的状态
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
}
// 返回最后一天不持有股票的最大利润
return dp[len(prices)-1][1]
}
此类题型的不同题目的解决方案
1.可以买卖股票多次,注意只有一只股票,所以再次购买前要出售掉之前的股票。
- dp[i][0] 表示第i天持有股票所得现金。
- dp[i][1] 表示第i天不持有股票所得最多现金
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
2. 至多买卖两次股票
- 这个情况的DP数组就有5中情况:
没有操作
第一次买入
第一次卖出
第二次买入
第二次卖出
dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
数组的初始化:
dp[0][0] = 0; dp[0][1] = -prices[0]; dp[0][2] = 0; dp[0][3] = -prices[0]; dp[0][4] = 0;
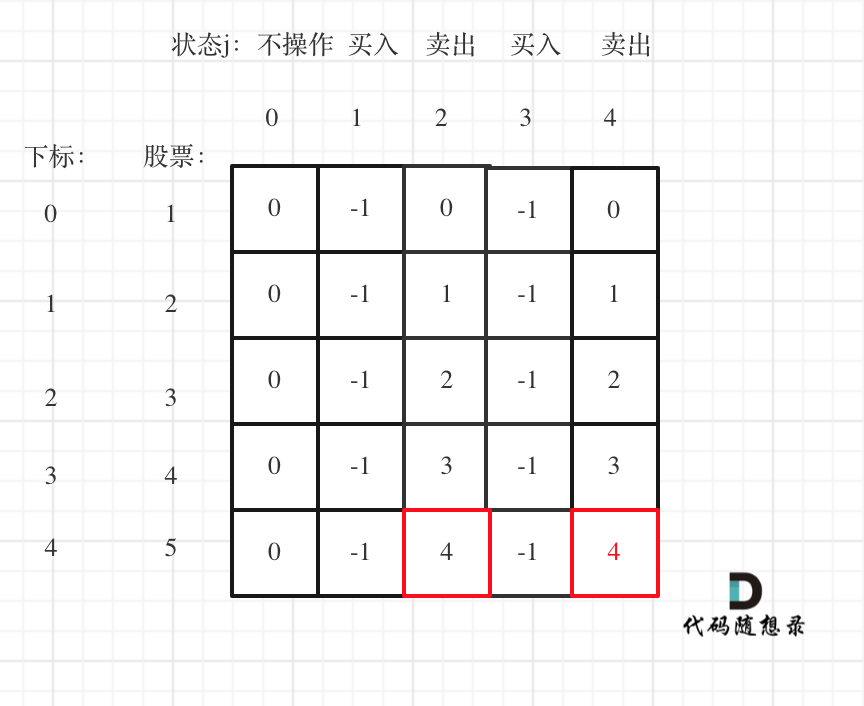
可以看到红色框为最后两次卖出的状态。
现在最大的时候一定是卖出的状态,而两次卖出的状态现金最大一定是最后一次卖出。
所以最终最大利润是dp[4][4]
3.最多可以进行K笔交易
这个题目可以和最多进行2笔交易的题目进行类比。他们相同的点都是买了必须卖,如何进行DP维度的拓展?除了0以外,偶数就是保持卖出,奇数就是保持买入。
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
数组初始化
主要是买入==》 dp[0][j]当j为奇数的时候都初始化为 -prices[0]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号