01背包问题 Golang实现

背包问题的分类：

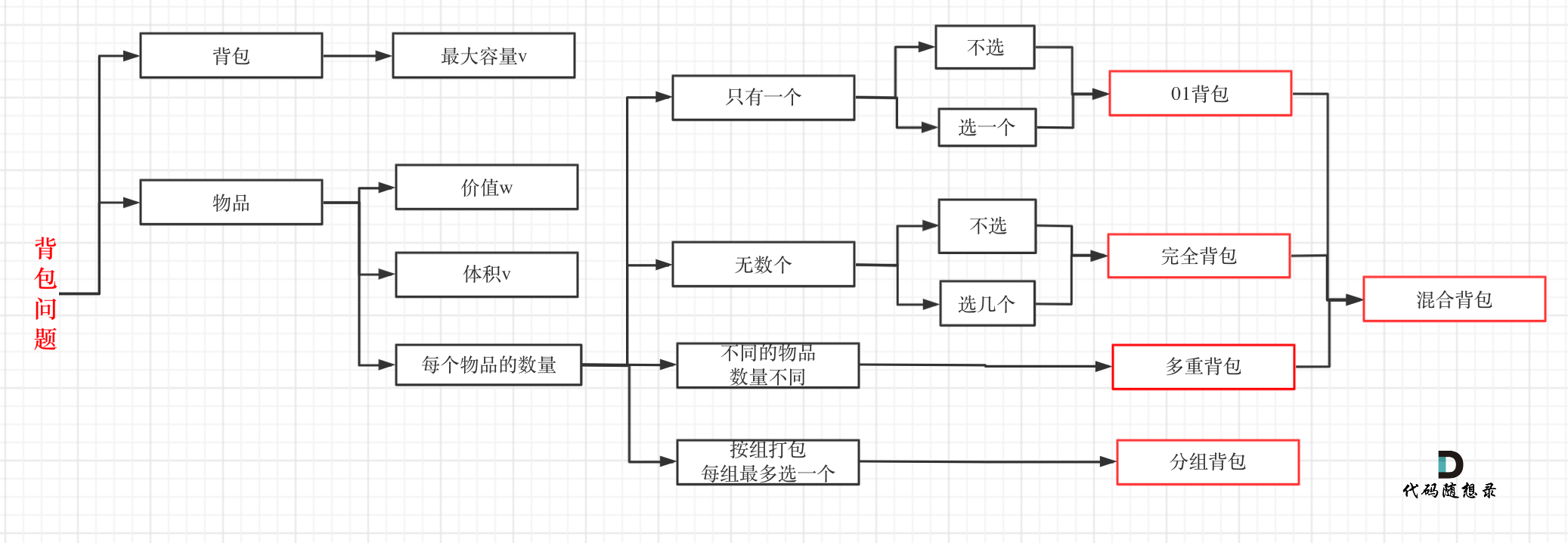
01 背包描述：

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

思路分析：

1. 问题核心：
   从给定的 𝑛 个物品中，以背包容量 𝑉为约束，寻找一种选择方式，使得总价值最大化。

二维数组

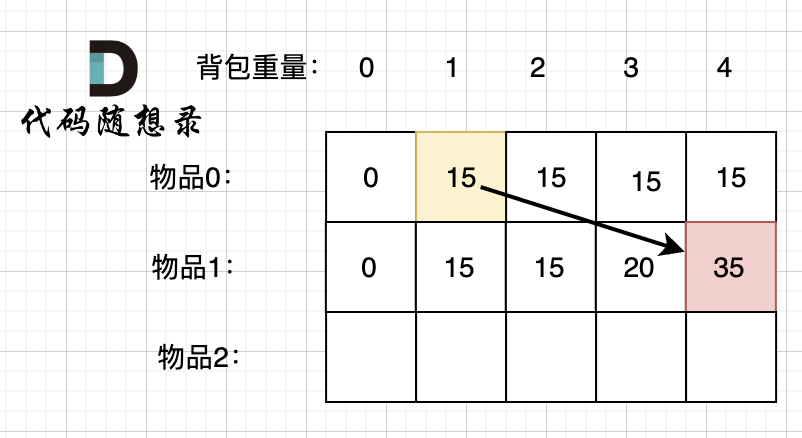
动态规划的核心就是记录子问题的解决答案，然后后续问题可以由之前的子问题的答案推导出来，所以最直观的想法就是使用二维数组来记录各个容量下能选择的最大总价值，然后不断更新得到最后的答案。

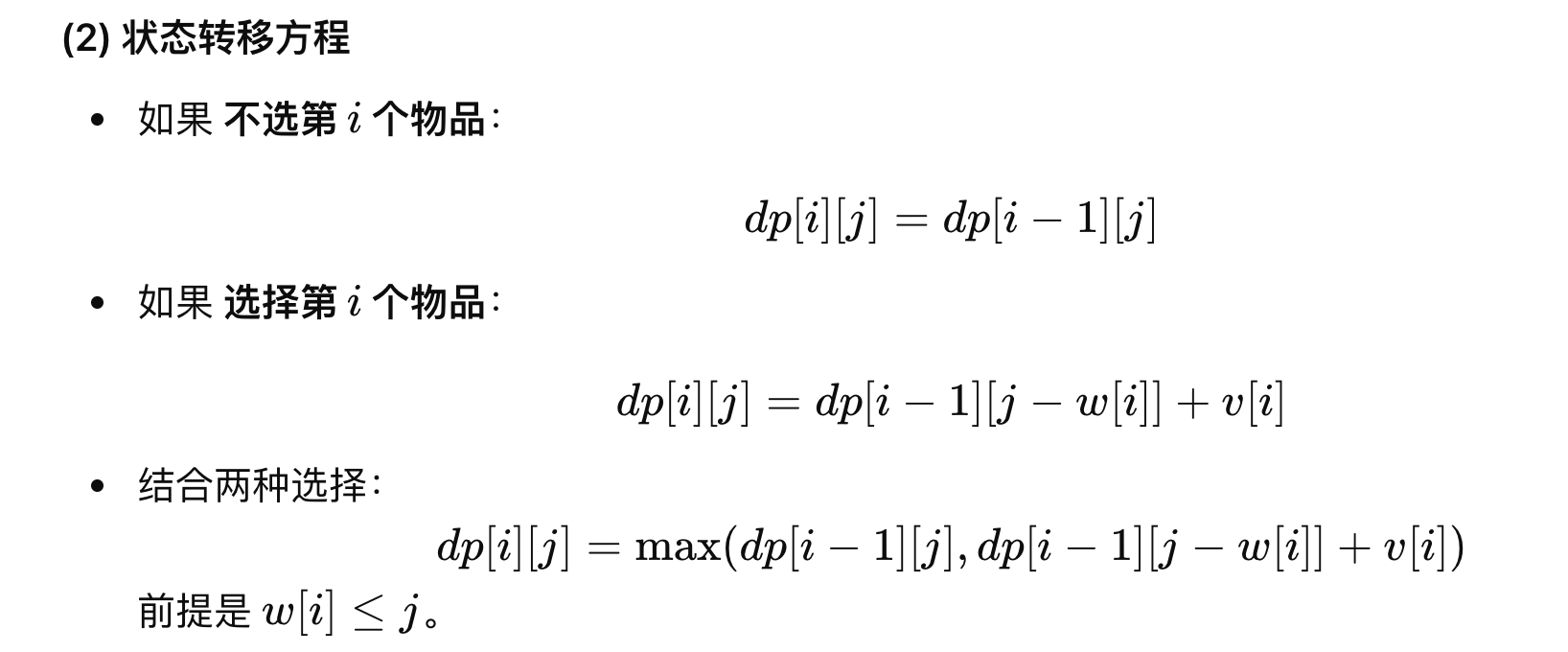
点击查看代码

func knapsack(V int, n int, vw [][]int) int {
	dp := make([][]int, n+1)
	for i := range dp {
		dp[i] = make([]int, V+1)
	}

	for i := 1; i <= n; i++ {
		for j := 1; j <= V; j++ {
			dp[i][j] = dp[i-1][j] // 不选当前物品
			if vw[i-1][1] <= j { // 选择当前物品
				dp[i][j] = max(dp[i][j], dp[i-1][j-vw[i-1][1]]+vw[i-1][0])
			}
		}
	}

	return dp[n][V]
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

---

滚动数组解法

滚动体现在每次都是从V开始遍历，他的上一趟表示的是N-1范围的物品的选取情况。每次必须从后往前，因为当前状态需要子问题的答案，如果从0-V，子问题的答案会被覆盖，导致后续问题无法查询到子问题的记录。

点击查看代码

func knapsack(V int, n int, vw [][]int) int {
    dp := make([]int, V+1)

    for i := 0; i < n; i++ {
        for j := V; j >= vw[i][1]; j-- {
            dp[j] = max(dp[j], dp[j-vw[i][1]] + vw[i][0])
        }
    }

    return dp[V]
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}