题目描述:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 2, n = 3
输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
思路分析:
动态规划入门
动态规划(Dynamic Programming,DP)的核心思想是将问题拆解为子问题,通过记录这些子问题的答案来避免重复计算,从而提高计算效率。具体来说,当我们解决一个大问题时,先解决它的子问题,并将这些子问题的最优解存储在一个表格(通常是数组或矩阵)中。在之后的计算过程中,可以直接查找表格中存储的解,而不必重新计算。
动态规划问题通常需要满足两个条件:
- 最优子结构(Optimal Substructure):问题的最优解可以通过子问题的最优解推导出来。也就是说,解决一个大问题时,可以通过合并多个子问题的解来得到最终的解。
- 重叠子问题(Overlapping Subproblems):问题可以被分解成多个相同的子问题,这些子问题在计算过程中会重复出现,因此适合用记忆化搜索或表格存储来避免重复计算。
- 无后效性:一旦某一个子问题的求解结果确定以后,就不会再被修改。
解决动态规划问题有两种常见的思考方式:
-
自顶向下(Top-down):这种方法通常采用递归的方式解决问题,并结合记忆化技术(Memoization)来记录子问题的解。通过递归函数的调用,我们可以从最终问题逐步向子问题推导,并在每次调用时检查是否已经计算过该子问题,若已计算,则直接返回结果,避免重复计算。
-
自底向上(Bottom-up):自底向上的方法先从最小的子问题开始逐步解决,直到最终问题。这通常通过填充表格的方式实现。自底向上的动态规划在实现上通常更高效,因为它不涉及递归的开销,并且可以更清晰地展现问题的结构。
解决动态规划的5个步骤
在解决动态规划(DP)问题时,通常需要以下几个步骤来构建和推导出解决方案:
1. 确定 dp 数组(DP table)以及下标的含义
dp 数组是用来存储子问题的解的数组。它的定义通常依赖于问题的状态。例如,如果问题涉及到某个选择的状态或某个过程的步骤,dp[i] 就表示某个特定状态下的问题解。
- 状态:
dp[i]表示问题在某一特定条件下的最优解(可能是最大值、最小值、次数等)。 - 下标的含义:根据问题的特性,
i表示当前的状态或问题的规模。比如在背包问题中,i可能表示背包容量;在最短路径问题中,i可能表示某个节点。
2. 确定递推公式
递推公式描述了如何根据已解决的子问题来计算更大的问题的解。递推公式是动态规划问题的核心,它直接决定了算法的时间复杂度。
- 递推公式通常是通过分析问题的结构得出的。
- 它表示如何将子问题的解合并来得到更大问题的解。
- 对于某些问题,可能有多种递推公式(不同的状态转移方式),需要选择最合适的一种。
3. dp 数组如何初始化
初始化 dp 数组是动态规划的一个重要步骤。初始化通常是根据问题的边界条件来确定的。
- 边界条件:通常是
dp[0]或dp[1]等特殊情况。例如,在背包问题中,当背包容量为 0 时,最大价值为 0;在最短路径问题中,起始节点的距离通常初始化为 0,其他节点初始化为无穷大。 - 基础状态:在一些问题中,可能需要根据初始条件来填充
dp数组的某些部分,例如初始状态的解。
4. 确定遍历顺序
遍历顺序决定了 dp 数组的填充顺序,也就是决定了子问题的解的计算顺序。通常有两种常见的遍历方式:
- 从小到大(自底向上):从最小的子问题开始计算,逐步扩展到更大的问题。常用于问题的规模逐渐增大的情况。
- 从大到小(自顶向下):从较大的子问题开始计算,逐步将其拆解为更小的子问题。这个方法在递归的情况下尤为常见。
5. 举例推导 dp 数组
让我们通过一个经典的动态规划问题来说明这些步骤:0/1 背包问题。
问题描述:
给定一个背包容量 W 和 n 个物品,每个物品有一个重量和价值。问:如何选择物品放入背包,使得背包内的物品总价值最大,且总重量不超过背包容量。
步骤解析:
-
确定
dp数组的含义:- 定义
dp[i][w]为前i个物品中,背包容量为w时的最大价值。 i表示当前考虑的物品的编号(1 到n)。w表示当前背包的容量(0 到W)。
- 定义
-
确定递推公式:
对于每个物品i和背包容量w,有两种选择:- 不放入物品
i,则dp[i][w] = dp[i-1][w]。 - 放入物品
i,则dp[i][w] = dp[i-1][w-weight[i]] + value[i](前提是当前背包容量w足够容纳物品i)。
递推公式为:
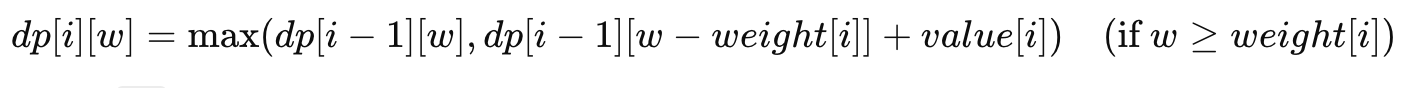
- 不放入物品
-
初始化
dp数组:dp[0][w] = 0:表示没有物品时,背包的最大价值为 0。dp[i][0] = 0:表示背包容量为 0 时,不管有多少物品,最大价值都为 0。
-
确定遍历顺序:
- 从小到大遍历:首先遍历物品
i从1到n,然后对每个物品遍历背包容量w从1到W。
- 从小到大遍历:首先遍历物品
-
举例推导
dp数组:
假设有 3 个物品,背包容量为 4。物品的重量和价值分别为:- 物品 1: 重量 2, 价值 3
- 物品 2: 重量 1, 价值 2
- 物品 3: 重量 3, 价值 4
初始化
dp数组:
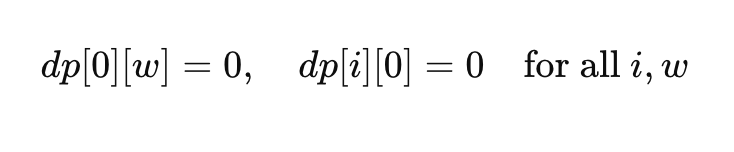
填充
dp数组:-
考虑物品 1,容量从 1 到 4:
dp[1][1] = 0(不能放入物品 1)dp[1][2] = 3(可以放入物品 1)dp[1][3] = 3(可以放入物品 1)dp[1][4] = 3(可以放入物品 1)
-
考虑物品 2,容量从 1 到 4:
dp[2][1] = 2(可以放入物品 2)dp[2][2] = 3(可以放入物品 1 或物品 2)dp[2][3] = 3(可以放入物品 1 或物品 2)dp[2][4] = 5(可以放入物品 1 和物品 2)
-
考虑物品 3,容量从 1 到 4:
dp[3][1] = 2dp[3][2] = 3dp[3][3] = 4(可以放入物品 3)dp[3][4] = 5(可以放入物品 2 和物品 3)
最终
dp[3][4] = 5,表示最大价值是 5。
总结:
- dp 数组:用于存储子问题的解。
- 递推公式:描述如何通过子问题的解来推导出更大问题的解。
- 初始化:根据边界条件初始化
dp数组。 - 遍历顺序:确定从哪个子问题开始计算,以确保可以使用已经计算出的结果。
通过这种方式,我们可以逐步推导出问题的最终解。
本题解法
本题都是从左上角出发,要求达到右下角。每次只能向右或者向下,就是这两种选择。那么以此为例: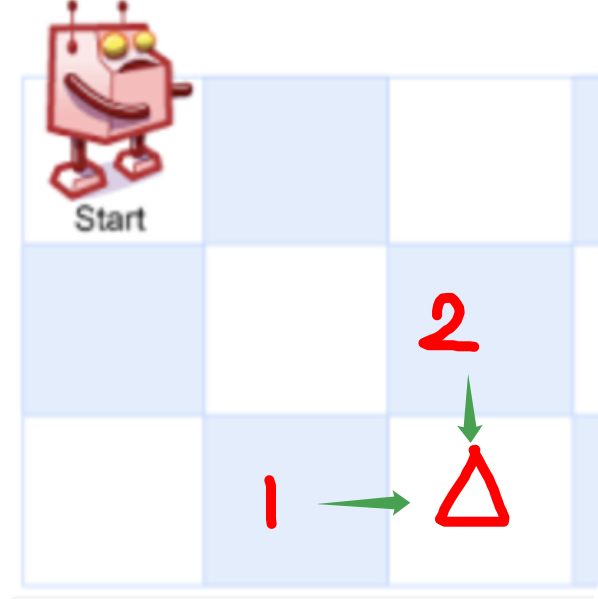
想要到达三角形处,有两种选择:
1.从1处向右一格
2.从2处向下一格
所以:\(dp[i][j] = dp[i - 1][j] + dp[i][j - 1]\).那我们要求的是到指定点的路径条数,\(dg[i][j]\)很自然就是到达指定点的路径条数。
- 初始化分析
在动态规划问题中,初始值非常重要。初始值通常是边界条件,它决定了在计算其他值时的起始状态。
假设我们从坐标 (0, 0) 开始:
\(dp[0][0] = 1\):这是起点,表示从起点到起点有 1 条路径(即起点本身)。
如果没有其他选择(例如,格子外部或障碍物),则第一行和第一列的值都是 1,因为它们只有一种路径:一直从左或从上到达。
\(dp[0][j] = 1\)(对于所有 j),表示从 (0, 0) 到达第一行的任何位置都有 1 条路径(只能从左走)。
\(dp[i][0] = 1\)(对于所有 i),表示从 (0, 0) 到达第一列的任何位置也有 1 条路径(只能从上走)。
Note: 注意go语言初始化二维数组的方法。
点击查看代码
func uniquePaths(m int, n int) int {
dp:= make([][]int,m)
for i := 0; i < m; i++ {
dp[i] = make([]int, n)
}
dp[0][0] = 1
for i := 0; i < m; i++ {
dp[i][0] = 1
}
for i := 0; i < n; i++ {
dp[0][i] = 1
}
for i := 1; i < m; i++ {
for j := 1; j < n; j++ {
dp[i][j] = dp[i-1][j]+dp[i][j-1]
}
}
return dp[m-1][n-1]
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号