NOIP 2025 游记（同步赛）

吐槽

我怀疑这次的 NOIP 出题人是不是 P 话说多了，把 NOIP 的 P 说没了，然后就变成了 NOI 难度（黄紫黑黑）。

经过

T1 —— 糖果店 / candy

题面

题目描述

小 X 开了一家糖果店，售卖 \(n\) 种糖果，每种糖果均有无限颗。对于不同种类的糖果，小 X 采用了不同的促销策略。具体地，对于第 \(i\) (\(1 \le i \le n\)) 种糖果，购买第一颗的价格为 \(x_i\) 元，第二颗为 \(y_i\) 元，第三颗又变回 \(x_i\) 元，第四颗则为 \(y_i\) 元，以此类推。

小 R 带了 \(m\) 元钱买糖果。小 R 不关心糖果的种类，只想得到数量尽可能多的糖果。你需要帮助小 R 求出，\(m\) 元钱能购买的糖果数量的最大值。

输入格式

输入的第一行包含两个正整数 \(n, m\)，代表糖果的种类数和小 R 的钱数。

输入的第 \(i+1\) (\(1 \le i \le n\)) 行包含两个正整数 \(x_i, y_i\)，分别表示购买第 \(i\) 种糖果时第奇数颗的价格和第偶数颗的价格。

输出格式

输出一行一个非负整数，表示 \(m\) 元钱能购买的糖果数量的最大值。

输入输出样例 #1

输入 #1

2 10
4 1
3 3

输出 #1

4

输入输出样例 #2

输入 #2

3 15
1 7
2 3
3 1

输出 #2

8

说明/提示

【样例 1 解释】

小 R 可以购买 4 颗第一种糖果，共花费 \(4 + 1 + 4 + 1 = 10\) 元。

【样例 2 解释】

小 R 可以购买 1 颗第一种糖果、1 颗第二种糖果与 6 颗第三种糖果，共花费 \(1 + 2 + 12 = 15\) 元。

【样例 3】

见选手目录下的 candy/candy3.in 与 candy/candy3.ans。

该样例满足测试点 \(6\) 的约束条件。

【样例 4】

见选手目录下的 candy/candy4.in 与 candy/candy4.ans。

该样例满足测试点 \(8,9\) 的约束条件。

【样例 5】

见选手目录下的 candy/candy5.in 与 candy/candy5.ans。

该样例满足测试点 \(11,12\) 的约束条件。

【样例 6】

见选手目录下的 candy/candy6.in 与 candy/candy6.ans。

该样例满足测试点 \(13\) 的约束条件。

【样例 7】

见选手目录下的 candy/candy7.in 与 candy/candy7.ans。

该样例满足测试点 \(17,18\) 的约束条件。

【数据范围】

对于所有测试数据，均有：

• \(1 \le n \le 10^5\)；
• \(1 \le m \le 10^{18}\)；
• 对于所有 \(1 \le i \le n\)，均有 \(1 \le x_i, y_i \le 10^9\)。

::cute-table{tuack}

测试点编号	\(n \le\)	\(m \le\)	特殊性质
\(1\)	\(1\)	\(10\)	无
\(2,3\)	\(2\)	\(20\)	^
\(4,5\)	\(10\)	^	^
\(6\)	\(10^2\)	\(10^2\)	A
\(7\)	^	^	B
\(8,9\)	^	^	无
\(10\)	\(10^3\)	\(10^4\)	A
\(11,12\)	^	^	B
\(13\)	^	^	无
\(14\)	\(10^5\)	\(10^9\)	A
\(15,16\)	^	^	B
\(17,18\)	^	^	无
\(19,20\)	^	\(10^{18}\)	^

特殊性质 A：对于所有 \(1 \le i \le n\)，均有 \(x_i = y_i\)。

特殊性质 B：对于所有 \(1 \le i \le n\)，均有 \(x_i \ge y_i\)。

00:05

瞪眼一面：什么？糖果？我记得 bbpp 给我在去研学的路上也讲过一个有关糖果的题（似乎有点关系？），这让我充满了决心。

00:10

这个题有两个部分分挺好拿，先拿了再说。唔…… 终于写出来了，这次比赛不至于爆 \(0\) 了。

00:15

噫！好！我中了！我想到正解了！我们考虑一种物品只有两种取法：连续几个 \(a + b\) 加上或不加上 \(a\)。容易发现选 \(a + b\) 捆绑的部分一定是 \(\min\{a + b\}\)，且其他的不选，其中反证法易证。于是我们先选 \(a + b\) 的部分，后面的 \(a\) 直接枚举即可。

00:35

终于调好了（写怎么慢可能是我码力太差了。），感觉良好，至少有一道 AC。

T2 —— 清仓甩卖 / sale

题面

题目描述

小 X 的糖果促销策略很成功，现在糖果店只剩下了 \(n\) 颗糖果，其中第 \(i\) (\(1 \le i \le n\)) 颗糖果的原价为 \(a_i\) 元。小 X 计划将它们全部重新定价，清仓甩卖。具体地，小 X 会将每颗糖果的清仓价格分别定为 1 元或 2 元。设第 \(i\) (\(1 \le i \le n\)) 颗糖果的清仓价格为 \(w_i \in \{1,2\}\) 元，则它的性价比被定义为原价与清仓价格的比值，即 \(\frac{a_i}{w_i}\)。

小 R 又带了 \(m\) 元钱买糖果。这一次，小 R 希望他购买到的糖果的原价总和最大，于是他采用了以下购买策略：将所有糖果按照性价比从大到小排序，然后依次考虑每一颗糖果。具体地，若小 R 在考虑第 \(i\) (\(1 \le i \le n\)) 颗糖果时剩余的钱至少为 \(w_i\) 元，则他会购买这颗糖果；否则他会跳过这颗糖果，继续考虑下一颗。特别地，若存在两颗糖果的性价比相同，则小 R 会先考虑原价较高的糖果；若存在两颗糖果的性价比与原价均相同，则小 R 会先考虑编号较小的糖果。

例如，若小 X 的糖果商店剩余 3 颗糖果，原价分别为 \(a_1=1\)，\(a_2=3\)，\(a_3=5\)，而清仓价格分别为 \(w_1=w_2=1\)，\(w_3=2\)，则性价比分别为 \(1, 3, \frac{5}{2}\)。因此小 R 会先考虑第 2 颗糖果，然后考虑第 3 颗糖果，最后考虑第 1 颗糖果。

小 R 想知道，在小 X 的所有 \(2^n\) 种定价方案中，有多少种定价方案使得他按照上述购买策略能购买到的糖果的原价总和最大。你需要帮助小 R 求出满足要求的定价方案的数量。由于答案可能较大，你只需要求出答案对 \(998,244,353\) 取模后的结果。

输入格式

本题包含多组测试数据。

输入的第一行包含两个非负整数 \(c, t\)，分别表示测试点编号与测试数据组数。\(c=0\) 表示该测试点为样例。

接下来依次输入每组测试数据，对于每组测试数据：

• 第一行包含两个正整数 \(n, m\)，分别表示糖果的数量与小 R 的钱数；
• 第二行包含 \(n\) 个正整数 \(a_1, a_2, \ldots, a_n\)，分别表示每颗糖果的原价。

输出格式

对于每组测试数据，输出一行一个非负整数，表示使得小 R 购买到的糖果的原价总和达到最大值的定价方案数对 \(998,244,353\) 取模后的结果。

输入输出样例 #1

输入 #1

0 1
3 2
1 3 5

输出 #1

6

说明/提示

【样例 1 解释】

该样例即为【题目描述】中的例子。共有以下 6 种定价方案使得小 R 购买到的糖果原价总和最大，分别为：

• \(w_1 = w_2 = w_3 = 1\)，小 R 购买到的糖果原价总和为 8；
• \(w_1 = w_3 = 1\)，\(w_2 = 2\)，小 R 购买到的糖果原价总和为 6；
• \(w_1 = 1\)，\(w_2 = w_3 = 2\)，小 R 购买到的糖果原价总和为 5；
• \(w_2 = w_3 = 1\)，\(w_1 = 2\)，小 R 购买到的糖果原价总和为 8；
• \(w_3 = 1\)，\(w_1 = w_2 = 2\)，小 R 购买到的糖果原价总和为 5；
• \(w_1 = w_2 = w_3 = 2\)，小 R 购买到的糖果原价总和为 5。

注意：若 \(w_1 = w_2 = 1\)，\(w_3 = 2\)，则小 R 会依次购买第 2 颗和第 1 颗糖果，原价总和为 4，但小 R 可以只购买第 3 颗糖果，原价总和为 5。因此该定价方案无法使小 R 购买到的糖果的原价总和达到最大值。

【样例 2】

见选手目录下的 sale/sale2.in 与 sale/sale2.ans。

该样例满足测试点 \(1 \sim 3\) 的约束条件。

【样例 3】

见选手目录下的 sale/sale3.in 与 sale/sale3.ans。

该样例满足测试点 \(4,5\) 的约束条件。

【样例 4】

见选手目录下的 sale/sale4.in 与 sale/sale4.ans。

该样例满足测试点 \(7 \sim 9\) 的约束条件。

【样例 5】

见选手目录下的 sale/sale5.in 与 sale/sale5.ans。

该样例满足测试点 \(10 \sim 12\) 的约束条件。

【样例 6】

见选手目录下的 sale/sale6.in 与 sale/sale6.ans。

该样例满足测试点 \(13\) 的约束条件。

【样例 7】

见选手目录下的 sale/sale7.in 与 sale/sale7.ans。

该样例满足测试点 \(14,15\) 的约束条件。

【样例 8】

见选手目录下的 sale/sale8.in 与 sale/sale8.ans。

该样例满足测试点 \(17\) 的约束条件。

【样例 9】

见选手目录下的 sale/sale9.in 与 sale/sale9.ans。

该样例满足测试点 \(19,20\) 的约束条件。

【样例 10】

见选手目录下的 sale/sale10.in 与 sale/sale10.ans。

该样例满足测试点 \(21 \sim 23\) 的约束条件。

【样例 11】

见选手目录下的 sale/sale11.in 与 sale/sale11.ans。

该样例满足测试点 \(24,25\) 的约束条件。

【数据范围】

设 \(N\) 为单个测试点内所有测试数据的 \(n\) 的和。对于所有测试数据，均有：

• \(1 \le t \le 5 \times 10^4\)；
• \(1 \le n \le 5,000\)，\(N \le 5 \times 10^4\)，\(1 \le m \le 2n - 1\)；
• 对于所有 \(1 \le i \le n\)，均有 \(1 \le a_i \le 10^9\)。

测试点编号	\(n \le\)	\(N \le\)	\(m\)	特殊性质
\(1\sim 3\)	\(5\)	\(5{,}000\)	\(\le 2n - 1\)	无
\(4,5\)	\(10\)	^	^	^
\(6\)	\(40\)	^	^	^
\(7\sim 9\)	\(300\)	^	\(=2\)	^
\(10\sim 12\)	^	^	\(\le 2n - 1\)	B
\(13\)	^	^	^	无
\(14,15\)	\(10^3\)	\(10^4\)	\(=2\)	^
\(16\)	^	^	\(=2n - 1\)	^
\(17\)	^	^	\(=2n - 2\)	^
\(18\)	^	^	\(\le 2n - 1\)	A
\(19,20\)	^	^	^	B
\(21\sim 23\)	^	^	^	无
\(24,25\)	\(5{,}000\)	\(5 \times 10^4\)	^	^

特殊性质 A：\(a_1 = a_2 = \cdots = a_n\)。

特殊性质 B：对于所有 \(1 \le i \le n\)，均有 \(a_i > 5 \times 10^8\)。

00:45

终于读完题面了，不是这题我连不计算方案直接写贪心都不会，背包 \(\Theta(nV)\) 直接爆炸，这题不会更今年 S 组最后一题一样是个紫的神秘 DP 吧？！不管了，先打个 \(20\) 分暴力。

01:15

暴力写完了，来看看特殊性质。\(m = 2n − 1\)、\(A\) 随推一下，答案为 \(2 ^ n\)。

01:35

正解还是想不出来，哎，放弃了。

树的价值 / tree

题面

题目描述

给定一棵 \(n\) 个结点的有根树，其中结点 1 为根，结点 \(i\) (\(2 \le i \le n\)) 的父亲结点为结点 \(p_i\)。

对于 \(1 \le i \le n\)，定义结点 \(i\) 的深度 \(d_i\) 为结点 1 到结点 \(i\) 的简单路径的边数，也就是说，\(d_1 = 0\)，\(d_i = d_{p_i} + 1\) (\(2 \le i \le n\))。定义有根树的高度 \(h\) 为所有结点的深度的最大值，即 \(h = \max_{i=1}^{n} d_i\)。

给定高度的上界 \(m\)。在本题中，给定的有根树的高度不超过 \(m\)。

你需要给每个结点设置一个非负整数作为它的权值。对于 \(1 \le i \le n\)，若结点 \(i\) 的权值为 \(a_i\)，令 \(S_i\) 表示结点 \(i\) 的子树中结点权值构成的集合。对于每一种权值设置方案，定义树的价值为 \(\sum_{i=1}^{n} \mathrm{mex}(S_i)\)，其中 \(\mathrm{mex}(S)\) 表示不在集合 \(S\) 中的最小非负整数。例如，在下图中，若设置 \(a_1 = 3\)，\(a_2 = 2\)，\(a_3 = a_4 = 0\)，\(a_5 = 1\)，则 \(S_1 = \{0,1,2,3\}\)，\(S_2 = \{0,1,2\}\)，\(S_3 = \{0\}\)，\(S_4 = \{0\}\)，\(S_5 = \{1\}\)，树的价值为 \(4 + 3 + 1 + 1 + 0 = 9\)。

图片

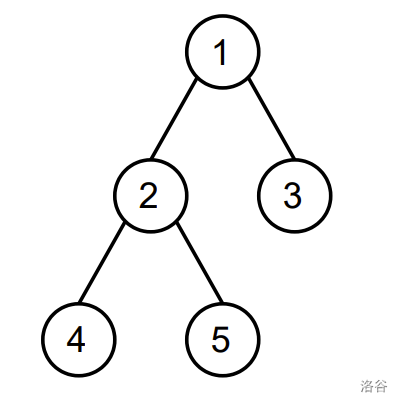
你需要求出，在所有权值设置方案中，树的价值的最大值。

输入格式

本题包含多组测试数据。

输入的第一行包含一个正整数 \(t\)，表示测试数据组数。

接下来依次输入每组测试数据，对于每组测试数据：

• 第一行包含两个正整数 \(n, m\)，分别表示结点数量与高度的上界。
• 第二行包含 \(n - 1\) 个正整数 \(p_2, p_3, \ldots, p_n\)，分别表示每个结点的父亲结点。

输出格式

对于每组测试数据，输出一行一个非负整数，表示树的价值的最大值。

输入输出样例 #1

输入 #1

2
5 2
1 1 2 2
7 2
1 1 2 2 2 3

输出 #1

9
13

说明/提示

【样例 1 解释】

该样例共包含两组测试数据。

对于第一组测试数据，可以设置 \(a_1 = 3\)，\(a_2 = 2\)，\(a_3 = a_4 = 0\)，\(a_5 = 1\)，则树的价值为 \(4 + 3 + 1 + 1 + 0 = 9\)。

对于第二组测试数据，可以设置 \(a_1 = 4\)，\(a_2 = 3\)，\(a_4 = 2\)，\(a_3 = a_6 = 1\)，\(a_5 = a_7 = 0\)，则树的价值为 \(5 + 4 + 2 + 0 + 1 + 0 + 1 = 13\)。

【样例 2】

见选手目录下的 tree/tree2.in 与 tree/tree2.ans。

该样例满足测试点 \(3,4\) 的约束条件。

【样例 3】

见选手目录下的 tree/tree3.in 与 tree/tree3.ans。

该样例满足测试点 \(7,8\) 的约束条件。

【样例 4】

见选手目录下的 tree/tree4.in 与 tree/tree4.ans。

该样例满足测试点 \(13,14\) 的约束条件。

【样例 5】

见选手目录下的 tree/tree5.in 与 tree/tree5.ans。

该样例满足测试点 \(18,19\) 的约束条件。

【数据范围】

对于所有测试数据，均有：

• \(1 \le t \le 5\)；
• \(2 \le n \le 8,000\)，\(1 \le m \le \min(n - 1, 800)\)；
• 对于所有 \(2 \le i \le n\)，均有 \(1 \le p_i \le i - 1\)；
• 给定的有根树的高度不超过 \(m\)。

测试点编号	\(n \le\)	\(m \le\)
\(1,2\)	\(7\)	\(n-1\)
\(3,4\)	\(13\)	^
\(5,6\)	\(18\)	^
\(7,8\)	\(40\)	^
\(9,10\)	\(120\)	^
\(11,12\)	\(360\)	^
\(13,14\)	\(4{,}000\)	\(2\)
\(15\sim 17\)	^	\(10\)
\(18,19\)	^	\(50\)
\(20\sim 25\)	\(8{,}000\)	\(800\)