Re:从零开始的斜率优化 DP 详解
update
点击查看详情
| 时间 | 修改 |
|---|---|
| 2025.7.26 | 改正“oi-wiki”拼写错误 |
斜率优化 DP 概述
斜率优化 DP 作为动态规划 DP 的重要优化手段,其核心思想源于数形结合与凸包理论的早期研究。虽然具体的“斜率优化” 术语在 21 世纪初随着算法竞赛的发展逐渐明确,但相关的优化思想可追溯至更早的数学与计算机科学领域。斜率优化的核心价值在于降低动态规划的时间复杂度。当 DP 转移方程中包含决策变量与当前变量的乘积项时,朴素解法需枚举所有可能决策,而斜率优化可实现优化。
前置知识
直线的方程
先看 百度百科。
直线的方程为一次函数,表达式一般为 \(y=kx+b\)。其中 \(k\) 为斜率,\(b\) 为截距。
凸包
定义一
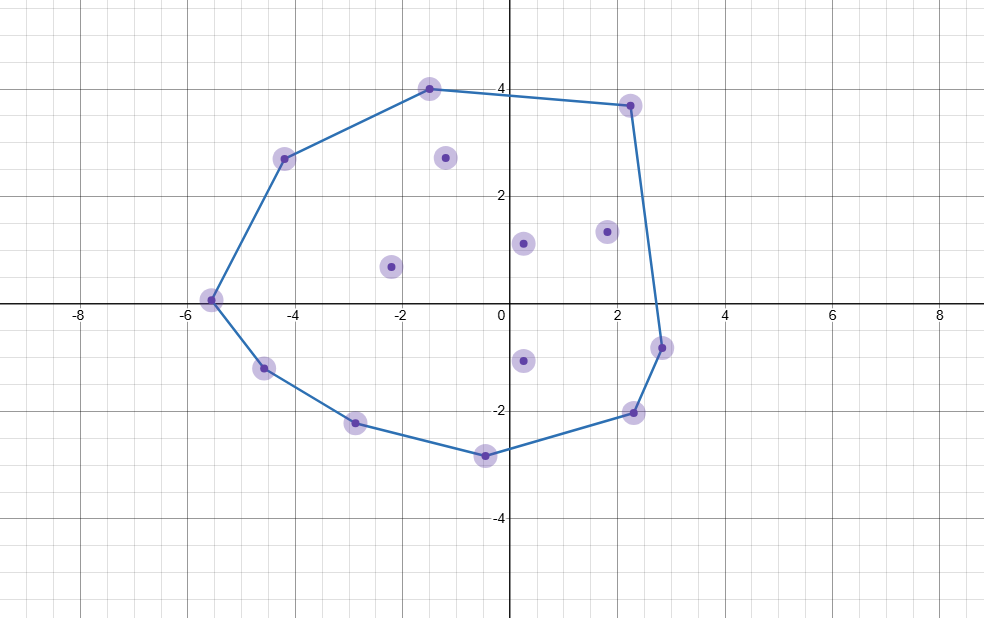
在平面上能包含所有给定点的最小凸多边形叫做凸包。
如图:
实际上可以理解为用一个橡皮筋包含住所有给定点的形态。
定义二
凸包中相邻的边若斜率愈来愈大则称下凸壳,相邻的边若斜率愈来愈小称上凸壳。
正文
本文会通过任务安排组题来学习斜率优化 DP。
任务安排 —— 前缀和优化 + 费用提前计算 DP
题面
题目描述
\(n\) 个任务排成一个序列在一台机器上等待完成(顺序不得改变),这 \(n\) 个任务被分成若干批,每批包含相邻的若干任务。
从零时刻开始,这些任务被分批加工,第 \(i\) 个任务单独完成所需的时间为 \(t_i\)。在每批任务开始前,机器需要启动时间 \(s\),而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。
每个任务的费用是它的完成时刻乘以一个费用系数 \(p_i\)。请确定一个分组方案,使得总费用最小。
输入格式
第一行一个正整数 \(n\)。
第二行是一个整数 \(s\)。
下面 \(n\) 行每行有一对数,分别为 \(t_i\) 和 \(p_i\),表示第 \(i\) 个任务单独完成所需的时间是 \(t_i\) 及其费用系数 \(p_i\)。
输出格式
一个数,最小的总费用。
输入输出样例 #1
输入 #1
5
1
1 3
3 2
4 3
2 3
1 4
输出 #1
153
说明 / 提示
【数据范围】
对于 \(100\%\) 的数据,\(1\le n \le 5000\),\(0 \le s \le 50\),\(1\le t_i,p_i \le 100\)。
【样例解释】
如果分组方案是 \(\{1,2\},\{3\},\{4,5\}\),则完成时间分别为 \(\{5,5,10,14,14\}\),费用 \(C=15+10+30+42+56\),总费用就是 \(153\)。
显然这是一道 DP 题,为防止题中 \(f\) 与递推数组名冲突规定其为 \(p\)。
解法 1
容易想到一个非常暴力的 DP。
\(f_{m,k}\) 表示前 \(i\) 个任务分成 \(j\) 组完成的最小代价。
初始化为 \(f_{m,k}=\left\{\begin{matrix} +\infty & m \ne 0 \vee k \ne 0\\ 0 & m = k = 0\end{matrix}\right.\)。
易得转移方程为 \(f_{i,j} = \min\limits_{1 \leq k \leq i} \left\{ f_{l-1,j-1} + \left(s + \sum_{l=k}^{i} t_l\right) \cdot \sum_{x=l}^{i} p_l\right\}\)。
其中几个求和函数可以使用前缀和维护。
设 \(st_m = \sum_{i=1}^mt_i\),\(sp_m = \sum_{i=1}^mp_i\)。
转移方程化为 \(f_{i,j} = \min\limits_{1 \leq k \leq i} \left\{ f_{l-1,j-1} + \left(s + st_k-st_{i-1}\right) \cdot (sp_k-sp_{i-1})\right\}\)。
时间复杂度:\(\Theta(n^3)\)。
解法 2
解法一已经无法再有明显的优化,考虑修改状态。
状态 \(f_{i,j}\) 中 \(j\) 只和以后的任务产生的代价有关,考虑去除这一维并提前计算。
设 \(f_i\) 表示处理前 \(i\) 个任务的最小总费用。
易得初始化为 \(f_m=\left\{\begin{matrix} +\infty & m \ne 0\\ 0 & m = 0\end{matrix}\right.\)。
考虑当 \(m = i\) 时如何转移。
枚举一个 \(j \le i\) 表示把 \(\left[j + 1, i\right]\) 划分为一批。
前 \(j\) 个任务完成最小代价为 \(f_j\),这一次分批所花费的代价 \(\sum_{k=1}^it_k\times\sum_{k=j+1}^np_i\),提前计算分批对之后的任务产生机器开机时间影响 \(s\times\sum_{i+1}^np_i\)。
由此,DP 转移式为 \(f_i=\min\limits_{0\le j\le i}\left\{f_j+\sum_{k=1}^it_k\times\sum_{k=j+1}^np_i+s\times\sum_{i+1}^np_i\right \}\)。
同样使用前缀和优化。
DP 转移式可化为 \(f_i=\min\limits_{0\le j\le i}\left\{f_j+st_i\times(sp_i-sp_j)+s\times(sp_n-sp_j)\right\}\)。
时间复杂度:\(\Theta(n^2)\)。
code
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e3 + 5;
int t[N], p[N], st[N], sp[N], f[N], n, s;
signed main() {
cin >> n >> s;
for (int i = 1; i <= n; i ++ ) cin >> t[i] >> p[i];
for (int i = 1; i <= n; i ++ )
st[i] = st[i - 1] + t[i],
sp[i] = sp[i - 1] + p[i];
memset(f, 0x3f, sizeof f); f[0] = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < i; j ++ )
f[i] = min(f[i], f[j] + s * (sp[n] - sp[j]) + st[i] * (sp[i] - sp[j]));
cout << f[n] << '\n';
return 0;
}
任务安排 2—— 斜率优化 DP(单调队列维护)
题面
题目背景
本题是 P2365 强化版,是 P5785 弱化版,用于让学生循序渐进地了解斜率优化 DP。
题目描述
机器上有 \(n\) 个需要处理的任务,它们构成了一个序列。这些任务被标号为 \(1\) 到 \(n\),因此序列的排列为 \(1 , 2 , 3 \cdots n\)。这 \(n\) 个任务被分成若干批,每批包含相邻的若干任务。从时刻 \(0\) 开始,这些任务被分批加工,第 \(i\) 个任务单独完成所需的时间是 \(T_i\)。在每批任务开始前,机器需要启动时间 \(s\),而完成这批任务所需的时间是各个任务需要时间的总和。
注意,同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 \(p_i\)。
请确定一个分组方案,使得总费用最小。
输入格式
第一行一个整数 \(n\)。第二行一个整数 \(s\)。
接下来 \(n\) 行,每行有一对整数,分别为 \(T_i\) 和 \(p_i\),表示第 \(i\) 个任务单独完成所需的时间是 \(T_i\) 及其费用系数 \(p_i\)。
输出格式
一行,一个整数,表示最小的总费用。
输入输出样例 #1
输入 #1
5
1
1 3
3 2
4 3
2 3
1 4
输出 #1
153
说明 / 提示
对于 \(100\%\) 数据,\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),\(1\le T_i \le 2^8\),\(0 \le p_i \le 2^8\)。
解题思路
题面与上题一模一样,但是 \(n\) 的范围扩大到了 \(3\times 10^5\)。
DP 的状态在上题中已经优化到了一维(最优),考虑优化转移。
对于方程 \(f_i=\min\limits_{0\le j\le i}\left\{f_j+st_i\times(sp_i-sp_j)+s\times(sp_n-sp_j)\right\}\),把 \(\min\) 函数扔到火星得:
展开得:
把 \(f_j\) 放到左边,\(f_i\) 放到右边得:
把与 \(i\) 有关或的和与 \(j\) 有关的分开得:
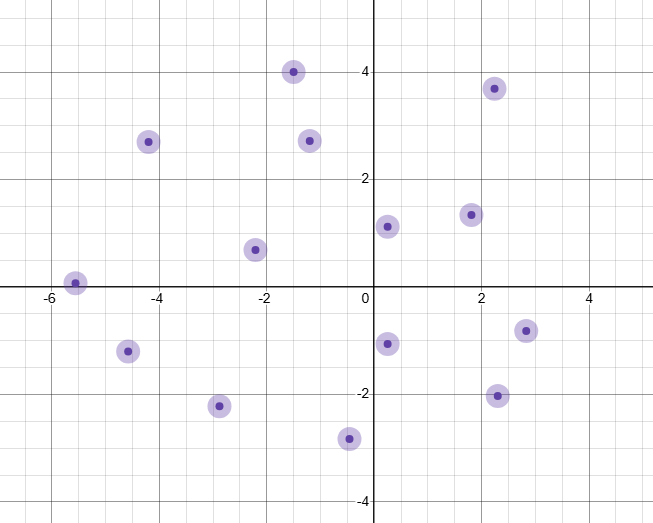
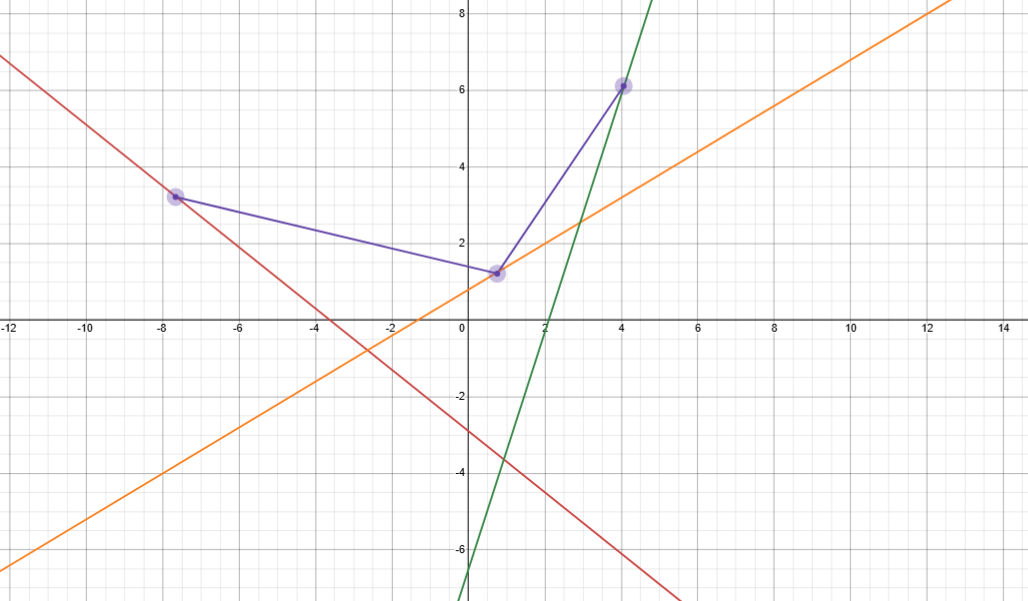
我们建立一个以 \(sp_j\) 为横坐标 \(f_j\) 为纵坐标,发现上式可看作一个以 \(st_i + s\) 为斜率,\(f_i-st_i\times sp_i-s\times sp_n\) 为截距的直线,对于每一种选择都对映了一个以 \(sp_j\) 为横坐标,\(f_j\) 为纵坐标的点,如下图所示:
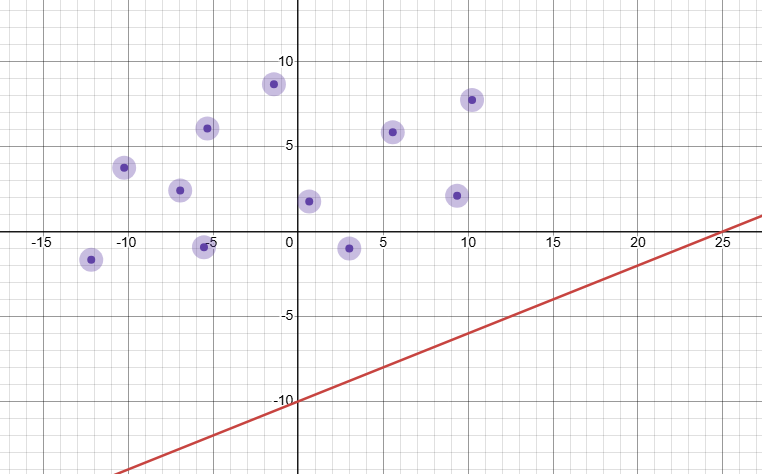
当 \(i\) 固定时,直线的斜率也是固定的,每当直线经过一点就可以得到一个截距,易发现截距最小时 \(f_i\) 也取到最小值。这说明直线从下向上运动到第一个点是就得到了最优解,如下:
我们来研究一下何时一个点有可能被取到。
考虑三个点如图形成一个上凸壳:
可以发现此时中间的点不可能被选到。
反之当三点形成如图一个下凸壳:
易发现此时中间的点可以取到。
所以我们只需要维护一个下凸壳即可。
设一二两点的连线的斜率为 \(k_1\),二三两点的连线斜率为 \(k_2\),进行决策的直线斜率为 \(K\)。
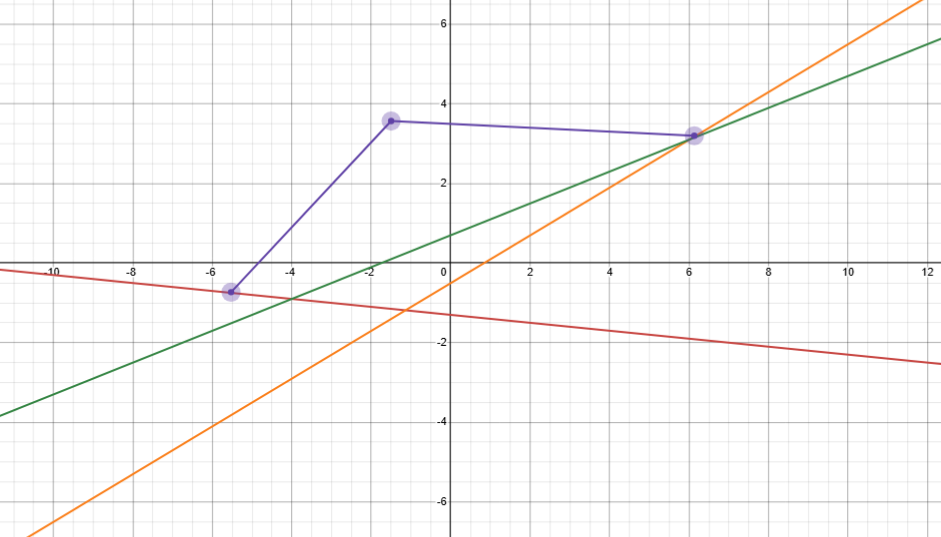
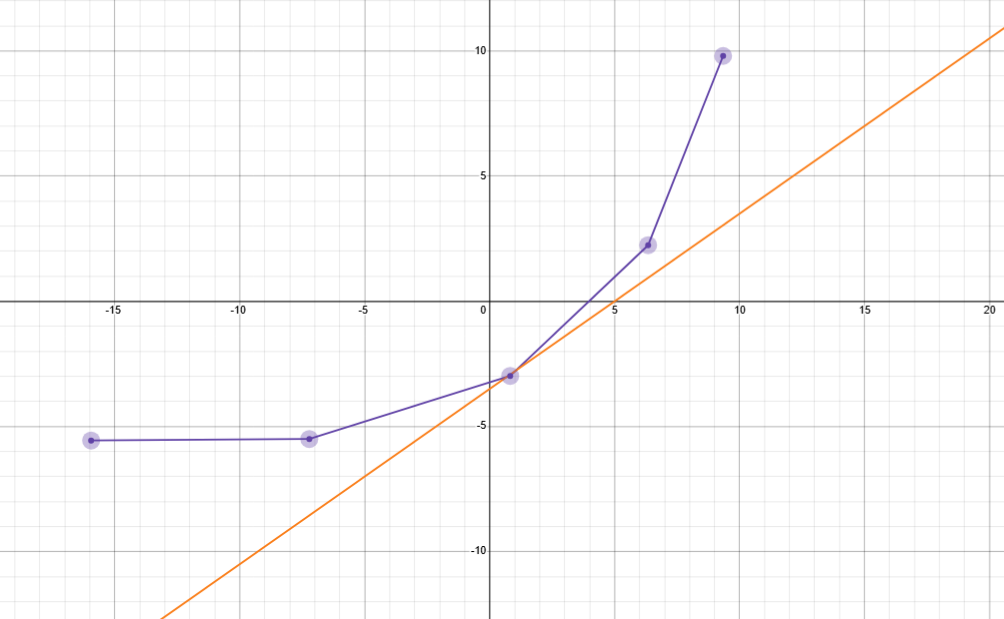
继续观察可以发现,一个点是最优解当且仅当 \(k_1 \le K \le k_2\)。简单来说若把决策的直线和所有凸包上的线段按斜率排序,则最优点就在直线该排的位置上,如图:
回到转移方程:\(f_i=\min\limits_{0\le j\le i}\left\{f_j+st_i\times(sp_i-sp_j)+s\times(sp_n-sp_j)\right\}\)。
和直线的方程:\(f_j=(st_i + s)sp_j+(f_i-st_i\times sp_i-s\times sp_n)\)。
这里 \(0\le j\le i\),所以当 \(i\) 增加时会有新的一个点加入。又因 \(sp\) 有单调性,故加入的点会在凸壳的最右端。由于只有在下凸壳中的点才可能最优,并且下凸壳中的线段斜率单调递增,故可以使用单调队列维护。又因为 \(st\) 单调递增(直线的斜率单调递增),凸包最右边的未选上的点不可能再被选上,所以把其弹出队列,队列最右端的点即为答案。
code
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 3e5 + 5;
int t[N], p[N], st[N], sp[N], f[N], n, s, q[N], l, r;
signed main() {
cin >> n >> s;
for (int i = 1; i <= n; i ++ ) cin >> t[i] >> p[i];
for (int i = 1; i <= n; i ++ )
st[i] = st[i - 1] + t[i],
sp[i] = sp[i - 1] + p[i];
memset(f, 0x3f, sizeof f); f[0] = 0; l = r = 1; q[1] = f[0];
for (int i = 1; i <= n; i ++ ) {
while (l < r && (f[q[l + 1]] - f[q[l]]) <= (s + st[i]) * (sp[q[l + 1]] - sp[q[l]])) l ++ ;
/*
(f[q[l + 1]] - f[q[l]]) <= (s + st[i]) * (sp[q[l + 1]] - sp[q[l]])
==> (f[q[l + 1]] - f[q[l]]) / (sp[q[l + 1]] - sp[q[l]]) <= s + st[i]
即最右侧两点形成线段的斜率小于当前决策斜率,右侧点不可能再被使用,弹出队列。
*/
int j = q[l];
f[i] = f[j] + s * (sp[n] - sp[j]) + st[i] * (sp[i] - sp[j]);
//f_i = f_j + st_i * (sp_i - sp_j) + s * (sp_n - sp_j)
while (l < r && (f[q[r]] - f[q[r - 1]]) * (sp[i] - sp[q[r]]) >= (f[i] - f[q[r]]) * (sp[q[r]] - sp[q[r - 1]]))
r -- ;
/*
(f[q[r]] - f[q[r - 1]]) * (sp[i] - sp[q[r]]) >= (f[i] - f[q[r]]) * (sp[q[r]] - sp[q[r - 1]])
==> (f[q[r]] - f[q[r - 1]]) / (sp[q[r]] - sp[q[r - 1]]) >= (f[i] - f[q[r]]) / (sp[i] - sp[q[r]])
维护单调队列中斜率的单调性
*/
q[++ r] = i;
}
cout << f[n] << '\n';
return 0;
}
[ZJOI2010] 任务安排——斜率优化 DP(单调栈 + 二分维护)
题面
题目描述
机器上有 \(n\) 个需要处理的任务,它们构成了一个序列。这些任务被标号为 \(1\) 到 \(n\),因此序列的排列为 \(1 , 2 , 3 \cdots n\)。这 \(n\) 个任务被分成若干批,每批包含相邻的若干任务。从时刻 \(0\) 开始,这些任务被分批加工,第 \(i\) 个任务单独完成所需的时间是 \(T_i\)。在每批任务开始前,机器需要启动时间 \(s\),而完成这批任务所需的时间是各个任务需要时间的总和。
注意,同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)。
请确定一个分组方案,使得总费用最小。
输入格式
第一行一个整数 \(n\)。
第二行一个整数 \(s\)。
接下来 \(n\) 行,每行有一对整数,分别为 \(T_i\) 和 \(C_i\),表示第 \(i\) 个任务单独完成所需的时间是 \(T_i\) 及其费用系数 \(C_i\)。
输出格式
一行,一个整数,表示最小的总费用。
输入输出样例 #1
输入 #1
5
1
1 3
3 2
4 3
2 3
1 4
输出 #1
153
说明/提示
对于 \(100\%\) 数据,\(1 \le n \le 3 \times 10^5\),\(1 \le s \le 2^8\),$ \left| T_i \right| \le 2^8$,\(0 \le C_i \le 2^8\)。
题目思路
这道题的题面还与上道题相同,但是 \(\left| T_i \right| \le 2^8\),所以 \(st\) 不具有单调性。
\(st\) 无单调性会产生什么影响呢?
看直线方程:\(f_j=(st_i + s)sp_j+(f_i-st_i\times sp_i-s\times sp_n)\)。
这说明直线的斜率不具有单调性。
怎么办呢?我们用一个单调栈维护整个下凸壳,可以发现单调栈内的斜率是递增的。我们每次二分出最后个比决策直线斜率小的线段,其右端点即为答案。
证明参考:一个点是最优解当且仅当 \(k_1 \le K \le k_2\)。
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 3e5 + 5;
int t[N], p[N], st[N], sp[N], f[N], n, s, top, sta[N];
int search(int i) {
int l = 1, r = top, ans = 0;
while (l <= r) {
int mid = (l + r) >> 1, a = sta[mid - 1], b = sta[mid];
if (f[b] - f[a] <= (st[i] + s) * (sp[b] - sp[a]))
l = mid + 1, ans = mid;
else r = mid - 1;
}
return sta[ans];
}
signed main() {
cin >> n >> s;
for (int i = 1; i <= n; i ++ ) cin >> t[i] >> p[i];
for (int i = 1; i <= n; i ++ )
st[i] = st[i - 1] + t[i],
sp[i] = sp[i - 1] + p[i];
memset(f, 0x3f, sizeof f); sta[top = 1] = f[0] = 0;
for (int i = 1; i <= n; i ++ ) {
int j = search(i);
f[i] = f[j] + s * (sp[n] - sp[j]) + st[i] * (sp[i] - sp[j]);
while (top > 1 && (f[sta[top]] - f[sta[top - 1]]) * (sp[i] - sp[sta[top]]) >= (f[i] - f[sta[top]]) * (sp[sta[top]] - sp[sta[top - 1]]))
top -- ;
sta[++ top] = i;
}
cout << f[n] << '\n';
return 0;
}
补
此章仅讨论了 DP 方程中判断函数为 \(\min\) 的情况,当函数为 \(\max\) 时只需决策直线从向上靠近决策点变成向下靠近,所以维护上凸壳即可。
习题
两项单调
都不单调
P4655 [CEOI 2017] Building Bridges - 洛谷


 浙公网安备 33010602011771号
浙公网安备 33010602011771号