「ARC_172_A_Chocolate」题解

题意

给定一 \(h\times w\) 大小的巧克力，从中分下 \(n\) 块，第 \(i\) 块大小为 \(2^{a_i}\times 2^{a_i}\) 的正方形，问能否成功分（允许原巧克力有剩余）。

• \(1\leq h\leq 10^9\)
• \(1\leq w\leq 10^9\)
• \(1\leq n\leq 1000\)
• \(0\leq a_i\leq 25\)
• 题目链接

解法

采取贪心做法。

将 \(a_i\) 从大到小排序，防止分的太凌乱无法继续分大块。

对于每一次分，取剩余所有块中最大的一块（此处最大指的是 \(\min(x,y)\) 最大，\(x,y\) 表示长和宽）。

对于这一块，如果能继续分当前块，设 \(s=2^{a_i}\) ，则若 \(x>=s\) 且 \(y>=s\) ，则可分出该块。

分出该块后，将其剩余部分继续分成两块，并存起来，如下图：

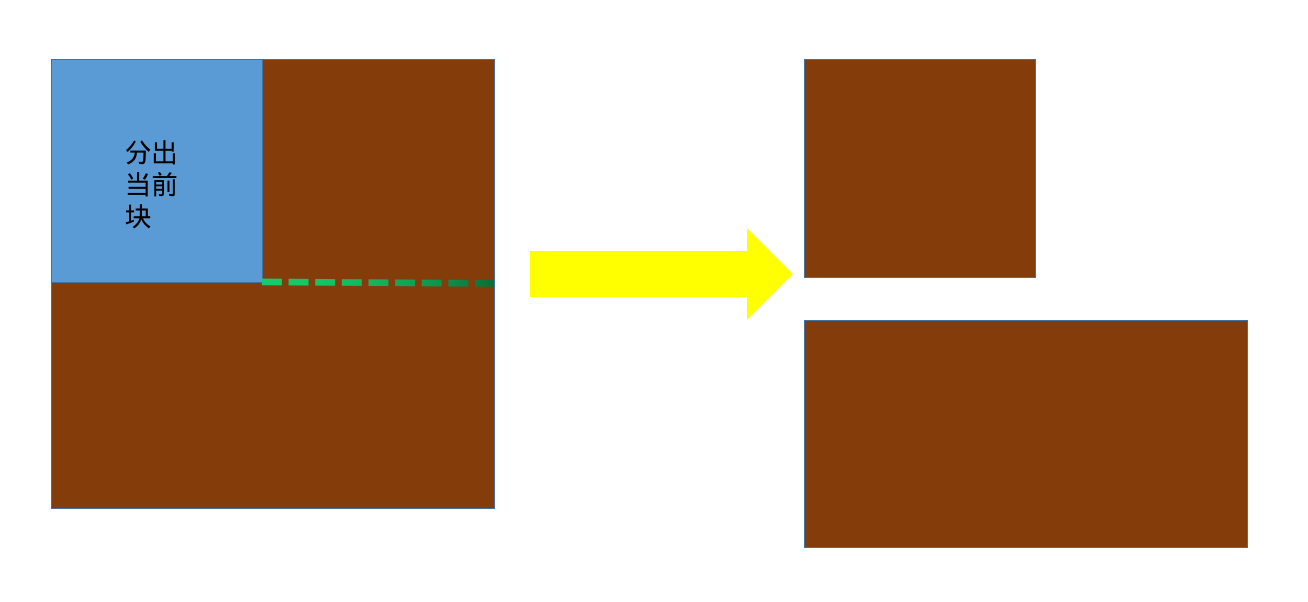
这里可以采用大根堆，当然也可以用数组，但数组的话就要每次从大到小排序，不过也不会超时，数据不大，主要用大根堆的话不好处理他按什么排序。

把新割出来的两块压进去，重复该操作即可。

至于这么割会不会漏情况，由于我们是从大到小排序的，实际上不管横着还是竖着割，都是相差不大的，而且割出来的两个块一定是足够大的。我们每次都取最大的一块割，如果这都不行，那一定是不行。

如果能割到最后，就是 \(Yes\) ，中间没法继续割了的话输出 \(No\) 结束运行就可以了。

代码

#include<bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
const int N=101000,P=1e9;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool z=1;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(z?x:~x+1);
}
int h,w,n,a[N],sum,cnt;
struct aa
{
    int x,y;
}q[N];
bool cmp(aa a,aa b) 
{
    int x=min(a.x,a.y),y=min(a.x,a.y);
    return x>y;
}
bool dmp(int a,int b) {return a>b;}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
    read(h),read(w),read(n);
    q[++cnt].x=h,q[cnt].y=w;
    for(int i=1;i<=n;i++) read(a[i]),sum+=powl(2,a[i]);
    if(h*w<sum) cout<<"No",exit(0);
    stable_sort(a+1,a+1+n,dmp);
    for(int i=1;i<=n;i++)
    {
        stable_sort(q+1,q+1+cnt,cmp);
        int s=powl(2,a[i]),flag=0;
        for(int j=1;j<=cnt;j++)//此处实际上只进行1次，因为排序了。
            if(q[j].x>=s&&q[j].y>=s)
            {
                int x=q[j].x,y=q[j].y;
                q[j].x=0,q[j].y=0;
                q[++cnt].x=s,q[cnt].y=y-s,
                q[++cnt].x=x-s,q[cnt].y=y;
                flag=1;
                break;
            }
        if(!flag) cout<<"No",exit(0);
    }
    cout<<"Yes";
}