OO第一次作业
第一次作业
1.作业思路
第一次作业的需求较少,仅仅是针对一元多项式的求导,而且由于是第一次接触类的建立与使用,并且没有考虑到任务的可拓展性,我是按照以前写代码的风格用过程性语言的风格完成的第一次作业。
2.数据结构
针对第一次作业中的提示,我使用的是两个动态数组来管理每个项的系数与幂指数,这样方便合并和化简,并且为了能够处理超大数的问题,我使用了BigInteger类型来进行数据管理。
private ArrayList<BigInteger> listMi = new ArrayList<BigInteger>();
private ArrayList<BigInteger> listXiShu = new ArrayList<BigInteger>();
3.代码实现
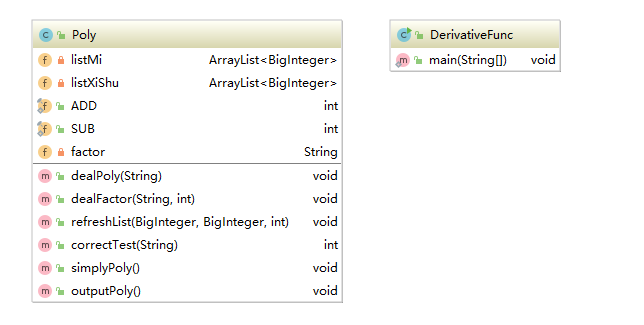
我仅仅使用了两个类,DerivativeFunc是主函数,里面只是实例化了Poly类,并且调用其中的方法,以此达到对多项式求导的目的。
- correctTest():是使用了正则表达式对输入串进行模式匹配,验证输入串的正确性的
- dealPoly():和dealFactor分别是将输入串表达式分解成项以及对项进行求导处理
- refreshList():用来将求导后的结果插入到listMi与listXiShu两个arrayList中
- simplyPoly():用来对结果表达式进行化简
- outputPoly():用来将结果按照格式正确输出。
4.代码分析

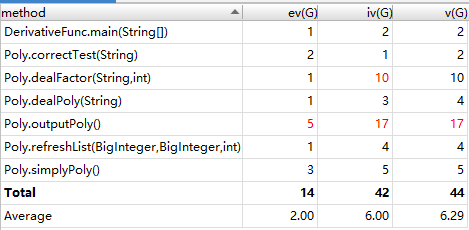
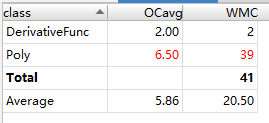
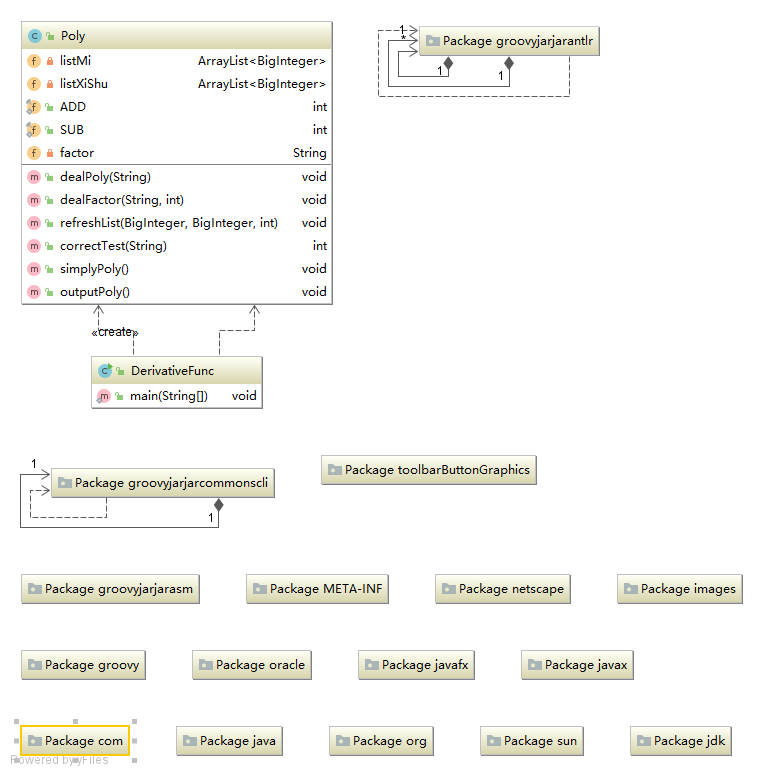
5.BUG发现
对bug的查找和修复主要是自己针对极端情况编写测试代码,在公测中没有出现错误。
6.编写测试程序
我第一次作业中对于测试程序的编写主要是针对WRONG FORMAT进行测试,比如缺少符号或带符号整数中+-与数字被分隔开等等,还有对正确性的测试,例如输入为空,为0,为超大数等极端情况等。
7.结果的简化
第一次作业的结果简化主要是进行了合并同类项。
第二次作业
1.作业思路
本次作业提高了难度,增加了两个三角函数Sin(x)与Cos(x),很明显能够看到,第一次设计的架构已经完全不能支撑这一次作业的编写了,如果仅仅仿照第一次作业的思路,用arrayList继续存储Sin(x)与Cos(x)的系数、幂指数,那么对于代码的扩展将十分不利,因此我采用了HashMap,Key类型为我自己编写的类Term,Value类型为BigInteger用来存储对应项的系数,在guideBook的指导下,我重新编写了equal()与hashCode()方法。
private HashMap<Term, BigInteger> hash = new HashMap<>();
2.数据结构
在Expression类中,使用 HashMap<Term, BigInteger>来对项进行统一管理。
在Term类中,有四个private变量,分别存储这个项的x幂指数、sin(x)幂指数、cos(x)幂指数以及这个项的系数
private BigInteger xxMi; private BigInteger siMi; private BigInteger cosMi; private BigInteger xiShu;
3.代码实现
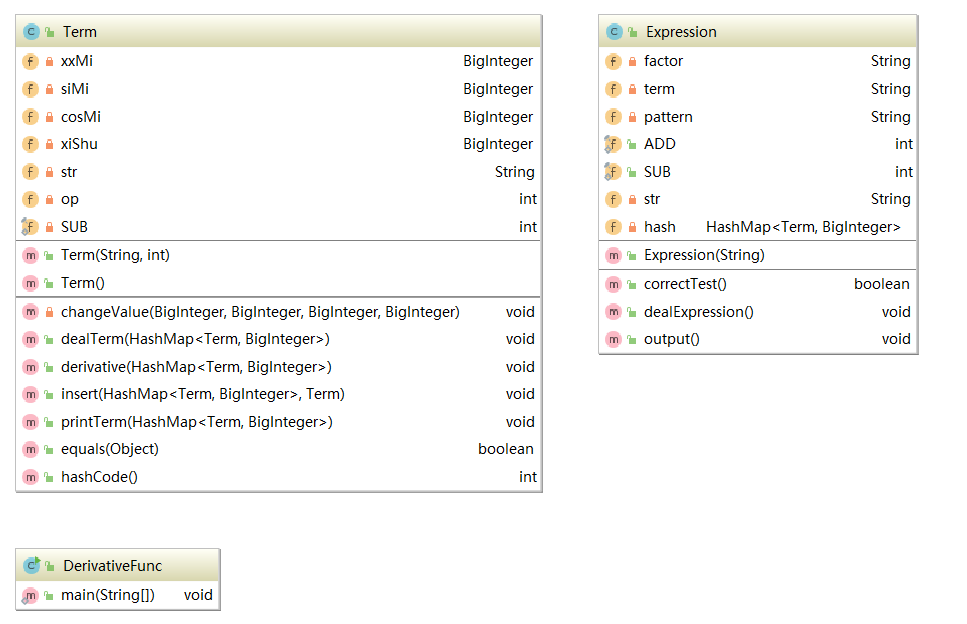
Expression class中:
- correctTest()用来对输入串进行正确性检测
- dealExpression()用来将表达式拆分成若干项
- output()用来将结果按照正确格式输出
Term class中:
- dealTerm()用来处理当前项
- derivative()用来对当前项进行求导
- insert()用来将求导后的结果插入到hashMap中
- printTerm()用来打印结果项
- equals()为重构的方法
- hashCode()为重构的方法
4.代码分析

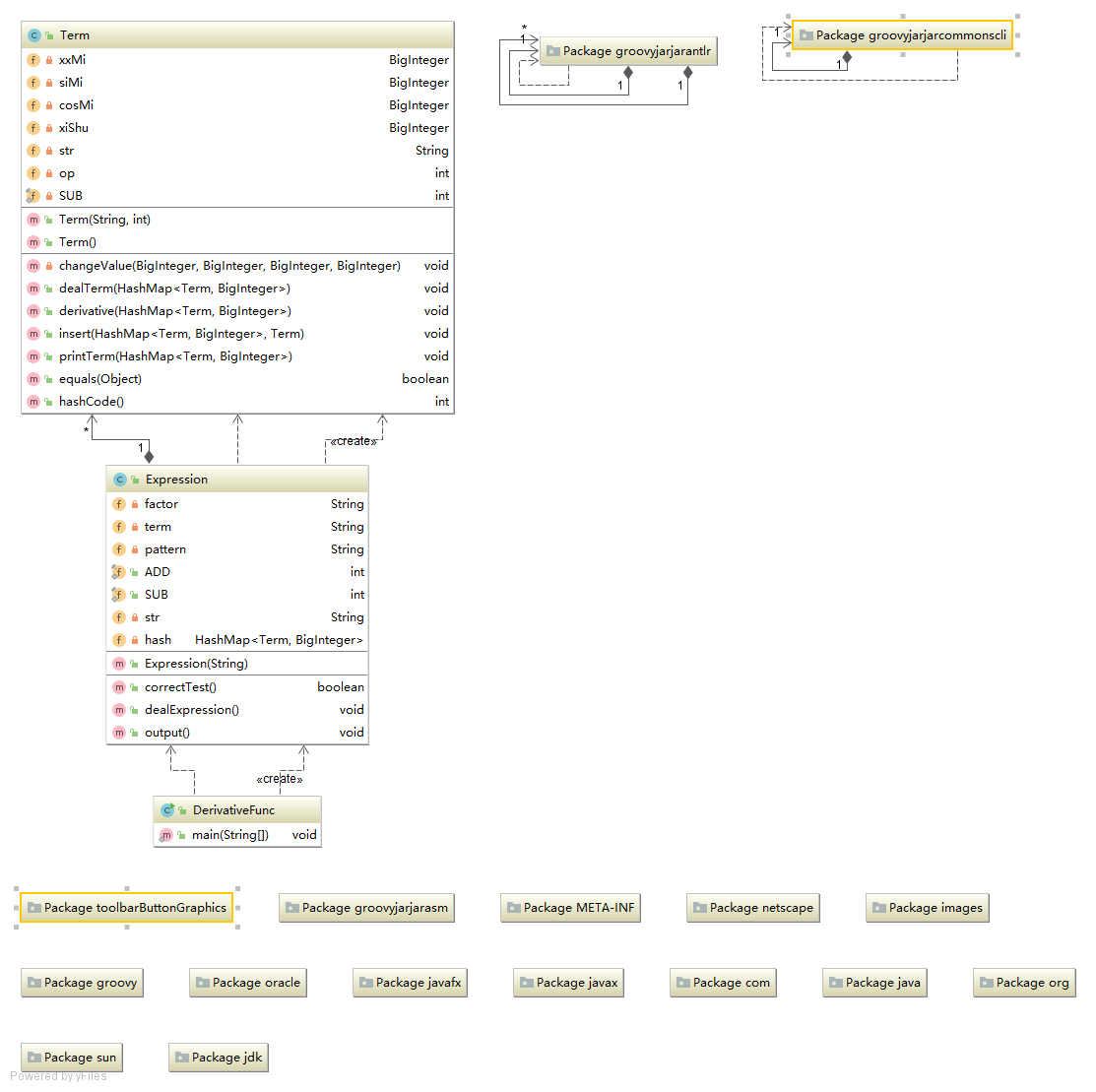
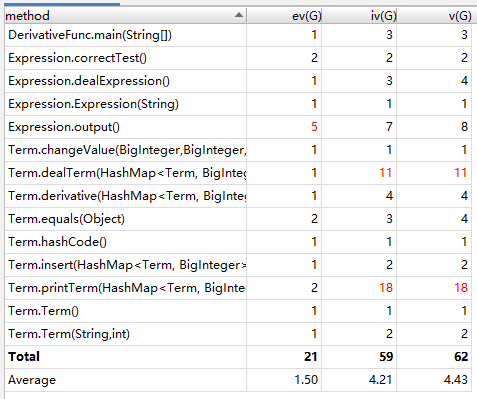
5.BUG发现
对BUG的查找主要是对极端情况的测试,公测没有出现bug。
6.编写测试程序
我第一次作业中对于测试程序的编写主要是针对WRONG FORMAT进行测试,比如缺少符号或带符号整数中+-与数字被分隔开,sin(x)\cos(x)格式不正确等等,还有对正确性的测试,例如输入为空,为0,为超大数等极端情况等。
7.结果的简化
这一次作业中,我所做的简化一是仿照第一次作业进行同类项合并,二是对三角函数进行简化,例如sin(x)^2+cos(x)^2=1。
对三角函数的优化我分为了两类:
- k*sin(x)^(i+2)*cos(x)^i + k*cos(x)^(i+2)*sin(x)^i = k*cos(x)^i*sin(x)^i,这是sin(x)^2与cos(x)^2系数相等的情况,我会将它们进行合并
- k*sin(x)^(i+2)*cos(x)^i + m*cos(x)^(i+2)*sin(x)^i = (k-m)*sin(x)^(i+2)*cos(x)^i + m*cos(x)^i*sin(x)^i,其中k>m,对于这种情况,化简后的结果相较于化简前的结果,有可能出现长度增加的情况,于是我会查找hashMap中是否包含有cos(x)^i*sin(x)^i这一项,如果包含这一项,那么就一定能够保证化简后的长度小于化简前的长度,达到了化简的目的(因为可以将m*cos(x)^i*sin(x)^i进行合并同类项,减少了len(m*cos(x)^(i+2)*sin(x)^i)长度)。
第三次作业
1.作业思路
这一次的作业难度陡然上升,虽然在作业二的时候已经有考虑到下一次作业的难度升级,并且在第二次作业的架构上也考虑到了,但上一次没有用链式求导法进行求导,显然上一次的架构已经完全不适合现在的作业要求了。这一次作业很明显需要完完全全按照链式求导法进行求导,否则极其容易出现错误,并且不容易实现代码。简单分析一下,我发现共有四种因子:x、sin()、cos()、表达式因子,因此我为创建了这四种类,其中sin()和cos()类中会实例化一个表达式因子类,除此之外,我还建立了一个表达式类以及项类。每一种类都有一个求导方法,并且这个求导方法会向调用者返回一个字符串string,这个string就是这个因子、项、表达式求导后的结果,依照这个思路,我开始编写代码。
2.数据结构
在Expression类中有一个ArrayList<Term>用来存储项。
在Term类中有一个Method类型的ArrayList,这个ArrayList为一个接口,因为需要统一管理四种不同的因子,所以这四种因子类都需要有一个相同的接口,以此才能在Term类中对不同类的因子统一管理。
private ArrayList<Method> list = new ArrayList<Method>();
3.代码实现
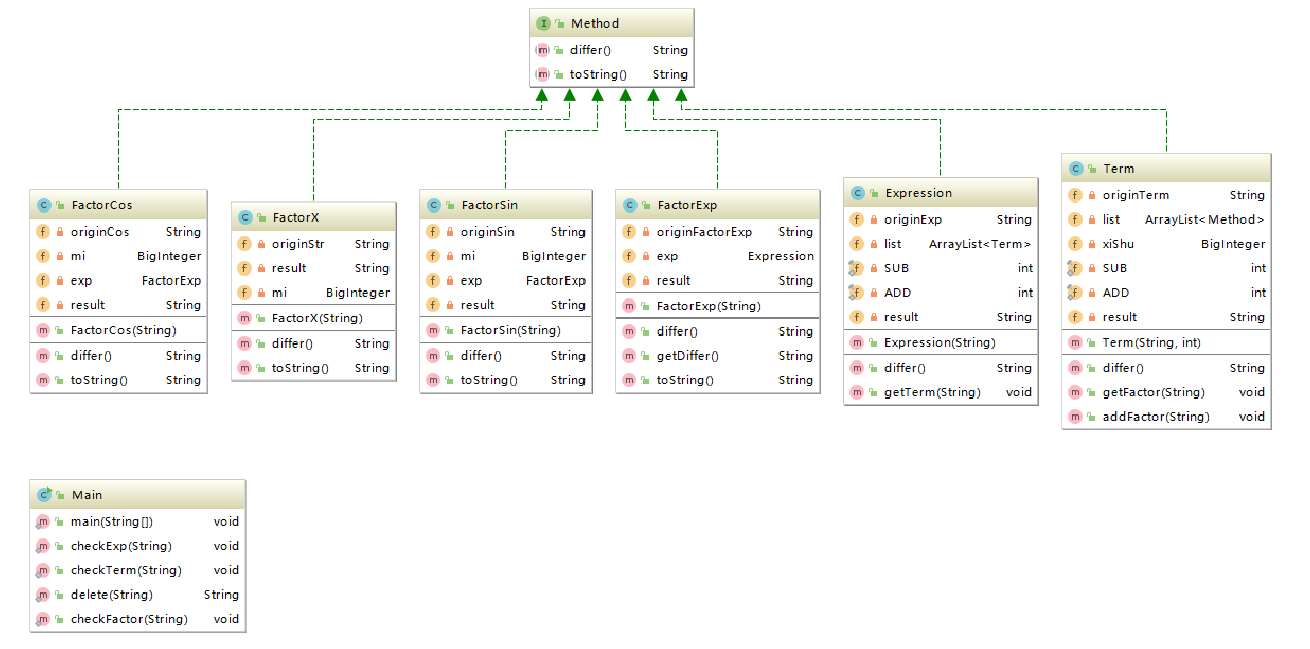
Method Interface中:
- differ()为求导方法
- toString()为将求导后的结果按正确格式转换为字符串
Main class中:
- checkExp\checkTerm\checkFactor为验证输入串的正确性的方法
- delete()为一个删除括号的方法,用来辅助验证表达式因子的正确性
FactorCos\FactorX\FactorSin\FactorExp class中:
- differ()为因子的求导方法
- toString()为将求导后的结果按正确格式转换为字符串
Expression class中:
- differ()为表达式的求导方法
- getTerm()为将表达式拆分为若干个项,并且实例化若干个Term对象
Term class中:
- differ()为项的求导方法
- getFactor()为将项拆分为若干个因子,并且调用addFactor()方法实例化若干个因子
- addFactor()实例化若干个因子
4.代码分析

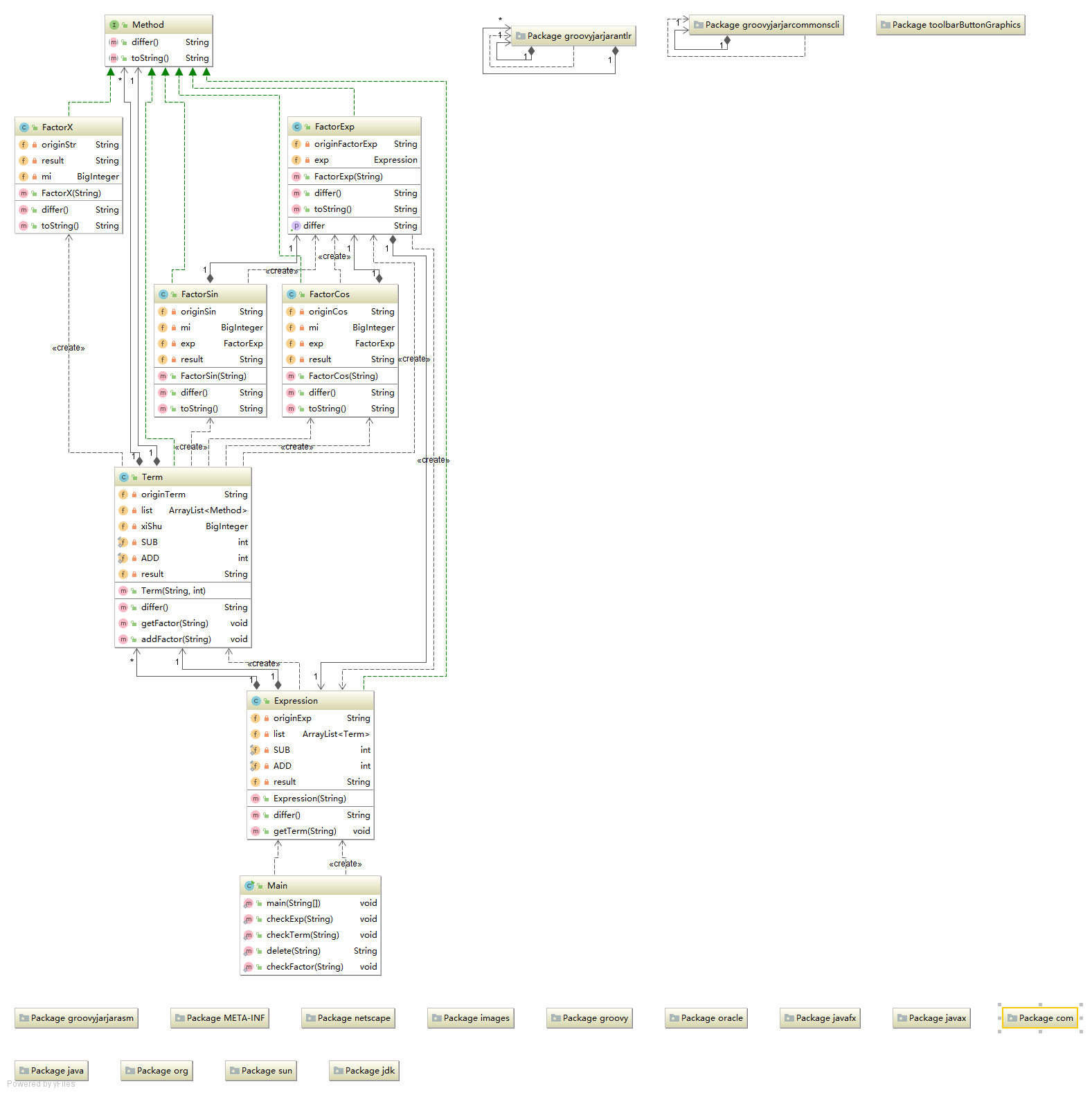
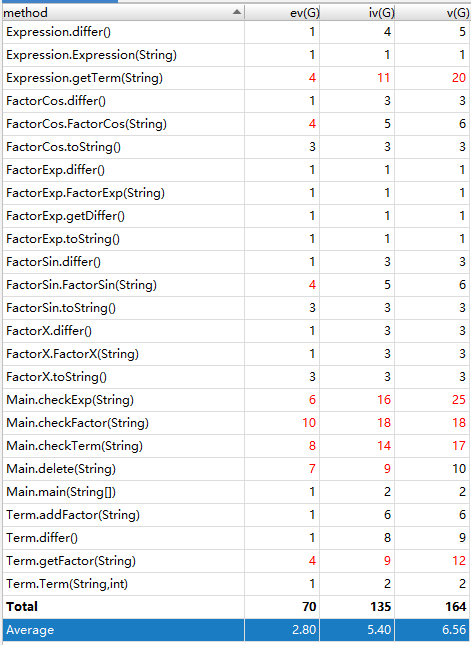
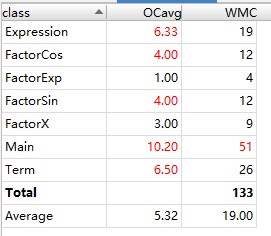
5.BUG发现
公测中有一个出现了一个错误,对于这个输入串没有判断出是WRONG FORMAT,我的众多测试中测试了各种错误,唯独忽略了多一个*号的错误,在此十分懊悔,在对输入串可能表达式少括号、多括号、sin中出现空格\t的验证颇多,对正确性也进行了大量测试,万万没想到在这么一个明显的错误上翻了车。现在分析看来,主要是由于采用的递归下降分析法依照编译原理的思路来验证输入串的正确性的,因此正确性的验证十分麻烦,忽略了对*的正确性判断,以后要加强对显而易见出现的bug进行测试!
2 * (sin(x)) *(x)*sin((x))^+1*x*cos(x)^+2*cos(x)*(((x)))*-1*
6.编写测试程序
我第一次作业中对于测试程序的编写主要是针对WRONG FORMAT进行测试,比如缺少符号或带符号整数中+-与数字被分隔开,sin(x)\cos(x)格式不正确等等,还有对正确性的测试,例如输入为空,为0,为超大数等极端情况等。 由于这一次求导较难,于是我的注意力主要集中在对程序进行正确性的验证上,却忽略了一个最明显的bug,真是太不应该了!
7.结果的简化
这一次作业的结果简化有很多可以做,比如表达式有连续多个括号嵌套:(((1+x))),可以将括号减少至一层,还可以进行同类项的合并等。我在这一次作业中,一开始做了很多的化简,将项中的因子合并:3*4*x^3*sin(x)*x化简为12*x^4*sin(x),可以将表达式多层括号嵌套化简:3*(((1+x)))*sin(((x+2)))化简为3*(1+x)*sin(x+2),但是在ddl前发现一个化简Bug,对于括号的化简有问题:(3+x)*3会化简为3+x)*,这很明显是括号的结束没有判断准确,我迅速定位到了这个bug,然后将其改正,但是随后又找到了对于一个表达式嵌套的化简存在Bug,这一次我找了很久也没有找到bug,时间也快到了ddl,不敢抱有侥幸心理,我将没有化简的程序交了上去,使得最终的性能分都是0分...
总结
1.架构与模式
第二次作业没有用第一次作业的架构,因为第二次作业增加了两个三角函数,如果用第一次的架构,将使用4个ArrayList进行操作,这将非常复杂,而且也不利于程序功能的扩展,于是我第二次完全重新写了一个架构。
第三次作业没有用第二次作业的架构,因为sin(x)和cos(x)会嵌套表达式因子,这导致第二次的hashMap也不够用了,于是我重新写了一个新的链式求导的架构。
第三次作业的模式属于工厂模式,通过实例化相同接口下的类来做到对它们的统一管理。
2.感想与收获
第一次作业完全不熟悉面向对象解决问题的思路,基本上是按照面向过程来解决问题的,调用一个一个的方法在同一个类中解决所有问题,到了第二次第三次情况有所改善,能够做到将需要解决的问题进行抽象化,上升到一个类的层面,通过建造不同的类来达到解决问题的目的,这也使得程序有着更高的可扩展性。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号