线性表
线性表的定义:由n个具有相同类型的数据元素的有限序列。(n为线性表的长度,n=0则为空表,n!=0则为非空表);
- 线性表的特征:
- 同一性:线性表由相同类型的数据元素组成,每个元素属于同一数据对象。
- 有限性:线性表是由有限个数据元素组成,表中数据元素的个数就是表的长度。
- 有序性:线性表中相邻的数据元素之间存在序偶关系。
- 线性表的顺序表示与实现
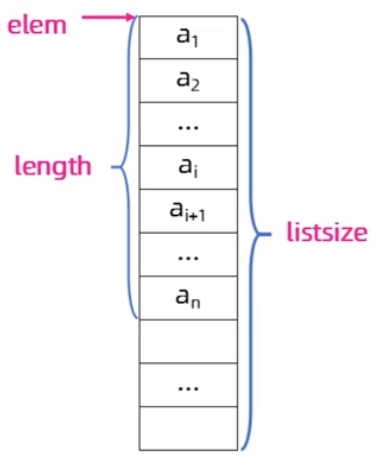
- 定义:用一组地址连续的存储单元依次放线性表中的各个元素。线性表的顺序表示可以简称为顺序表。
- 顺序表的C语言表示。
-
#define LIST_INIT_SIZE 100 #define LISTINCREMENT 10 typedef struct { ElemType *elem; int length;//表的长度 int listsize;//分配的容量 }SqList
-
顺序表的建立
Status InitList_Sq(SqList &L){ //构造一个空的线性表 L.elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType)); if(!elem)exit(OVERFLOW); L.length=0; L.listsize=LIST_INTI_SIZE; return OK; }
Status InitList_Sq(SqList &L){ //构造一个非空的线性表 L.elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType)); if(!elem)exit(OVERFLOW); cin<<n; for(int i=0;i<n;i++) cin>>L.elem[i]; L.length=n; L.listsize=LIST_INTI_SIZE; return OK; }
- 顺序表的输出
Status OutPut_Sq(SqList L){ for(int i=0;i<n;i++){ cout<<L.elem[i]; } }
- 顺序表求表长
int ListLength(SqList L) { return L.length; }
- 顺序表的查找
1、按值查找 int LocateList(SqList L,ElemType e){ int i=1; for(i=1;i<=L.length&&L.elem[i]!=e;i++); if(L.length>i)return i; else return 0; }
算法的时间复杂度为O(n);2.按位查找
Status GetList(SqList L,int i;ElemType &e){
if(i<1||i>L.length)return ERROR;//验证i的合理性
e=L.elem[i-1];
return OK;
}
时间复杂度为O(1); - 顺序表的插入
Status ListInsert(SqList L,int i,ElemType e){ if(i<1||i>L.length) return ERROR; if(L.length>=L.listsize){ newbase=(ElemType*)realloc(L.elem, (L.listsize+LISTINCREMENT)*sizeof(ElemType)); if(!newbase)exit(OVERFLOW); L.elem=newbase; L.listsize+=LISTINCREMENT; } p=&(L.elem[i-1]);//取地址 for(int j=&(L.elem(L.length-1));j>=p;j--) *(j+1)=*(p);//通过*使得值相等 *p=e;
return OK; } 时间复杂度:最好:O(1);最坏:O(n);平均:O(n); - 顺序表的删除
Status ListDelete(SqList L,int i;ElemType &e){ if(i<1||i>L.length) return ERROR; p=&(L.elem[i-1]); e=*p; q=L.elem+L.length-1; for(++p;p<=q;++p) *(p-1)=*(p); --L.length; return OK; }
时间复杂度:最好:O(1);最坏:O(n);平均:O(n);
-
- 线性表的链式表示与实现
- 单链表*
- 定义:用一组任意单元,分别来存储线性表中的元素。
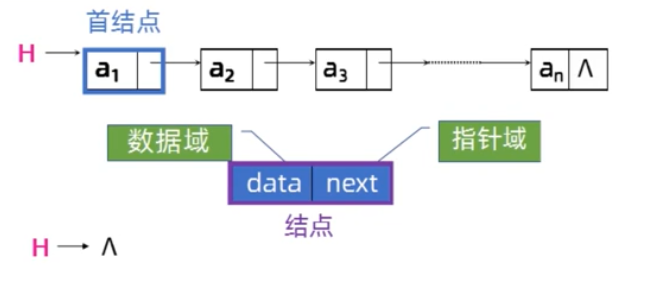
设置头结点(为了使插入和删除操作统一,在插入和删除第一个结点时不需另作判断;无论链表是否为空,头指针始终指向头结点)


- 单链表的C语言表示
-
typedef struct LNode{ ElemType data; struct LNode *next;//指针,指向后继结点地址 }LNode,*Linklist;//LNode是结点类型,LinkList是结构指针类型
- 单链表的建立
1.空表 Status InitList(LinkList &L){ L=(LinkList)malloc(sizeof(LNode)); if(!L)exit(OVERFLOW); L->next=NULL; }
2.头插法建立非空链表(输入与输出结果是相反的) Status InitList(LinkList &L){ L=(LinkList)malloc(sizeof(LNode)); if(!L)exit(OVERFLOW); L->next=NULL; cin>>n; for(int i=0;i<n;i++){ LinkList p=(LinkList)malloc(sizeof(LNode)); cin>>p->data; p->next=L->next; L->next=p; } return OK; }
3、尾插法建立非空链表(输入结果与输出结果一致) Status InitList(LinkList &L){ L=(LinkList)malloc(sizeof(LNode)); if(!L)exit(OVERFLOW); L->next=NULL;LinkList q=L; cin>>n; for(int i=0;i<n;i++){ LinkList p=(LinkList)malloc(sizeof(LNode)); cin>>p->data; q->next=p; q=p; } q->next=NULL; return OK; }
- 链表的输出
void OutPut(LinkList L){ LinkList p=L; while(p){ cout<<p->data; p=p->next; } }
- 求单链表的长度
int ListLength(LinkList L){ int i=0; LinkList p=L->next; while(p){ i++; p=p->next; } return i; }
- 单链表的查找
1.按值查找 LinkList LocateElem(LinkList L,ElemType e){ LinkList p=L->next; while(p){ if(p->data==e) return p; p=p->next; } return NULL; }
算法时间复杂度为O(n)2.按位置查找 Status GetElem(LinkList L,int i,ElemType &e){ LinkList p=L->next; for(int j=1;p&&j<i;j++;p=p->next) ; if(!p||j>i)return ERROR; e=p->data; return OK; } 算法的时间复杂度为O(n)
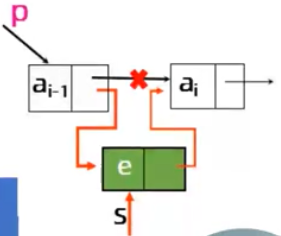
- 单链表的插入
Status InsertList(LinkList &L,int i,ElemType e){ LinkList p=L; int j=0; while(p&&j<i-1){ p=p->next; j++; } if(j>i-1||!p) return ERROR; s=(LinkList)malloc(sizeof(LNode)); s->data=e; s->next=p->next; p->next=s; return OK; } 时间复杂度为O(n)
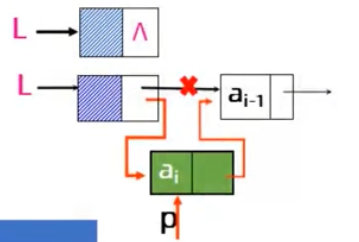
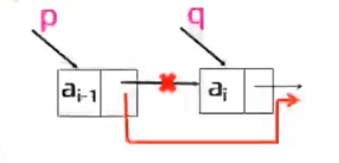
- 单链表的删除
Status DeleteList(LinkList &L,int i,ElemType &e){ LinkList p=L; int j=0; while(p->next&&j<i-1){ if(!p->next||j>i-1) return ERROR; q=p->next; e=q->data; p->next=q->next; free(q); return OK; } 时间复杂度为O(n);
-
- 定义:用一组任意单元,分别来存储线性表中的元素。
- 循环链表
- 定义:收尾相连的链表。
- 结构:将单链表尾结点的指针域指向头结点。
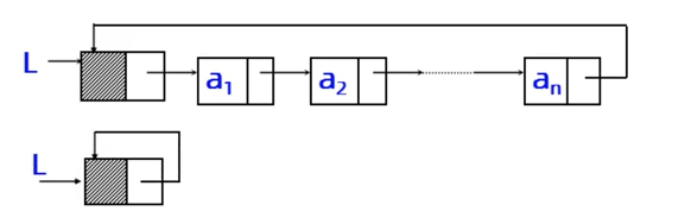
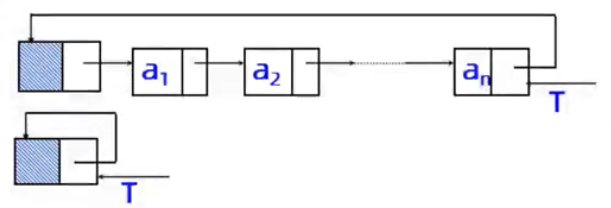
- 特点:表中所有结点都链在一个环上;可以从任何结点出发,沿着一个方向,访问表中所有结点。
- 循环链表判空条件:L->next==L;尾结点p的判断方法:p->next==L;
- 循环链表的合并:
- 带头指针(时间复杂度为O(m+n))

- 带尾指针(时间复杂度为O(1))

- 带头指针(时间复杂度为O(m+n))
- 双向链表
- 带头结点的双向链表

- 带头结点的双向循环链表
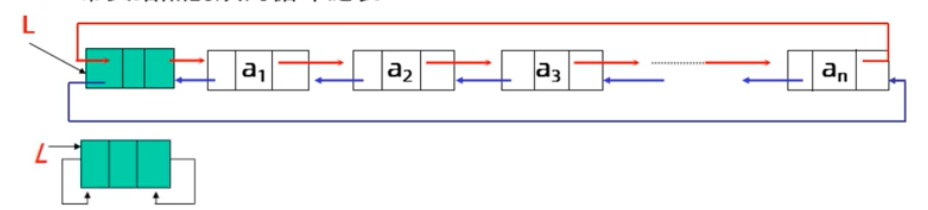
- 双向链表的定义
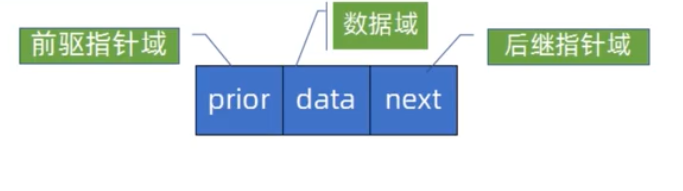
typedef struct DuLNode{ ElemType data; struct DuLNode *prior; struct DuLNode *next; }DuLNode,*DuLinkList;
- 双向链表的插入
1.插在P的前面
Status DuInsertList(DuLinkLIst L,int i,ElemType e){ if(!(s=(DuLinkList)malloc(sizeof(DuLNode)))) return ERROR; DuLinkList s; s->data=e; s->prior=p->prior; p->prior->next=s; s->next=p; p->prior=s; return OK; }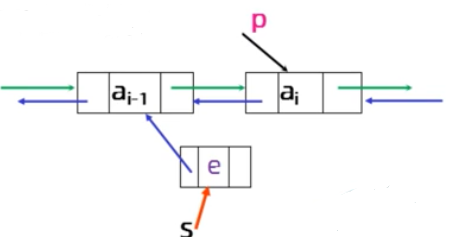
2.插在P的后面
Status DuInsertList(DuLinkLIst L,int i,ElemType e){ //在i中确认插入位置使得指针p指向第i个结点 //若i不合法,则返回ERROR if(!(s=(DuLinkList)malloc(sizeof(DuLNode)))) return ERROR; DuLinkList s; s->data=e; s->next=p->next; p->next->prior=s; s->prior=p; p->next=s; return OK; }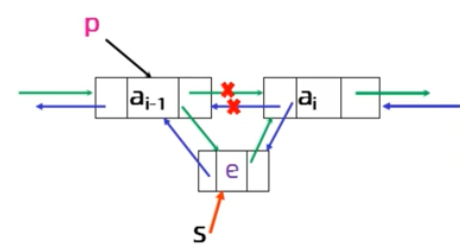
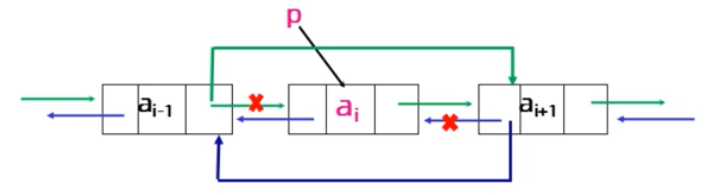
- 双向链表的删除
Status DuInsertList(DuLinkLIst L,int i,ElemType e){ //在i中确认插入位置使得指针p指向第i个结点 //若i不合法,则返回ERROR if(!(s=(DuLinkList)malloc(sizeof(DuLNode)))) return ERROR; DuLinkList s; s->data=e; e=p->data; p->prior->next=p->next; p->next->prior=p->prior; free(p); return OK; }
- 带头结点的双向链表
- 单链表*
- 一元多项式的表示与加减
- 结点结构
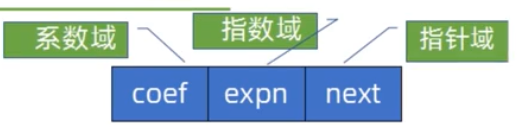
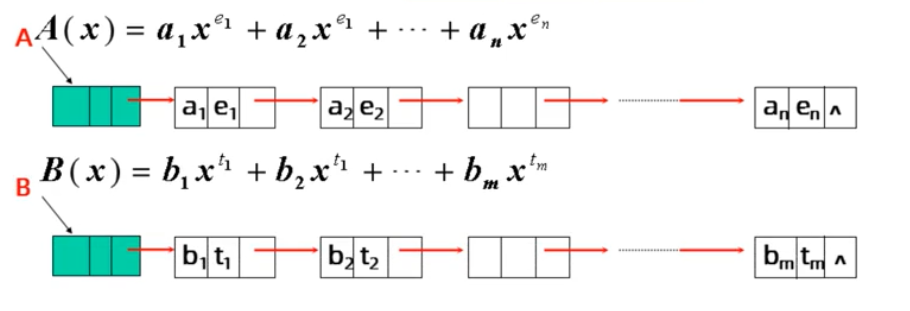
- 结点结构
- 顺序表与链表的比较
具体要求 顺序表 链表 基于空间 表长度变换不大,且易于事先确定其大小
表长度变化大,或难以估计其存储规模时采用
基于时间 随机存取结构
当线性表的操作主要是查找时,宜采用
插入删除频繁的情况
当然若插入删除主要在表的首尾两端,则宜采用尾指针表示的单循环链表。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号