并查集

并查集及其应用

咸鱼说并查集22年加入考研大纲，到目前（25考研之前）还没有考过，可以压一手。

定义

并查集用于解决元素分组的相关问题，也就是对于一组元素，挑出一个来当作代表。
并查集可以视作一种树状的数据结构，每个元素结点都有一个父节点（父节点可以是自己，此时这个结点为代表）。
并查集有 2 种操作：

• 合并（Union）：把两个不相交的元素集合并成一个集合。
• 查询（Find）：查询两个元素是否在同一个集合中。

并查集最重要的特性是，用集合中的一个元素结点代表整个集合。

初始简易版本

初始化

一开始每个元素结点自己一个人一组，此时自己作为自己的父节点。

//初始化
int fa[N];
void init(int n)
{
    for (int i = 1; i <= n; ++i)
        fa[i] = i;
}

合并

合并需要找到两个集合的代表，把一个代表的父亲设为另一个代表，通常把前者的父亲设置为后置。

// 合并
void merge(int x, int y)
{
	int fx = find(x);
	int fy = find(y);
    if(fx == fy)return; // 同一个代表，同一个集合，不用合并
    fa[fx] = fy;
}

查询

用递归的方式，一步步网上找父亲，最后找到的为代表元素（即自己作为自己父亲的）。若两个元素在同一个集合，则它们查询到的代表是同一个。

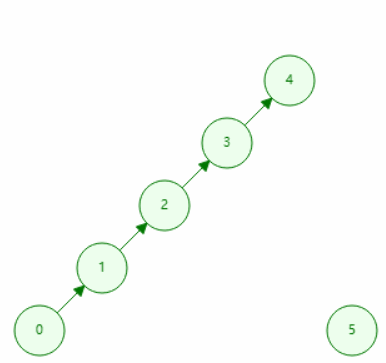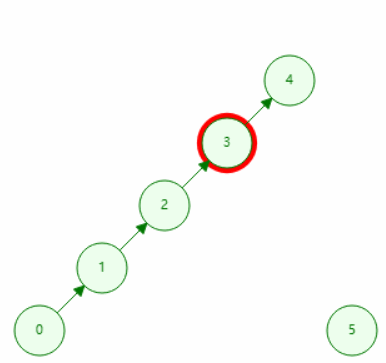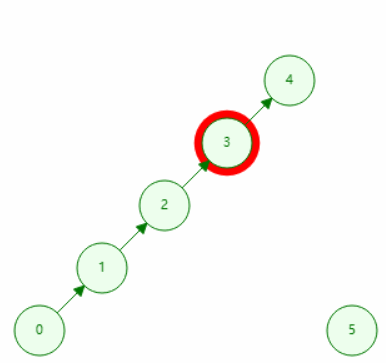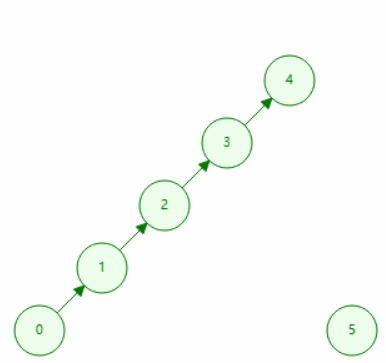
// 查询
int find(int x)
{
    if(x == fa[x])
        return x;
    else{
        return find(fa[x]);
    }
}

简易版本的缺点

很明显，在合并的过程中，并查集可能退化成链表，影响进一步查询和合并的效率，为解决这个问题，有路径压缩和按秩合并两种策略。

路径压缩版本

在查询过程中直接把父亲设置为最终查询到的代表元素（书上的根节点）。
老吕布了。

路径压缩的查询

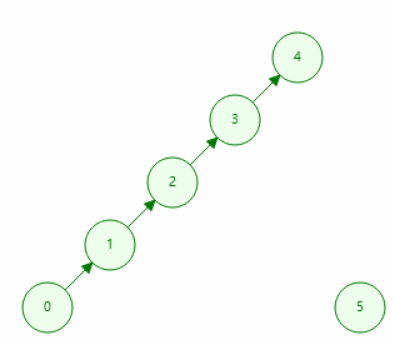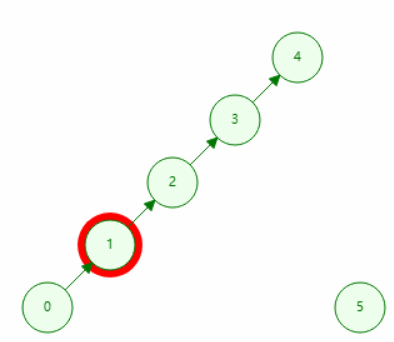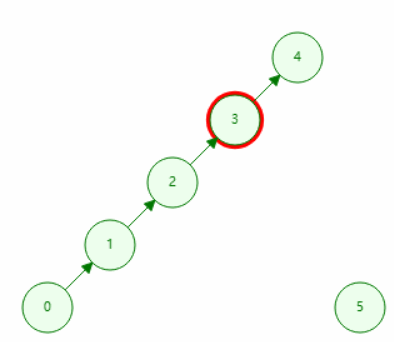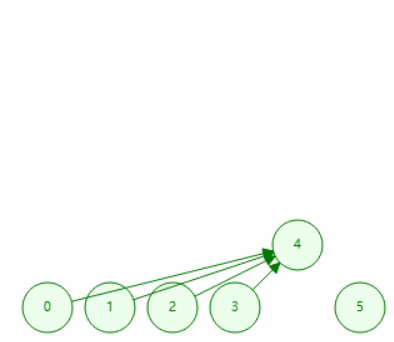
// 查询
int find(int x)
{
    if(x == fa[x])
        return x;
    else{
        return fa[x] = find(fa[x]);  //父节点设为根节点，返回父节点
    }
    // 或者把上述代表写成一行
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}

初始化与合并跟简易版本一样。

按秩合并

这里要给结点赋予秩的属性，这里的秩可以是树的深度，也可以是结点个数，此处以树深为例。

按秩合并初始化

//初始化
int fa[N];
int rank[N];
void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = i;
        rank[i] = 1; // 一开始一个一组，深度为1
    }
}

按秩合并

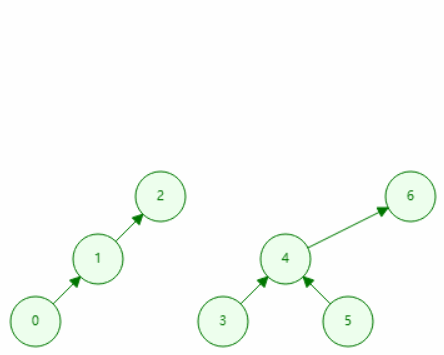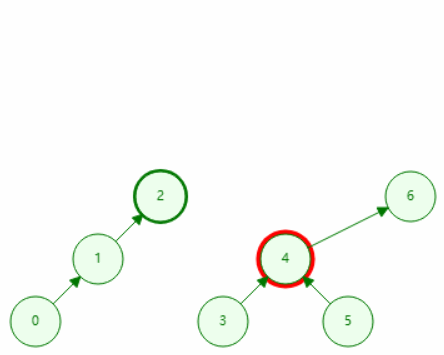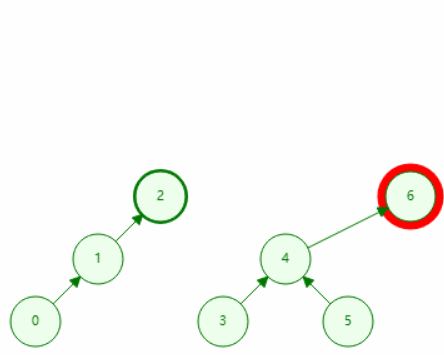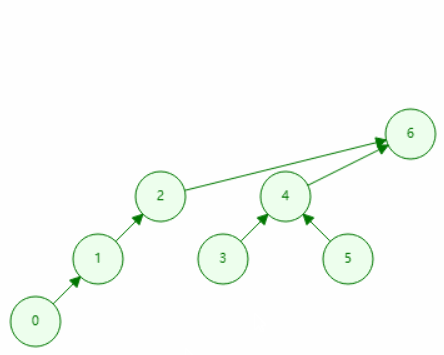
void merge(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(rank[fx] <= rank[fy]){
        fa[fx] = fy;
    }else{
        fa[fy] = fx;
    }
    if(rank[fx] == rank[fy] && fx != fy) // 两棵深度一样的树合并之后的新树深度+1
}

参考文章

算法学习笔记(1) : 并查集 - 知乎 (zhihu.com)
并查集 - OI Wiki (oi-wiki.org)
并查集可视化