OO第一单元总结

第一单元的作业是对表达式进行求导，一共有三次作业。作业要求的不同点在于：

第一次作业表达式中只有幂函数和有符号整数。

第二次作业增加了三角函数，但不能嵌套。

第三次作业三角函数内可以嵌套其他因子。

三次作业从关系上来看是一脉相承、由简入繁，但由于我是第一次使用面向对象语言的缘故，我三次作业的代码并不是依次累加，而是每一次都几乎重写了代码，以下是我对三次作业以及从作业中学习到的东西的总结。

 

第一次作业

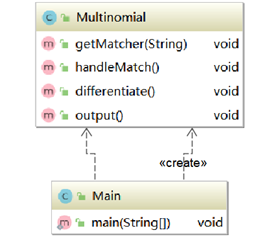
在做第一次作业时，我的思想还处在面向过程语言的桎梏当中，因此我只是简单分成了两个类：一个类提供方法，一个类调用方法。程序结构的分析如下图：

类图：

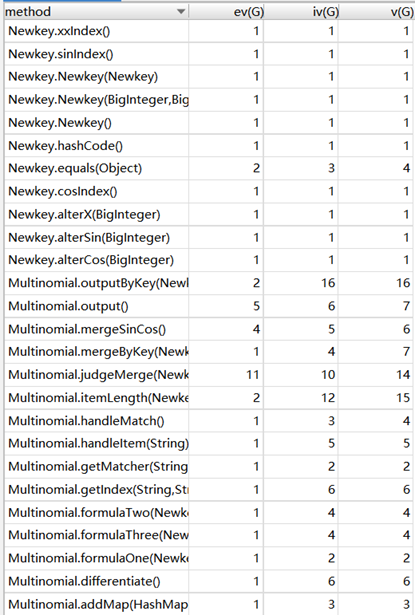
复杂度分析：

 

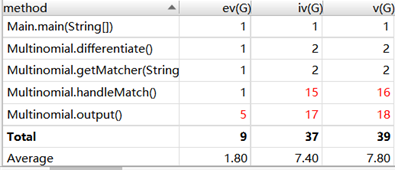
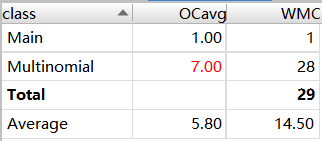
在这一次作业当中，我学到的最重要的知识就是正则表达式的使用。通过正则表达式，可以轻易的把表达式分为项，然后通过正则表达式找到每一项的特征：系数和指数，就可以求出导数，合并也只需把指数相同的项系数相运算就可以了。

第一次作业中没有出现bug。

 

第二次作业

第二次作业相较于第一次作业并没有发生质的变化。由于加入了sin(x)和cos(x)，每一项的特征变为了：系数、x的指数、sin(x)的指数、cos(x)的指数，所以我改用hashmap存储项，并新建一个类作为hashmap的key保存了三个指数。同样用正则表达式把表达式分割成项，然后计算项的系数和各个指数，再进行合并。

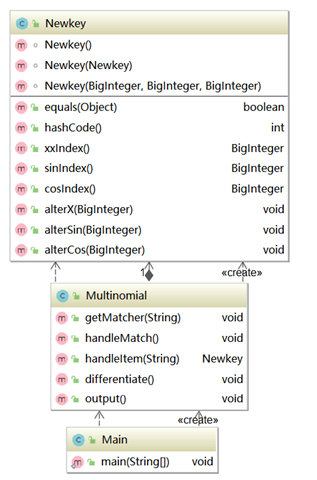
这一次的作业的代码当中也没有体现出面向对象语言的特点，程序结构分析如下图：

类图：

复杂度分析：

第二次作业合并同类项不能像第一次一样只合并指数相同的项，而是可以利用公式：sin(x)^2 + cos(x)^2 = 1，sin(x)^2 = 1 – cos(x)^2和cos(x)^2 = 1 – sin(x)^2进行更多的合并。我在合并当中出现了一个bug，由于条件写错了，在不该使用公式合并项的时候错误地合并了项。

 

第三次作业

第三次相比于前两次作业复杂了许多。由于允许嵌套，所以在处理表达式时不能用之前的线性处理方式，而是要递归地依次处理嵌套的各层，这样使得我的代码更加结构化，对象在代码中的重要性也凸显出来。

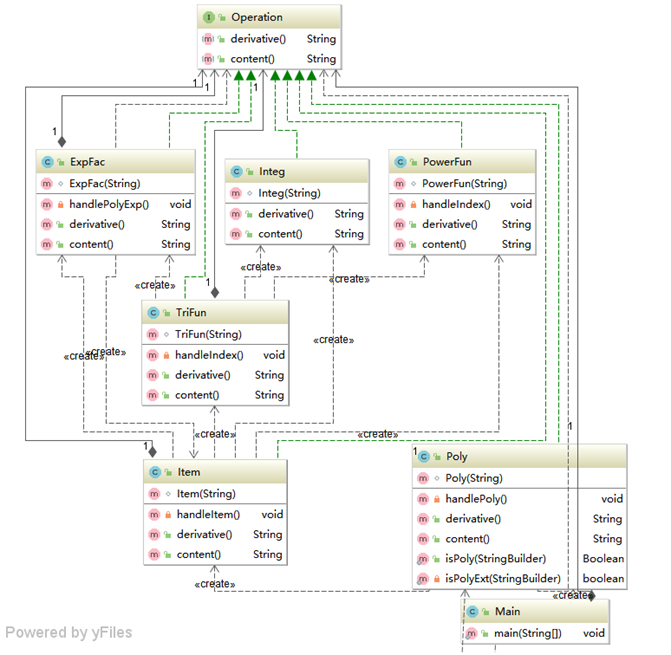
依照老师的提示，对不同因子以及不同的因子间运算方式建立了不同的类，这些类需要共同实现的方法，求导和返回保存的内容。因此建立了一个接口，包含了这两个方法，让各个类实现这个接口。然后便是类似于编译原理中的语法分析一样，在当前对象的求导方法中调用当前对象产生的对象的求导方法，以此实现嵌套函数的求导。程序结构的分析如下图：

类图：

复杂度分析：

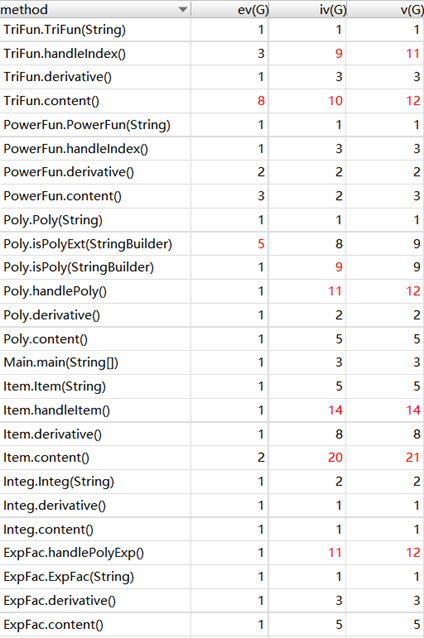
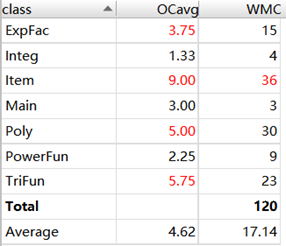
由于第三次代码做了一些形式上比较复杂的优化，加之我的求导和优化是分开做的（也就是说，我进行了两次递归地生成对象再返回的过程），导致了运行时间较长，因此在强测中有两个点超出了允许的运行时间。除此之外，没有什么bug。

 

三次作业的对比

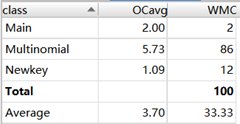
第一次作业有两个类，第二次作业有三个类，第三次作业有八个类

把第二次作业和第三次作业进行比较，第二次作业最长的类写了454行，其中包含了许多重复的代码，而第三次作业最长的类只有158行。虽然两次作业不同，第三次作业的总代码数超过了第二次作业，但第三作业还是更简洁、更具结构。每个类包含较少的内容使得debug的过程中能够更快的找到错误所在的地方，减少耦合度也能增加程序的可维护性。

 

测试程序的方法

我没有参与互测，因此我谈一谈我测试自己代码的方法。

对于正确样例，要做到可能类型的全覆盖。输入时，要考虑到所有可能类型的输入，比如有无系数，有无某种因子，因子有无指数，嵌套内部是哪种因子，嵌套的层次有几层（这个无法无限深层，所以我在测试中一般表达式最多包含四层，然后单独测试嵌套许多层的表达式），有符号整数的正负，正数前面是否有加号等情况，组合起来进行测试；对于输出，我单独把输出部分的代码拿出来进行测试以便检查是否按构想的输出，主要测试省略指数、系数，合并同类项，去括号的情况，尤为要注意的测试不该省略的时候不能误省略。

对于错误样例，题目要求中已经说明白了判断为错误样例的情况。前两次作业写好正则表达式，第三次作业正则表达式加上指数的限制就可以完成对错误样例的判断。测试中就是测试可能出现的不满足正则表达式和超出指数限制的情况。

 

创建模式

第三次作业在处理输入表达式时，我是在构造函数中判断当前对象需要生成哪些新的对象，这样导致了每一个类的构造函数里都有许多条件语句。在阅读讨论区中大家的讨论后，我发现工厂模式非常适合我写的代码，可以将各个类的构造函数的一部分相同的内容放入到一个工厂内，更利于代码的维护。