网络流1

 -A.板子

从“课本”上贺的。

code

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

const int maxn = 1e3 + 2;
const int maxm = 1e5 + 3;
const int inf = 1 << 29;
//const int mod = 1e9 + 7;

int n, m, s, t, tot, maxflow;
int d[maxn], now[maxn];
queue<int> q;

struct node 
{
    int to, nxt, w;
}a[maxm<<1];
int len, head[maxn];

void add(int x, int y, int w)
{
    a[++len].to = y; a[len].w = w; a[len].nxt = head[x]; head[x] = len;
    a[++len].to = x; a[len].w = 0; a[len].nxt = head[x]; head[x] = len;
}

bool bfs()
{
    memset(d, 0, sizeof(d));
    while(q.size()) q.pop();
    q.push(s); d[s] = 1; now[s] = head[s];
    while(q.size())
    {
        int x = q.front(); q.pop();
        for(int i=head[x]; i; i=a[i].nxt)
        {
            if(a[i].w && !d[a[i].to])
            {
                q.push(a[i].to);
                now[a[i].to] = head[a[i].to];
                d[a[i].to] = d[x] + 1;
                if(a[i].to == t) return 1;
            }
        }
    }
    return 0;
}

int dinic(int x, int flow)
{
    if(x == t) return flow;
    int rest = flow, k, i;
    for(i=now[x]; i&&rest; i=a[i].nxt)
    {
        now[x] = i;
        if(a[i].w && d[a[i].to] == d[x]+1)
        {
            k = dinic(a[i].to, min(rest, a[i].w));
            if(!k) d[a[i].to] = 0;
            a[i].w -= k;
            a[i^1].w += k;
            rest -= k;
        }
    }
    return flow - rest;
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    len = 1;
    for(int i=1; i<=m; i++)
    {
        int u, v, c; scanf("%d%d%d", &u, &v, &c);
        add(u, v, c);
    }
    int flow = 0;
    while(bfs())
        while(flow = dinic(s, inf)) maxflow += flow;
    printf("%d", maxflow);

    return 0;
}

 

A. 蜥蜴

我坚信我背的板子是对的，结果我记错了，k = dinic(y, min(rest, a[i].w)被我记成了和flow取min……

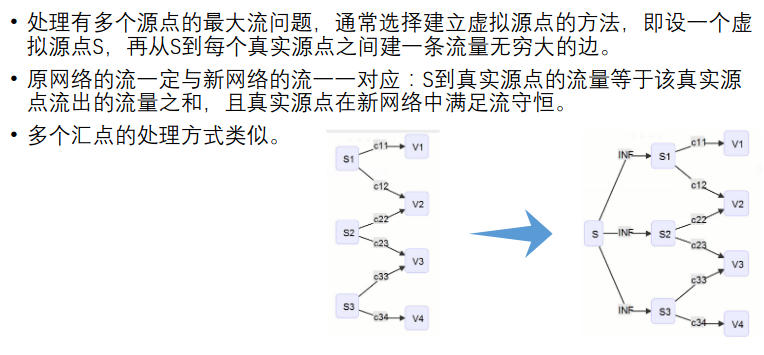
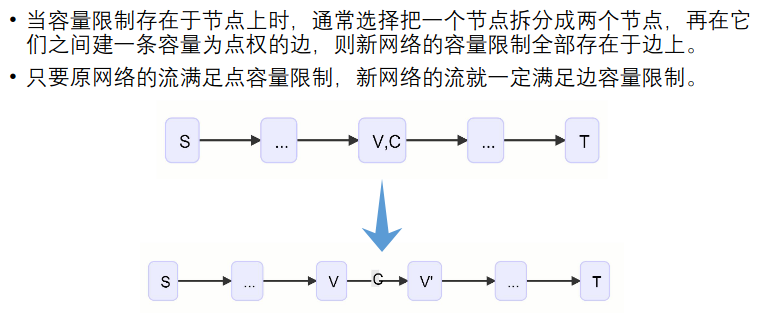
对建反向边理解还不深刻，有的边反向了有的边没反向，还把源点到蜥蜴全都连成了inf，事实上应该连1，因为最大流答案不能超过蜥蜴总数，有蜥蜴的石柱上只有一只，没有更多的能逃出去。

网络流的第一个题，充分表现出Cat啥都没学会***

 

#include <bits/stdc++.h>
  
using namespace std;
  
typedef long long ll;
const int maxn = 100019;
const int N = 505;
const ll mod = 1e9 + 7;
const int inf = (1<<29);

int num, D, lenx, leny, mp[190][190], maxflow, L[190][190];
queue<int> q;
char s1[maxn];
int s, t, tot, d[maxn];

struct node2
{
    int x, y, dis;
}c1[N];

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

double getdis(int x1, int y1, int x2, int y2)
{
    return ((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}

int getindex(int x, int y)
{
    return (x-1)*leny + y;
}

struct node 
{
    int next, to, w;
}a[maxn<<2];
int head[maxn], len=1, now[maxn];

void add(int x, int y, int w)
{
    a[++len].to = y; a[len].next = head[x]; a[len].w = w;
    head[x] = len;
}

bool bfs()
{
    memset(d, 0, sizeof(d));
    while(q.size()) q.pop();
    q.push(s); d[s] = 1; now[s] = head[s];
    while(q.size())
    {
        int x = q.front(); q.pop();
        for(int i=head[x]; i; i=a[i].next)
        {
            int y = a[i].to;
            if(a[i].w && !d[y])
            {
                q.push(y);
                now[y] = head[y];
                d[y] = d[x] + 1;
                if(y == t) return 1;
            }
        }
    }
    return 0;
}

int dinic(int x, int flow)
{
    if(x == t) return flow;
    int rest = flow, k, i;
    for(i=now[x]; i && rest; i=a[i].next)
    {
        now[x] = i;
        int y = a[i].to;
        if(a[i].w && d[y] == d[x] + 1)
        {
            k = dinic(y, min(rest, a[i].w));
            if(!k) d[y] = 0;
            a[i].w -= k;
            a[i^1].w += k;
            rest -= k;
        }
    }
    return flow - rest;
}

int main()
{
    lenx = read(); leny = read(); D = read();
    for(int i=1; i<=lenx; i++)
    {
        scanf("%s", s1+1);
        for(int j=1; j<=leny; j++)
        {
            mp[i][j] = s1[j]-'0';
        }
    }
    for(int i=1; i<=lenx; i++)
    {
        scanf("%s", s1+1);
        for(int j=1; j<=leny; j++)
        {
            if(s1[j] == 'L')
            {
                L[i][j] = 1;
                num++;
            }
        }
    }
    tot = lenx * leny;
    s = tot * 2 + 1; t = s + 1;
    for(int i=1; i<=lenx; i++)
    {
        for(int j=1; j<=leny; j++)
        {
            int I = getindex(i, j);
            if(mp[i][j])
            {
                add(I, I+tot, mp[i][j]);
                add(I+tot, I, 0);
                if(i+D>lenx || i-D<1 || j+D>leny || j-D<1)
                {
                    add(I+tot, t, inf);
                    add(t, I+tot, inf);//反向也有边权是因为t既是入点又是出点
                }
            }
            if(L[i][j])
            {
                add(s, I, 1);//最大流答案不能超过蜥蜴总数
                add(I, s, 0);
            }
        }
    }
    for(int x1=1; x1<=lenx; x1++)
    {
        for(int y1=1; y1<=leny; y1++)
        {
            for(int x2=1; x2<=lenx; x2++)
            {
                for(int y2=1; y2<=leny; y2++)
                {
                    if(getdis(x1, y1, x2, y2) <= D * D)
                    {
                        int u = getindex(x1, y1), v = getindex(x2, y2);
                        add(u+tot, v, inf);//出点连入点
                        add(v, u+tot, 0);
                        add(v+tot, u, inf);
                        add(u, v+tot, 0);
                    }
                }
            }
        }
    }
    int flow = 0;
    while(bfs())
    {
        while(flow = dinic(s, inf)) maxflow += flow;
    }
    printf("%d\n", num - maxflow);
  
    return 0;
}

 

B. 星际战争

既然放在了最大流的分区，那就联想一下和最大流的关系，要不是因为专题我绝对联想不到最大流：

思路1.把n和m都拆成两个点，两个点中间的边权就是装甲值或攻击强度，然后求出来的最大流就是单位时间的有效进攻量，再用总数除以这个最大流。然后忽然发现这样被攻击的点有的满了有的没满，所以用总数直接除是错的……

思路2.n还是一个点，把m拆了，源点到n和n到m的入点都是inf，然后算出最大流的情况下1~n每个点流出的流量，再分别除以B[i]，emmm似乎有一点点道理的样子……

不过以上都不是正解，正解是二分答案，每一次二分重新建图，激光武器的边权改成t*B[i]，判断总流量能否达到A[i]的和。而且，这道题居然并不需要拆点。

鹤一篇题解？？算了改天再鹤……

 

 

upd：

关于会记错板子这件事，我认为是没学会，所以打算重学。

打算从EK开始。

code

//叩首问路，码梦为生
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 1e5 + 3;

void add(int x, int y, int z)
{

}

bool bfs()
{
    memset(v, 0, sizeof(v));
    queue<int> q;
    q.push(s); v[s] = 1;
    incf[s] = inf;
    while(q.size())
    {
        int x = q.front(); q.pop();
        for(int i=head[x]; i; i=a[i].nxt)
        {
            if(a[i].w)
            {
                int y = a[i].to;
                if(v[y]) continue;
                incf[y] = min(incf[x], a[i].w);
                pre[y] = i;
                q.push(y), v[y] = 1;
                if(y == t) return 1;
            }
        }
    }
    return 0;
}

void update()
{
    int x = t;
    while(x != s)
    {
        int i = pre[x];
        a[i].w -= incf[t];
        a[i^1].w += incf[t];
        x = a[i^1].to;
    }
    maxflow += incf[t];
}

int main()
{
    while(cin >> m >> n)
    {
        memset(jead, 0, sizeof(head));
        s = 1, t = n; tot = 1; maxflow = 0;
        for(int i=1; i<=m; i++)
        {
            int x, y, c; scanf("%d%d%d", &x, &y, &c);
            add(x, y, c);
        }
        while(bfs()) update();
        cout << maxflow << endl;
    }

    return 0;
}