来自学长的告别

B. Star Way To Heaven

我写了一个二分，但是惊奇的发现check(1.1180339887)是对的，而最后输出的答案确是1.11803187...巨大的精度误差啊，（手动二分答案都出来了）

调错解的结果就是在写正解之前就知道让它输出%.10Lf的答案是1.1180339887

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 6007;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;

long double n, m, l, r, b[maxn];
int k, tot;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct node 
{
    long double x, y;
    int fa;
    bool operator < (const node &T) const 
    {
        return fa < T.fa;
    }
}p[maxn];

bool Near(int i, int j, double len)
{
    long double rod = (p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y);
    long double rol = len*2.0;
    //printf("main cmp : %.3lf %.3lf\n", rod, rol*rol);
    if(rod > rol*rol) return 0;
    else return 1;
}

int find(int x)
{
    if(x == p[x].fa) return x;
    return p[x].fa = find(p[x].fa);
}

struct node2 
{
    int l, r, sum, lazy;
}tree[maxn<<2];

#define lson (rt<<1)
#define rson (rt<<1|1)

void build(int rt, int l, int r)
{
    tree[rt].l = l; tree[rt].r = r;
    if(l == r)
    {
        tree[rt].sum = 0;
        return;
    }
    int mid = (l + r) >> 1;
    build(lson, l, mid);
    build(rson, mid+1, r);
}

void pushup(int rt)
{
    tree[rt].sum = tree[lson].sum + tree[rson].sum;
}

void pushdown(int rt)
{
    if(tree[rt].lazy)
    {
        int lz = tree[rt].lazy;
        tree[rt].lazy = 0;
        tree[lson].lazy = lz;
        tree[rson].lazy = lz;
        tree[lson].sum = lz*(tree[lson].r-tree[lson].l+1);
        tree[rson].sum = lz*(tree[rson].r-tree[rson].l+1);
    }
}

void update(int rt, int l, int r, int ff)
{
    if(l <= tree[rt].l && tree[rt].r <= r)
    {
        tree[rt].sum = ff*(tree[rt].r-tree[rt].l+1);
        tree[rt].lazy = ff;
        return;
    }
    pushdown(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if(l <= mid) update(lson, l, r, ff);
    if(r > mid) update(rson, l, r, ff);
    pushup(rt);
}

bool check(double len)
{
    for(int i=1; i<=k; i++)
    {
        p[i].fa = i;
    }
    memset(b, 0, sizeof(b)); tot = 0;
    b[++tot] = len;
    //printf("b[%d] = %.2lf\n", tot, b[tot]);
    for(int i=1; i<=k; i++)
    {
        b[++tot] = p[i].y - len; 
        if(b[tot] < 0) b[tot] = len; if(b[tot] > m-len) b[tot] = m-len;
        //printf("b[%d] = %.2lf\n", tot, b[tot]);
        b[++tot] = p[i].y + len;
        if(b[tot] < 0) b[tot] = len; if(b[tot] > m-len) b[tot] = m-len;
        //printf("b[%d] = %.2lf\n", tot, b[tot]);
    }
    b[++tot] = m - len;
    //printf("b[%d] = %.2lf\n", tot, b[tot]);
    sort(b+1, b+1+tot);
    //if(b[1] < 0) return 0;
    /*for(int i=1; i<=tot; i++)
    {
        printf("b[%d] = %.2lf\n", i, b[i]);
    }*/
    int num = unique(b+1, b+1+tot) - b - 1;
    /*for(int i=1; i<=num; i++)
    {
        printf("b[%d] = %.2lf\n", i, b[i]);
    }*/
    build(1, 1, num);
    for(int i=2; i<=k; i++)
    {
        for(int j=1; j<i; j++)
        {
            if(Near(i, j, len))
            {
                int fx = find(j), fy = find(i);
                p[fx].fa = fy;
            }
        }
    }
    /*for(int i=1; i<=k; i++)
    {
        printf("p[%d].fa = %d\n", i, p[i].fa);
    }*/
    sort(p+1, p+1+k);
    int x = 0, y = 0;
    //int x = lower_bound(b+1, b+1+num, len) - b;
    //int y = lower_bound(b+1, b+1+num, m-len) - b;
    //update(1, 1, x, 1); update(1, y+1, num, 1);
    //printf("add(1, %d)\n", x);
    //printf("add(%d, %d)\n", y+1, num);
    //add(1, x); add(y+1, num);
    //add 1
    x = lower_bound(b+1, b+1+num, p[1].y-len) - b;
    y = lower_bound(b+1, b+1+num, p[1].y+len) - b;
    update(1, x, y, 1);
    //printf("add(%d, %d)\n", x, y);
    //add(x, y);
    for(int i=2; i<=k; i++)
    {
        if(p[i].fa == p[i-1].fa)
        {
            x = lower_bound(b+1, b+1+num, p[i].y-len) - b;
            y = lower_bound(b+1, b+1+num, p[i].y+len) - b;
            update(1, x, y, 1);
            //add(x, y);//add i
        }
        else 
        {
            //printf("ccccc %d %d\n", tree[1].sum, num);
            if(tree[1].sum == num) return 0;
            //if(query(num) == num) return 0;
            //memset(c, 0, sizeof(c));
            update(1, 1, num, 0);
            //update(1, 1, x, 1); update(1, y+1, num, 1);
        }
    }
    //printf("ccccc %d %d\n", tree[1].sum, num);
    if(tree[1].sum == num) return 0;
    return 1;
}

int main()
{
    scanf("%Lf%Lf", &n, &m); k = read();
    for(int i=1; i<=k; i++)
    {
        p[i].x = read(); p[i].y = read();
    }
    //sort(p+1, p+1+k);
    //tiao check
    //bool ggg = check(1.1180339887);
    //printf("ggg = %d\n", ggg);

    l = 0, r = m;
    while(r-l > 1e-13)
    {
        //printf("%.7Lf %.7Lf\n", l, r);
        long double mid = (l+r+0.102959999999)/2.0;
        //printf("mid = %.7Lf\n", mid);
        if(check(mid)) l = mid;
        else r = mid - 0.000000000001;
    }
    printf("%.8Lf", l);
    
    return 0;
}

 正解：从下界到上界连边，部分分是二分完了判断连通性，会T，另一种方法是最小生成树，在一棵生成树上每两个点之间都是连通的，最小是因为能为卡死道路贡献最大的一定是间距最小的使得上下边界连通的路径，以len为半径画的圆覆盖这些路径是连通的最低要求，答案就是不能让连通的要求被满足，那就是破坏掉其中最容易被破坏的条件——最小生成树上最长的边，它的两端是两条半径，所以ans/=2.

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 6007;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;

long double n, m, ans, X[maxn], Y[maxn], dis[maxn];
bool vis[maxn];
int k;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

long double cal(long double i1, long double j1, long double i2, long double j2)
{
    return sqrt((i1-i2)*(i1-i2)+(j1-j2)*(j1-j2));
}

int main()
{
    scanf("%Lf%Lf", &n, &m); k = read();
    for(int i=1; i<=k; i++)
    {
        scanf("%Lf%Lf", &X[i], &Y[i]);
        dis[i] = Y[i];
    }
    dis[k+1] = m;
    while(1)
    {
        ll mi = 0;
        for(int j=1; j<=k+1; j++)
        {
            if(!vis[j] && (mi==0||dis[j]<dis[mi]))
            {
                mi = j;
            }
        }
        ans = max(ans, dis[mi]);
        vis[mi] = 1;
        if(mi == k+1)
        {
            printf("%.10Lf\n", ans/2);
            exit(0);
        }
        for(int j=1; j<=k; j++)
        {
            dis[j] = min(dis[j], cal(X[j], Y[j], X[mi], Y[mi]));
        }
        dis[k+1] = min(dis[k+1], (long double)(m-Y[mi]));
    }
    
    return 0;
}

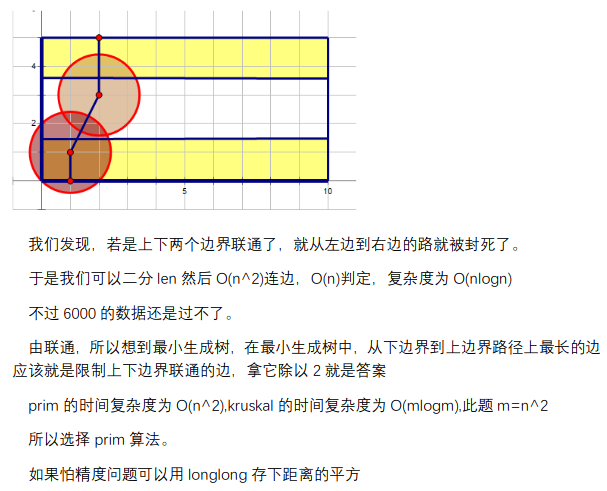
 二分的话，按y排序可能有必要？因为排不排序都需要n^2连边……

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 6007;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;
const double eps = 1e-6;

int n, m, k, fa[maxn], poi[maxn];
double l, r, dis[maxn];

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct node 
{
    double x, y;
}p[maxn];

bool cmp(const int a, const int b)
{
    return dis[a] < dis[b];
}

int find(int x)
{
    if(x == fa[x]) return x;
    return fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
    int fx = find(x), fy = find(y);
    fa[fx] = fy;
}

double get_dis(int i, int j)
{
    return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}

bool check(double len)
{
    for(int i=1; i<=k+2; i++)
    {
        fa[i] = i;
    }
    for(int i=1; i<=k; i++)
    {
        if(m-p[i].y<=2*len) merge(i, k+1);
        if(p[i].y<=2*len) merge(i, k+2);
        if(find(k+1) == find(k+2)) return 0;
    }
    for(int i=1; i<=k; i++)
    {
        for(int j=i+1; j<=k; j++)
        {
            if(get_dis(poi[i], poi[j])<=2*len)
            {
                merge(poi[i], poi[j]);
                if(find(k+1) == find(k+2)) return 0;
            }
        }
    }
    return 1;
}

int main()
{
    n = read(); m = read(); k = read();
    for(int i=1; i<=k; i++)
    {
        int x = read(), y = read();
        p[i] = (node){(double)x, (double)y};
        dis[i] = get_dis(i, 0);
        poi[i] = i;
    }
    sort(poi+1, poi+k+1, cmp);
    l = 0, r = m / 2.0;
    while(r-l > eps)
    {
        double mid = (l+r)/2.0;
        if(check(mid)) l = mid;
        else r = mid;
    }
    printf("%.9lf\n", l);
    
    return 0;
}

 事实证明，排序就是很多余***不过不管是什么版本的二分都没有像我那么傻呵呵地用线段树+伪扫描线的思路来判断连通性***至于我也用到了并查集，那是为了更新方便一起操作不记录次数，没派上正经的用场……

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 6007;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;
const double eps = 1e-6;

int n, m, k, fa[maxn];
double l, r, dis[maxn];

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

struct node 
{
    double x, y;
}p[maxn];

int find(int x)
{
    if(x == fa[x]) return x;
    return fa[x] = find(fa[x]);
}

void merge(int x, int y)
{
    int fx = find(x), fy = find(y);
    fa[fx] = fy;
}

double get_dis(int i, int j)
{
    return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
}

bool check(double len)
{
    for(int i=1; i<=k+2; i++)
    {
        fa[i] = i;
    }
    for(int i=1; i<=k; i++)
    {
        if(m-p[i].y<=2*len) merge(i, k+1);
        if(p[i].y<=2*len) merge(i, k+2);
        if(find(k+1) == find(k+2)) return 0;
    }
    for(int i=1; i<=k; i++)
    {
        for(int j=i+1; j<=k; j++)
        {
            if(get_dis(i, j)<=2*len)
            {
                merge(i, j);
                if(find(k+1) == find(k+2)) return 0;
            }
        }
    }
    return 1;
}

int main()
{
    n = read(); m = read(); k = read();
    for(int i=1; i<=k; i++)
    {
        int x = read(), y = read();
        p[i] = (node){(double)x, (double)y};
    }
    l = 0, r = m / 2.0;
    while(r-l > eps)
    {
        double mid = (l+r)/2.0;
        if(check(mid)) l = mid;
        else r = mid;
    }
    printf("%.9lf\n", l);
    
    return 0;
}

 

C. God Knows

问题被转化成了极长上升子序列，因为那些不属于这个序列的一定会被消掉，f[i]表示以i为结尾的极长上升子序列的代价的最小值。暴力也有一些小细节：它必须是极长的，因此倒序循环记录mx，比mx小的不能转移，f[i]是以i结尾的，放到整个序列中极长的含义就消失了，不能取maxf更不能直接用f[n]，所以添加一个一定能转移的f[n+1]。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 2e5 + 3;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;

int n, c[maxn], p[maxn];
ll f[maxn];

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

int main()
{
    n = read();
    for(int i=1; i<=n; i++)
    {
        p[i] = read();
    }
    for(int i=1; i<=n; i++)
    {
        c[i] = read();
    }
    p[n+1] = n+1;
    for(int i=1; i<=n+1; i++)
    {
        int mx = 0;
        f[i] = INF;
        for(int k=i-1; k>=0; k--)
        {
            if(p[k] < mx) continue;
            if(p[k] < p[i])
            {
                f[i] = min(f[i], f[k]+c[i]);
                mx = max(mx, p[k]);
            }
        }
    }
    printf("%lld\n", f[n+1]);
    
    return 0;
}

 不过是一些对题解的解释，我搜到的题解有点抽象……

val[]是记录叶子节点的最优解，vl[]是记录从下向上传递，当前节点左子树中的最优解，mx[]记录最晚出现的时间(i，也就是p的下标)，id是最优解已转移的最优解中的最大时间(mx)，v是最优解的值，线段树位置对应p。

query是通过查询[1, p[i[-1]给id和v赋值，为什么参数只有p[i]，因为每次左边界都从1开始，省略掉了，又因为查询在更新之前所以查[1, p[i]]和查[1, p[i]-1]是一样的，但事实上把查询p[i]改成p[i]-1会TLE0分，这个问题有待解决……calc是用来找到在当前子树控制的区间范围内最优解的神奇函数。

calc为什么能快速地查到最优解？重点在于线段树pushup时的预处理，所有预处理过的都可以直接赋值，在暴力循环中，按照下标从大到小的顺序枚举，跳过p的值被后来者覆盖的情况，这样计入答案的序列中，随着i减小，p在不断增大，现在把下标和p值交换位置，查找的方法也有了变化——首先，无论i是多少，在之前的时间中（时间通过循环的顺序保证）最大的p一定不会被覆盖，所以向上合并时假设右子树已经走过，只要时间比已经找到的最优解里面的最大值（右子树上记录的）更早，那都要“删掉”，因为线段树是按照p建的，左子树p一定更小，更小且更晚就不合法，所以在向上pushup时传入的参数是mx[rson]。至于查询，因为第一个转移点相当于还没找到，不能设限，而找到第一个转移点之后就需要设限了，因为线段树预处理区间的不连续性，这是id的用途。

因为线段树上大区间被分成了一个个的小区间，查到的最优解仅代表当前范围内的，所以还要在整个p更小的范围内取min，因为v要取min，必须要赋值INF，但是如果在区间范围内找不到满足条件的任何最优解它的INF就没有变化，在实际意义上这个数就是作为第一个数出现了，前面应该是0，再改成0。

有的题解说这道题要用到李超线段树，但我理解的这篇题解好像只是普通的线段树而已。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 2e5 + 3;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;

int n, p[maxn], c[maxn], mx[maxn<<2], val[maxn<<2], vl[maxn<<2];

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}

int calc(int i, int l, int r, int d)
{
    //printf("i = %d l = %d r = %d d = %d\n", i, l, r, d);
    if(l == r) return mx[i]>d?val[i]:INF;
    int mid = (l + r) >> 1;
    if(mx[i<<1|1]<=d) return calc(i<<1, l, mid, d);
    else return min(vl[i], calc(i<<1|1, mid+1, r, d));
}

void insert(int i, int l, int r, int p, int id, int v)
{
    //printf("i = %d l = %d r = %d p = %d id = %d v = %d\n", i, l, r, p, id, v);
    if(l == r) 
    {
        //printf("mx[%d] = %d\n", i, id);
        //printf("val[%d] = %d\n", i, v);
        mx[i] = id; val[i] = v; return;
    }
    int mid = (l + r) >> 1;
    if(p <= mid) insert(i<<1, l, mid, p, id, v);
    else insert(i<<1|1, mid+1, r, p, id, v);
    mx[i] = max(mx[i<<1], mx[i<<1|1]);
    //printf("mx[%d] = %d\n", i, mx[i]);
    vl[i] = calc(i<<1, l, mid, mx[i<<1|1]);
    //printf("calc(%d, %d, %d, %d)\n", i<<1, l, mid, mx[i<<1|1]);
    //printf("vl[%d] = %d\n", i, vl[i]);
}

int id, v;
void query(int i, int l, int r, int p)
{
    //printf("i = %d l = %d r = %d p = %d\n", i, l, r, p);
    if(r <= p)
    {
        //printf("v = %d id = %d\n", v, id);
        //printf("mx[%d] = %d\n", i, mx[i]);
        v = min(v, calc(i, l, r, id)), id = max(id, mx[i]); 
        //printf("-----v = %d id = %d\n", v, id);
        //printf("-----mx[%d] = %d\n", i, mx[i]);
        return;
    }
    int mid = (l + r) >> 1;
    if(mid < p) query(i<<1|1, mid+1, r, p);
    query(i<<1, l, mid, p);
}

int main()
{
    n = read();
    for(int i=1; i<=n; i++)
    {
        p[i] = read();
    }
    for(int i=1; i<=n; i++)
    {
        c[i] = read();
    }
    for(int i=1; i<=n*4; i++)
    {
        vl[i] = INF;
    }
    for(int i=1; i<=n; i++)
    {
        id = 0, v = INF;
        query(1, 1, n, p[i]);
        //printf("query(1, 1, %d, %d)\n", n, p[i]);
        insert(1, 1, n, p[i], i, (v<INF?v:0)+c[i]);
        //printf("insert(1, 1, %d, %d, %d, %d)\n", n, p[i], i, (v<INF?v:0)+c[i]);
    }
    id = 0, v = INF; query(1, 1, n, n);
    //printf("query(1, 1, %d, %d)\n", n, n);
    printf("%d\n", v);
    
    return 0;
}

安利一个看懂题解的好办法，在保证抄对的前提下，输出中间过程，大模拟……

 

D. Lost My Music

%%%学长的题解写得太好了

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 5e5 + 3;
const ll mod = 1e9 + 7;
const int INF = 2147483647;
const int lim = 1e4 + 1;

int n, fa[maxn], c[maxn], dep[maxn], f[maxn][19];
long double ans[maxn];

struct node 
{
    int next, to;
}a[maxn];
int head[maxn], len;

void add(int x, int y)
{
    a[++len].to = y; a[len].next = head[x];
    head[x] = len;
}

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
        {
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = (x << 1) + (x << 3) + (ch^48);
        ch = getchar();
    }
    return x * f;
}
//如果不合法需要弹栈，返回1
bool check(int k, int j, int i)
{
    return 1ll*(c[i]-c[k])*(dep[i]-dep[j])>=1ll*(c[i]-c[j])*(dep[i]-dep[k]);
}

void dfs(int u)
{
    dep[u] = dep[fa[u]] + 1;
    int x = fa[u], t;
    for(int i=18; i>=0; i--)
    {
        if((t=f[x][i])<2) continue;
        if(check(f[t][0], t, u)) x = t;
    }
    if(x!=1 && check(f[x][0], x, u)) x = f[x][0];
    f[u][0] = x;
    for(int i=1; i<=18; i++) 
    {
        f[u][i] = f[f[u][i-1]][i-1];
    }
    for(int i=head[u]; i; i=a[i].next) dfs(a[i].to);
}

int main()
{
    n = read();
    for(int i=1; i<=n; i++)
    {
        c[i] = read();
    }
    for(int i=2; i<=n; i++)
    {
        fa[i] = read();
        add(fa[i], i);
    }
    dfs(1);
    for(int i=2; i<=n; i++)
    {
        printf("%.10lf\n", (c[f[i][0]]-c[i])*1.0/(dep[i]-dep[f[i][0]]));
    }
    
    return 0;
}

void dfs(int u)
{
    dep[u] = dep[fa[u]] + 1;
    int x = fa[u], t;
    for(int i=18; i>=0; i--)
    {
        if((t=f[x][i])<2) continue;
        if(check(f[t][0], t, u)) x = f[t][0];
    }
    if(x!=1 && check(f[x][0], x, u)) x = f[x][0];
    f[u][0] = x;
    for(int i=1; i<=18; i++) 
    {
        f[u][i] = f[f[u][i-1]][i-1];
    }
    for(int i=head[u]; i; i=a[i].next) dfs(a[i].to);
}

这个函数x = f[t][0]也可以过，其实理解的话似乎是调到f[t][0]才合理……