UVA1073 几何 组合数学

UVA1073 Glenbow Museum

好题。

首先拿出纸笔模拟一下，发现 \(\texttt{OO}\) 是不能成立的。

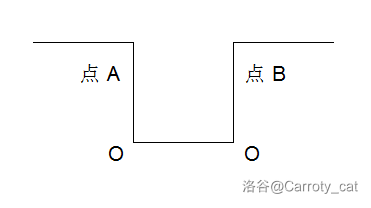
如果有以下这张图：

可以发现，没有 任何在多边形内的点可以 同时“看到”点 \(\text A, \text B\)。

对于一个相邻 \(\texttt O\) 点的 \(\texttt R\) 点 \(\text P\)，将 \(\text P\) 的两条边延伸至多边形的对面，这样子“圈”出一块区域 \(S\)，想要“看到”\(\text P\) 就必须要求这个点处于 \(S\) 中。

同理，如果同时想要“看到”点 \(\text P_1, \text P_2, \cdots\)，就必须 同时 处于 \(S_1, S_2, \cdots\) 这些区域中。也就是，要求 必须 有所有区域的交集。\(\square\)

为了方便，我们令 \(C_r \gets \texttt R\) 点个数，\(C_o \gets \texttt O\) 点个数。再稍微推导一下，可以发现 \(C_r\) 必须 \(= C_o + 4\)。

对于最基本的只由 \(90^\circ\) 或 \(270^\circ\) 构成的多边形，

就已经有 \(4\) 个 \(\texttt R\) 点了。接下来，不管怎么增加 \(\texttt O\) 点，都需要有一个与之配对的 \(\texttt R\) 点。

设原来多边形的边数为 \(p\)，增加了一个点（相当于一条边）之后边数变为 \(p + 1\)，内角和应为 \(180^\circ \times (p - 1)\)，比起原先增加了 \(180^\circ\)。但是增加的 \(\texttt O\) 点增加的却是 \(270^\circ\)，所以下一次要补一个 \(90^\circ\) 来补差额。\(\square\)

于是，问题就简化为了在 \(L\) 个空中填入 \(\texttt R, \texttt O\)，使得 \(C_r = C_o + 4\) 且没有两个 \(\texttt O\) 相邻（首尾也算相邻）。

首先解一下方程，

\[\begin{cases} C_r &= C_o + 4 \\ C_r + C_o &= L \end{cases} \]

得 \(C_r = \lfloor L \div 2 \rfloor + 2, C_o = \lfloor L \div 2 \rfloor - 2\)。

于是，为了满足题目要求，应要在 \(C_r\) 个 \(\texttt R\) 空隙中插入 \(C_o\) 个 \(\texttt O\)。

分类讨论：

• 开头为 \(\texttt O\)，则结尾不能为 \(\texttt O\)。转换为，在 \(C_r - 1\) 个空中选 \(C_o - 1\) 个。总共有 \(\dbinom{C_o - 1}{C_r - 1}\) 种情况。

• 开头为 \(\texttt R\)，则结尾可以为 \(\texttt O\)。转换为，在 \(C_r\) 个空中选 \(C_o\) 个。总共有 \(\dbinom{C_o}{C_r}\) 种情况。

总共是 \(\dbinom{C_o - 1}{C_r - 1} + \dbinom{C_o}{C_r}\) 种情况。

设 \(L' \gets \lfloor L \div 2 \rfloor\)，化简一下得

\[\begin{aligned} &\dbinom{C_o - 1}{C_r - 1} + \dbinom{C_o}{C_r} \\ = ~ & \dfrac{(C_r - 1)!}{(C_o - 1)! \times 4!} + \dfrac{C_r!}{C_o! \times 4!} \\ = ~ &\dfrac{(L' - 2)(L' - 1)(L')(L' + 1)}{24} + \dfrac{(L' - 1)(L')(L' + 1)(L' + 2)}{24} \end{aligned} \]

在本题极限数据 \(L = 1000\) 下，答案为 \(5208312500\)，直接算即可。

最后不要忘记特判：当 \(2 \nmid L\) 时，没法刚好一个个配对 \(90^\circ\) 与 \(270^\circ\)（上面已经提到过），所以无解输出 \(0\)。代码。