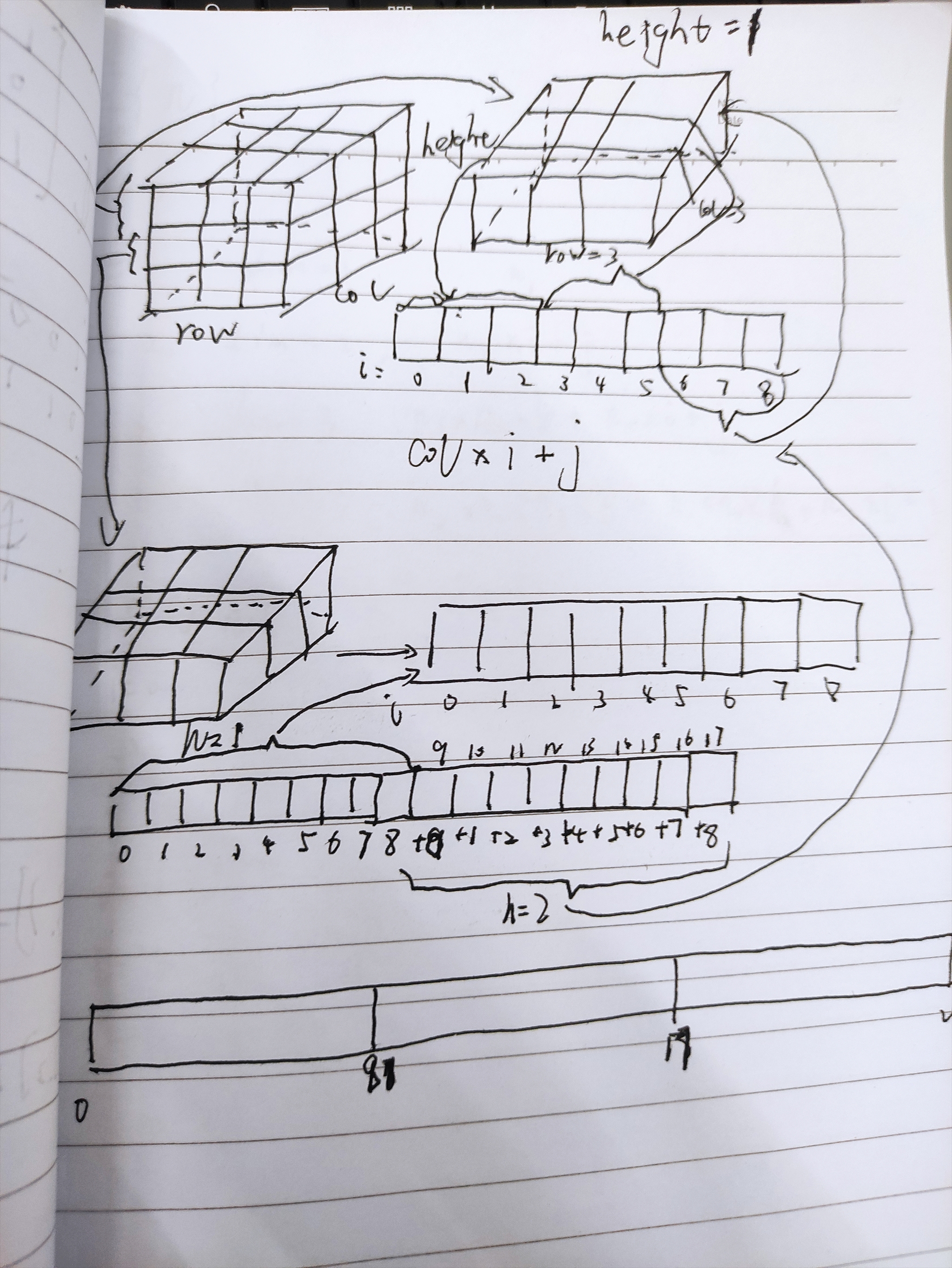
一维数组表示高维矩阵中的变换

二维数组A[rows][columns]放到一维数组B中的对应公式:

两种方式 ：

（1）、按行遍历 

A[i][j] = B[ i + j * rows ]

（2）、按列遍历

A[i][j] = B[ i * columns + j ]

创建一个Array3D类，用一维数组存储三维维数组的数据。

此时我们只需关注“长”、“宽”和“高”的数值，细节交由Array3D来处理，这就是将原始数据类型包装成包装器类型或结构体的优点。

三维数组A[widths][depths][heights]放到一维数组B中的对应公式:
A[i][j][k] = B[ ( i - 1 ) * ( depths * heights ) + ( j - 1 ) * heights + k ]

四维维数组A[a][b][c][d]放到一维数组B中的对应公式:

A[i][j][k][w] = B[(i - 1) * (b * c * d) + (j - 1) * (c * d) + (k - 1) * d + w]

归纳演绎

N维数组映射到一维数组

由此及彼，由表及里，归纳总结，创建一个Dim类，用一维数组存储n维数组的数据，

此时我们只需关注每一个维度的数值，细节交由Dim来处理，这就是将原始数据类型包装成包装器类型或结构体的优点。

深入思考：

(1)、多维度中各维度所表示意义的顺序可以任意确定，确定维度顺序之后，就按照既定的维度顺序进行对一维数组进行读写。

(2)、如同二维数组中可以按照行遍历或者按照列遍历一样。多维数组也可以任意确定多维数组中下标i、j、k、w、...的顺序。

下标顺序确定之后就不可变更，根据下标顺序得出对应公式，公式从上文中请归纳，就按照既定的下标顺序进行对一维数组进行读写。