CodeForce 877E. Danil and a Part-time Job

题目链接

https://codeforces.com/contest/877/problem/E

题意

有一棵 \(n\) 个点的树，根结点为 \(1\) 号点，每个点的权值都是 \(1\) 或 \(0\)

共有 \(m\) 次操作，操作分为两种

\(get\) 询问一个点 \(x\) 的子树里有多少个 \(1\)

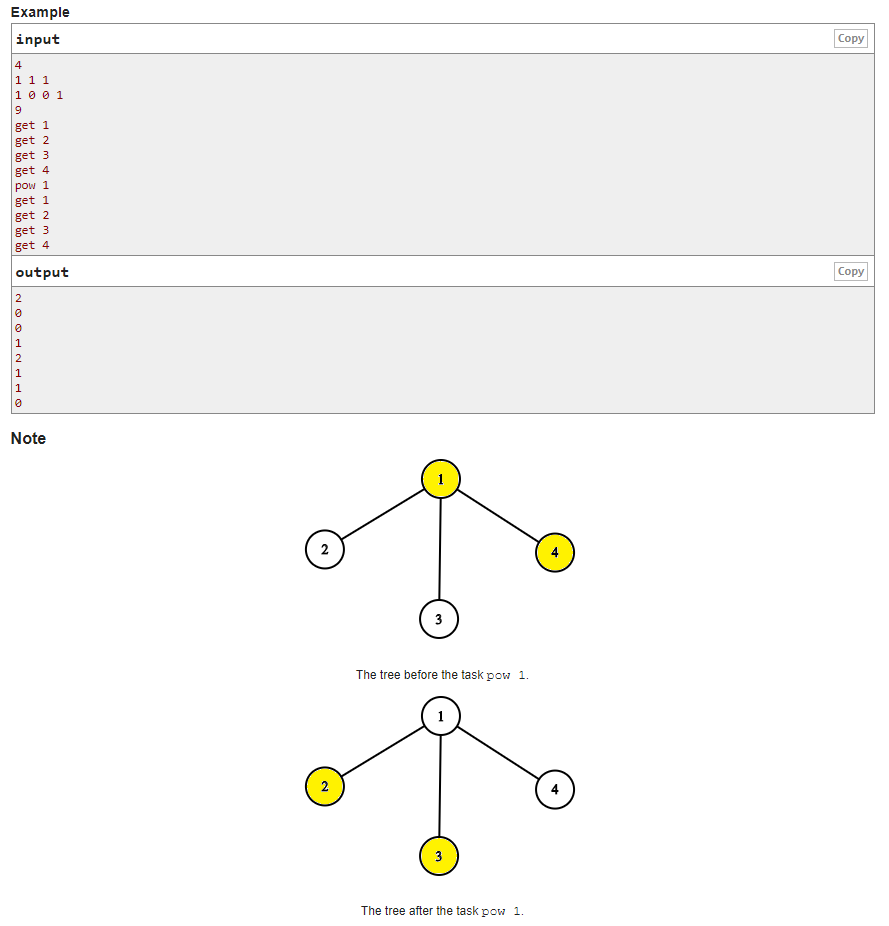
\(pow\) 将一个点 \(x\) 的子树中所有节点取反

对于每个 \(get\) 给出答案

思路

利用DFS序的特性，将每个节点按DFS序建立线段树，可以使得每一棵子树在DFS序上是一段连续的区间， 对于每次更新操作， 用区间大小减去这个区间的和即可实现取反。

AC代码

#include<bits/stdc++.h>
#define ls rt << 1
#define rs rt << 1 | 1
#define lson l , mid , rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define lr2 (l + r) >> 1
using namespace std;
typedef long long ll;
const int maxn = 4e5 + 50;
int sum[maxn << 2], lazy[maxn << 2];
int a[maxn], L[maxn], R[maxn];
void push_up(int rt){
    sum[rt] = sum[ls] + sum[rs];
}
void push_down(int rt, int l, int r){
    int mid = lr2;
    if(lazy[rt]){
        sum[ls] = (mid - l + 1) - sum[ls];
        sum[rs] = (r - mid) - sum[rs];
        lazy[ls] ^= 1;
        lazy[rs] ^= 1;
        lazy[rt] = 0;
    }
}
void update(int a, int b, int l, int r, int rt){
    if(a <= l && b >= r){
        lazy[rt] ^= 1;
        sum[rt] = (r - l + 1) - sum[rt];
        return;
    }
    push_down(rt, l, r);
    int mid = lr2;
    if(a <= mid) update(a, b, lson);
    if(b > mid) update(a, b, rson);
    push_up(rt);
}
void insert(int pos, int val, int l, int r, int rt){
    if(l == r){
        sum[rt] = val;
        return;
    }
    int mid = lr2;
    if(pos <= mid) insert(pos, val, lson);
    else insert(pos, val, rson);
    push_up(rt);
}
int query(int a, int b, int l, int r, int rt){
    if(a <= l && b >= r){
        return sum[rt];
    }
    int mid = lr2;
    push_down(rt, l, r);
    int ans = 0;
    if(a <= mid) ans += query(a, b, lson);
    if(b > mid) ans += query(a, b, rson);
    return ans;

}
int cnt, n;
vector<int> G[maxn];
int d[maxn];
void dfs(int v, int fa){
    L[v] = ++cnt;
    insert(cnt, a[v], 1, n, 1);
    for(auto u : G[v]){
        if(u != fa){
            dfs(u, v);
        }
    }
    R[v] = cnt;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin >> n;
    for(int i = 2;i <= n;i++){
        int x;cin >> x;
        G[x].push_back(i);
    }
    for(int i = 1;i <= n;i++) cin >> a[i];
    dfs(1, -1);
    int q;
    cin >> q;
    while(q--){
        string s;
        int x;
        cin >> s >> x;
        if(s[0] == 'g'){
            cout << query(L[x], R[x], 1, n, 1) << endl;
        }
        else{
            update(L[x], R[x], 1, n, 1);
        }
    }
    return 0;
}