CS 231n 学习笔记 05——课程4.1 神经网络入门之：反向传播

上节课学习了损失函数的定义以及通过损失函数对模型进行参数优化的策略。

变量x，损失为L时，希望求得L关于当前模型W在x处的梯度表达式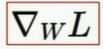

并学习了求解梯度时的两种方法：解析法和差分法

本次课学习使用计算图对任意的初等函数以及一些特殊函数利用反向传播进行梯度求解并应用于参数优化的方法。

 

首先第一个简单的例子：

使用微积分可以很容易求得 f 关于x，y，z的偏导数表达式，代值即可求出梯度值。

分部地看这个式子，令 q = x + y ，则有 f = qz， 即：

和

 

 

我们最终的目的是得到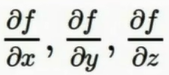这三个量，而由链式求导法则有

产生了一个基本思路：可以将函数 f 分解为多个计算单步计算的拓扑有序集合，将 f 关于各参数x，y，z....的偏导按单步计算。

对于 f =( x + y ) * z 可以产生如下计算图（例中赋值为x=-2,y=5,z=-4）:

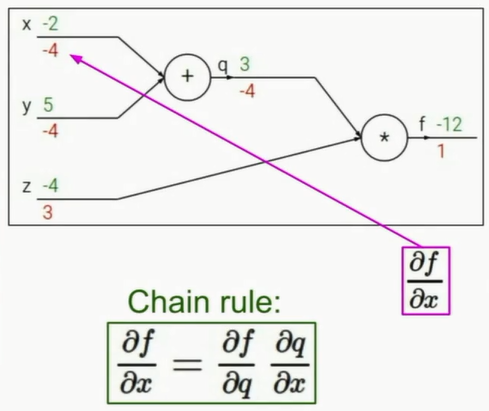
计算图表明了反向传播的基本思路：将初始返回的梯度设置为1，返回时根据遇到的节点的计算规则确定往前进一步传播的梯度值，逆拓扑有序地计算（拓扑有序是在正向传递计算时）各节点对应梯度值，最后到达最初各变量。

图中第一个节点乘法节点，其梯度具有交换的性质，所以向下传递的梯度是上方正向输入的值3，记为z的梯度，向上传递的是z的输入值-4。随后是加法节点，其性质是偏导数为1，即按传入的值传出，所以x，y的梯度都是-4。

需要明确的是，初始传入梯度 1 是为了方便计算，得到和输入对应的相对性质的梯度比例，并不是真正的梯度值。因为对于参数优化而言，每次改变的步长steplength是超参数，此处求得各变量的梯度最终都是为了得到按步长改变参数的方向向量。

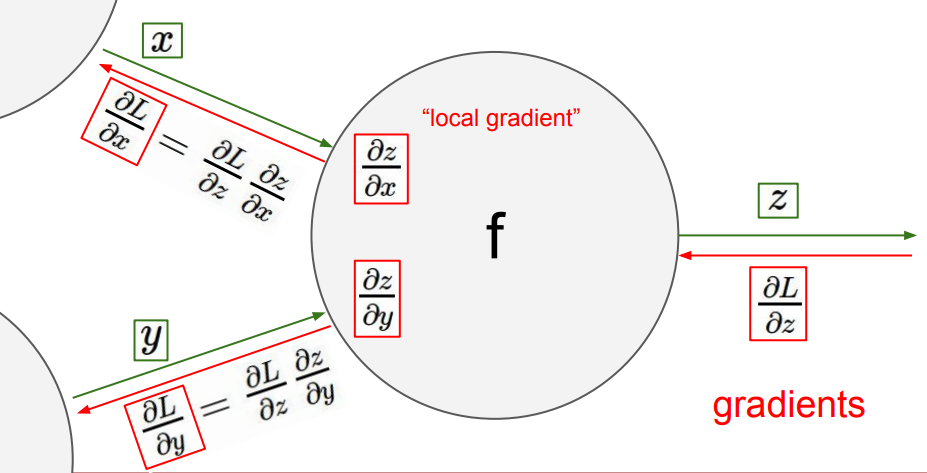
这是一个标准的计算图结点，根据链式法则不断将传入的梯度乘上此时局部的偏导值，得到进一步传回的梯度，即是反向传播。

 

再举一个复杂点的函数为例：

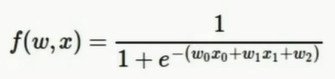
函数变量是W0，W1，W2，X1，X2 

设定一套输入值后，得计算图如下：

取其中几步说明计算步骤:

1.

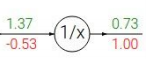
这一步的函数式：f = 1/x  x=1.37, f ' = - 1/x^2

所以返回梯度为 -1/(1.37^2) * 1.00= -0.53，这里要注意代入梯度表达式的是正向的输入值x=1.37

 

2. 

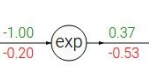
f = e^x  f ' = e^x

返回梯度为  -0.53* e^(-1) = -0.2 ,此处注意输入梯度是-0.53，所以最后按比例计算的返回梯度值是乘-0.53的

 

对于一些特定结构的函数，可以将其当做一个门（Gate），讲这部分计算合并，简化计算图。

如图中的Sigmoid Gate，函数式为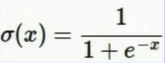，其导数等于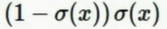

所以上图还可以按1.00 * （1 - 0.73）* 0.73 = 0.2 计算（注意式中是σ(x)即函数值而不是变量值，取右边绿值0.73）

总之对于简单的数个节点，可以按需进行简化。

 

PS1：Max 门（Gate）的计算方式是：将传入梯度返回到大的那一方，另一方梯度取0。

　　　　这是由于正向传递时仅有大的那一方被取到随而影响到了后续的计算

PS2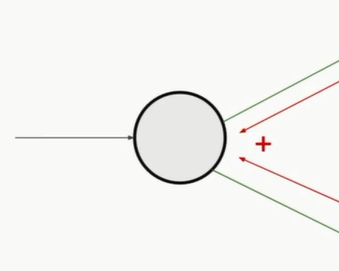：，此类节点在返回梯度时取不同方向传回来梯度之和，再按单值函数算传出梯度。

 

实际中输入值不是单值，而是矩阵和向量（比如 f = Wx是个矩阵乘法），所以返回梯度变为一个矩阵，必须考虑到节点输出所有值受输入所有值的影响，所以返回矩阵是一个雅各比矩阵。

普适的计算思想在我复习线代并推导后回来补充，这里还没想通，仅列出以下算例：

 

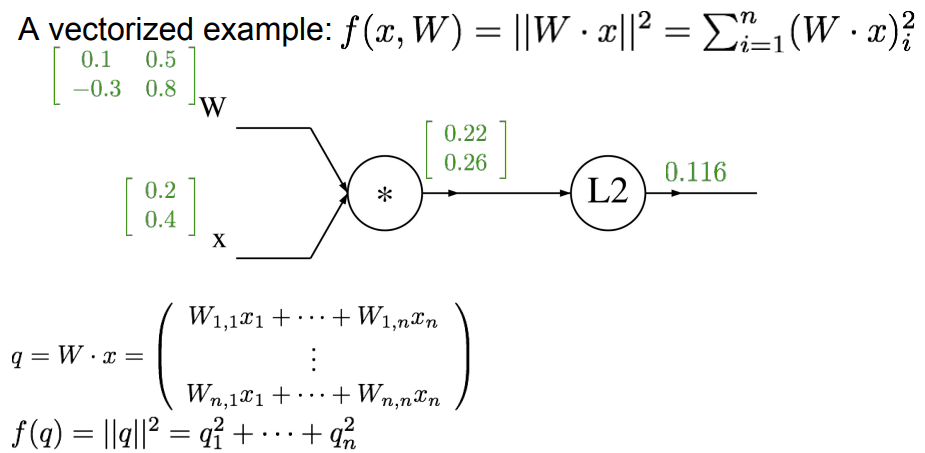
上面f（W，x）经历两步运算：1.矩阵乘法，2.L2取模

按反向传播的顺序：

1. L2 的梯度传回

　　L2计算过程是把一个向量中的每个值平方后求和，f值对输入向量中的每个元素的偏导数，本质上还是平方项的导数。所以梯度表示如下：

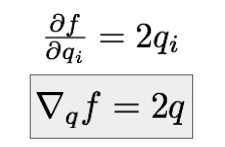　　　得    

 

 2. 矩阵乘法的梯度

　　f = L2（Wx） 

　　推导待补充，公式如下：

　　

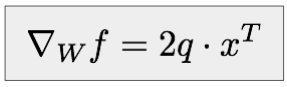
　　需要注意的是，有矩阵参与运算后，各方向返回的梯度值也一定是和输入值相同的矩阵，每个梯度元素表示此位置的元素对输出的影响大小。

 

模块化的计算图实现

一个类型的计算结点，其工作方式是固定的。于是在构造神经网络时可以将其提前模块化，只需为程序提供API

一个典型模块构成如下：

类里包含两个函数，一个是前向传播的计算函数，一个是反向传播的求梯度函数，神经网络的训练就围绕着这两个函数进行。

现有很多开源的神经网络包，其大部分的内容就是计算节点的定义文件，比如Caffe，可以在GitHub上下载使用。