C1005 进行一个三角的查询题解

• 题目描述

  平面上有 $n$ 个点 $(X_i,Y_i)$。

  现在有 $q$ 个询问，每次给定三个点 $A(x + d, y), B(x, y), C(x, y + d)$，回答有多少个点 $(X_i,Y_i)$ 在这个三角形的边界或者内部。

  输入格式

  第一行，两个整数 $n,q$。

  接下来 $n$ 行，每行两个整数 $X_i,Y_i$，表示点的坐标。

  接下来 $q$ 行，每行三个整数 $x,y,d$，表示一个询问。

  输出格式

  输出 $q$ 行，每行一个整数，表示答案。

  ---

  40pts

  直接暴力即可。由于题目时限有 10s，直接 $n^2$ 枚举，能够获得 $40$ 分。

  我下面程序使用二分先直接锁定到了三角形的 $x$ 范围，并没有改善理论复杂度，甚至理论复杂度多了一个 $log$，但在测试中能把程序速度优化 8s 左右。和直接 $n^2$ 枚举分数一样，均为 $40$ 分。

  #include <iostream>
  #include <cstdio>
  #include <algorithm>
  #define INF 0x7fffffff
  #define MAXN 1000005
  #define eps 1e-9
  #define foru(a,b,c)	for(int a=b;a<=c;a++)
  #define RT return 0;
  #define LL long long
  #define LXF int
  #define RIN read_32()
  #define HH printf("\n")
  #define GC (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?0:*p1++)
  using namespace std;
  char buf[1<<20],*p1,*p2;
  inline int read_32(){LXF X=0,w=0;char ch=0;while(ch<'0'||ch>'9'){w|=ch=='-';ch=GC;}while(ch>='0'&&ch<='9') X=(X<<3)+(X<<1)+(ch^48),ch=GC;return w?-X:X;}
  int n,q;
  class Pos{
  	public:
  		int x,y;
  		bool operator < (const Pos _x)const{
  			return this->x<_x.x;
  		}
  		Pos(int _x=0,int _y=0):x(_x),y(_y){
  			
  		}
  }a[MAXN];
  signed main(){
  	n=RIN,q=RIN;
  	int x,y,d,ans;
  	for(int i=1;i<=n;i++){
  		x=RIN,y=RIN;
  		a[i]={x,y};
  	}
  	sort(a+1,a+1+n);
  	for(int i=1;i<=q;i++){
  		x=RIN,y=RIN,d=RIN,ans=0;
  		int bg=lower_bound(a+1,a+1+n,Pos(x,y))-a;
  		int ed=upper_bound(a+1,a+1+n,Pos(x+d,y))-a;
  		for(int j=bg;j<=ed;j++){
  			if(a[j].y>=y && a[j].y<=-a[j].x+x+y+d){
  				ans++;
  			}
  		}
  		printf("%d\n",ans);
  	}
  	return 0;
  }
  

  100pts

  我们先来画个图，把询问的三角形画出来。

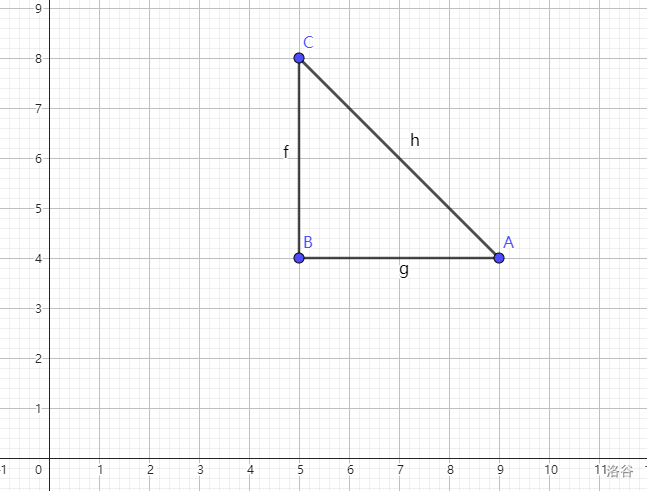
我们就是要询问在这个三角形内的点的数量对吧？

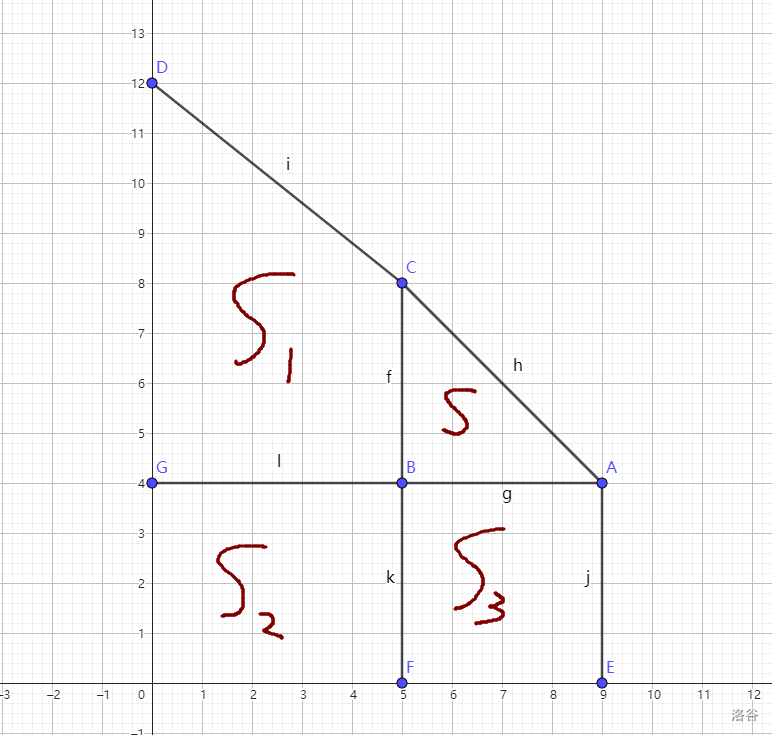
把它补成这样一个梯形，那么就会有：

$$S=S_{大梯形}-S_{直线CF左侧部分}-S_3$$

又因为 $S_3$ 可以表示成这个：

$$S_3=S_{A点左下方}$ $- S_{B点左下方}\\ =(S_2+S_3)-S_2$$

所以：

$$S=S_{大梯形}-S_{直线CF左侧部分}-\left[(S_2+S_3)-S_2\right]\\ =S_{大梯形}-S_{直线CF左侧部分}-(S_2+S_3)+S_2$$

那我们该怎么做呢？我们把这四“项”分两次解决，第一次解决$S_{大梯形}-S_{直线CF左侧部分}$，第二次解决 $-(S_2+S_3)+S_2$。

观察 $S_{大梯形}$ 和 $S_{直线CF左侧部分}$，他们俩都是个梯形，而且斜着的那条边所在的直线相同。

观察 $(S_2+S_3)$ 和 $S_2$，他们俩都是个矩形，而且顶部的那条边所在的直线相同。

这就可以扫一遍解决了。

具体地，为了解决前两项，我们先把所有点按照以下规则排序：

按照 "过这个点的，斜率为 $-1$ 的直线与 $y$ 轴交点的纵坐标大小" 升序。

比较抽象？其实很简单，画个图就懂了。

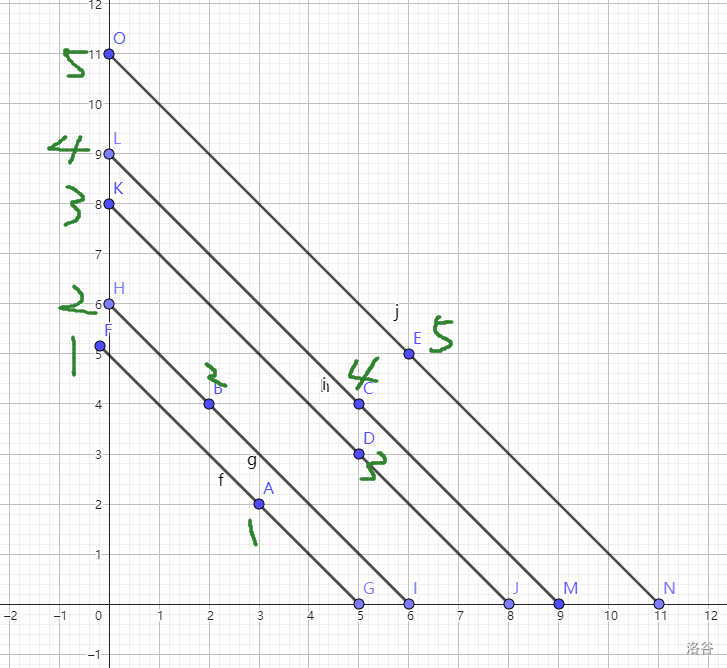
排序完就是按照绿色数字顺序访问这些点的。

这样有什么好处？比如我们访问到第四个点 $C$ （与原题的字母标号无关）的时候，发现它斜下方的点都已经访问过了。换句话说，如果我问你 $C$ 斜下方有几个点，你能很轻松的回答出来，前面的都是嘛！

这里说的“斜下”其实不严谨，应该是 $C$ 所在的斜率为 $-1$ 直线下方的点。即直线 $ON$ 下方的点。说"斜下"只是为了直观理解。

但我们刚才分析出来的四块面积里没有三角形啊？这是干嘛呢？我们不是想要梯形吗？

我们刚才之所以只能回答在斜下方的三角形里有多少点，是因为我们只是开了一个变量来记录。我们开个桶不就行了？

我们模仿树状数组求逆序对时的思路，在值域上开个树状数组。访问到一个点的时候，我们就把它的横坐标的地方在桶里 $+1$，这样我们用树状数组查询前缀和的时候，就可以查询任何位置左侧点的数量了。

比如在上图中，我们已经访问到了 $C$，那么 $A,B,D$ 都应该已经插入了树状数组。这时候我们 $ask(4)$ ，意思就是获取横坐标小于等于 $4$ 的点的数量，自然就知道是 $2$ 了。

发现什么？这不就截出来梯形了吗？

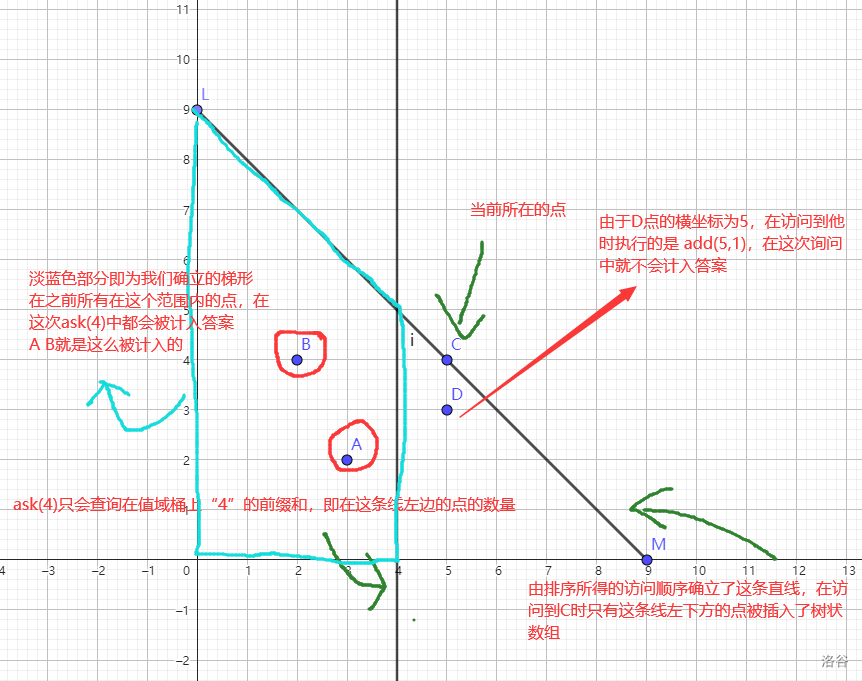
OK，我们马上就要解决查询梯形的问题了。我们到目前为止只是对所有的点排了序，我又不是问点，我是问三角形，咋办？

还是这张图：

虽然 $ABC$ 这个三角形是个询问，但我们可以把这个询问伪装成一个点，和题目中的点混在一起。相当于，我们随便选了 $A,C$ 中的一个点，之所以可以随便选是因为他们都在 $AC$ 上，然后把他混进输入的点中排序，但得给它留一个“我其实是询问”的标记。

以选 $A$ 来伪装为例，当我们访问到 $A$ 时，直线 $AC$ 下方的所有点已经被插入了树状数组，我们只需要 $ask(x_A)$ 就能得到 $S_{大梯形}$ ，$ask(x_C)$ 就能得到$S_{直线CF左侧部分}$。

但这样发现很难实现。我们把 $A$ 自己混进去了，倒时候去哪里找 $C$ 呢？

所以我们换种“伪装”，大体思想是一样的。我们把所有点 $(x,y)$，看成是一组 $x,y,0$ 的询问，然后把他们全混一起。排序的时候，不能按照 $x+y$ 排序，而是按照 $x+y+d$ 排序。具体这个式子是怎么来的，请读者自行把点坐标带入一次函数解析式来理解。

这样，对于所有的点，排序的时候凭据是过它的那条斜率为 $-1$ 的直线，而对于所有的询问，我们在保留所有信息的同时，以它的斜边所在的直线作为排序凭据。

注意排序会打乱顺序，所以我们要记录原本的序号 $id$，方便我们输出。这也正好可以用来在遍历时辨别到底访问的是个点还是个询问。

这部分代码+读入部分代码：（ $C$ 是树状数组，比如修改就是 $C.add(x,k)$，$ans$ 是答案数组，$RIN$ 是快读，$Pos$ 存询问）

bool cmpB(Pos x,Pos y){
	int b1=x.x+x.y+x.d;
	int b2=y.x+y.y+y.d;
	return b1<b2 || (b1==b2 && x.id<y.id);
}
int ans[MAXN];

signed main(){
	n=RIN,q=RIN;
	int x,y,d;
	for(int i=1;i<=n;i++){
		x=RIN,y=RIN;
		a[i]=Pos(x,y,0,0);
	}  
	for(int i=1;i<=q;i++){
		x=RIN,y=RIN,d=RIN;
		a[i+n]=Pos(x,y,d,i);
	}
	sort(a+1,a+1+n+q,cmpB);
	for(int i=1;i<=n+q;i++){
		if(a[i].id==0)	c.add(a[i].x,1);
		else{
			ans[a[i].id]+=c.ask(a[i].x+a[i].d)-c.ask(a[i].x-1);//加上大矩形，减去CF"左侧"的面积。
		}	
	}
    ......
}

如果问为什么有个 $c.ask(a[i].x-1)$，是因为树状数组返回的是前缀和，是小于等于的数量。可结合前缀和的 $S_r-S_{l-1}$ 来理解，一个道理。如果后一个ask不减1，所有在直线CF上的、理应算在三角形的点也会被错误地删去。

---

下面来解决那俩矩形的问题。即 $(S_2+S_3)$ 和 $S_2$。甚至更简单了，我们只需要把所有混起来的点和询问按照纵坐标排序即可。这样访问到某个点/询问时，其下方的点已经全部被插入树状数组。

直接给出这部分+输出的代码：

bool cmpY(Pos x,Pos y){
	return x.y<y.y || (x.y==y.y && x.id>y.id);
}
signed main(){
    .....
    sort(a+1,a+1+n+q,cmpY);
    for(int i=1;i<=n+q;i++){
        if(a[i].id==0)	c.add(a[i].x,1);
        else{
            ans[a[i].id]-=c.ask(a[i].x+a[i].d)-c.ask(a[i].x-1);
        }	
    }
    for(int i=1;i<=q;i++){
        printf("%d\n",ans[i]);
    }
}

有个细节，$cmpY$ 里写的是 $x.id>y.id$。这是为什么呢？

我们是钦定所有点的 $id$ 为 $0$ 的，这个语句的意义也就是：当纵坐标相同时，优先访问完所有这个高度的询问，再访问这个高度的点。

这与先访问点再访问询问有何不同呢？如果我们先访问点，那么在访问相同高度的询问时，与询问同高的点也被加入了树状数组。这就会导致错误。

比如 $B$ 是个询问。我们假设 $AB$ 上有某个题目输入的点 $K$，如果我们先访问相同高度的点，即先访问点 $K$，那我们在处理询问 $B$ 的时候，$-(S_2+S_3)+S_2=-S_3$，会把 $K$ 也算进 $S_3$ 扣除掉，这显然不是我们想要的，$AB$ 上的点是要计入答案的，怎么能被扣除掉呢？

这一块代码中也出现了 $c.ask(a[i].x-1)$，道理和刚才是一样的，我们是想要 “$BF$ 左侧” 点的数量，而不是 ”$BF$ 上 + 左侧“ 点的数量。

至此整个题目结束。由于 $n,q$ 同级，复杂度是 $O(nlogn)$ 的。

注意树状数组值域要开到 $2\times 10^6$，因为有可能会 $ask(x+d)$，这两个都是 $1\times 10^6$ 级别的。

完整代码：

#include <bits/stdc++.h>
#define INF 0x7fffffff
#define MAXN 1000005
#define eps 1e-9
#define foru(a,b,c)	for(int a=b;a<=c;a++)
#define RT return 0;
#define LL long long
#define LXF int
#define RIN read_32()
#define HH printf("\n")
#define GC (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?0:*p1++)
using namespace std;
char buf[1<<20],*p1,*p2;
inline int read_32(){LXF X=0,w=0;char ch=0;while(ch<'0'||ch>'9'){w|=ch=='-';ch=GC;}while(ch>='0'&&ch<='9') X=(X<<3)+(X<<1)+(ch^48),ch=GC;return w?-X:X;}
int n,q;
class Pos{
	public:
		int x,y,d,id;
		Pos(int _x=0,int _y=0,int _d=0,int _id=0):x(_x),y(_y),d(_d),id(_id){
			
		}
}a[MAXN<<1];
inline int lb(int x){return x&-x;}
class Tree{
	private:
		int c[MAXN<<1];
	public:
		void add(int x,int k){
			for(;x<=2000000;x+=lb(x)){
				c[x]+=k;
			}
		}
		int ask(int x){
			int ret=0;
			for(;x;x-=lb(x)){
				ret+=c[x];
			}
			return ret;
		}
		void clear(){
			memset(c,0,sizeof c);
		}
}c;
bool cmpY(Pos x,Pos y){
	return x.y<y.y || (x.y==y.y && x.id>y.id);
}
bool cmpB(Pos x,Pos y){
	int b1=x.x+x.y+x.d;
	int b2=y.x+y.y+y.d;
	return b1<b2 || (b1==b2 && x.id<y.id);
}
int ans[MAXN];

signed main(){
	n=RIN,q=RIN;
	int x,y,d;
	for(int i=1;i<=n;i++){
		x=RIN,y=RIN;
		a[i]=Pos(x,y,0,0);
	}  
	for(int i=1;i<=q;i++){
		x=RIN,y=RIN,d=RIN;
		a[i+n]=Pos(x,y,d,i);
	}
	sort(a+1,a+1+n+q,cmpB);
	for(int i=1;i<=n+q;i++){
		if(a[i].id==0){
			c.add(a[i].x,1);
		}else{
			ans[a[i].id]=ans[a[i].id]+c.ask(a[i].x+a[i].d)-c.ask(a[i].x-1);//+大梯形-小梯形
		}	
	}
	c.clear();//具体实现见class，就是个memset。
	sort(a+1,a+1+n+q,cmpY);
	for(int i=1;i<=n+q;i++){
		if(a[i].id==0){
			c.add(a[i].x,1);
		}else{
			ans[a[i].id]=ans[a[i].id]-c.ask(a[i].x+a[i].d)+c.ask(a[i].x-1);//-大矩形+小矩形
		}	
	}
	for(int i=1;i<=q;i++){
		printf("%d\n",ans[i]);
	}
	return 0;
}