CF/505/D 题解

思路

---

这道题的思路其实是根据样例图片来的。

首先第一张：

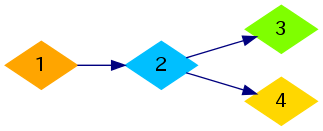
这张图片可以得知 $ n $ 个点没有环的时候最少需要 $ n - 1 $ 个点。

再看第二张：

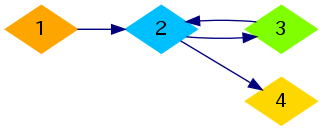
这个图确实很难思考，但稍微思考一下如果我们把含有一个强连通分量的图变成一整个强连通图。

这个图的边数不就变成 $ n $ 了吗？

来推一下为什么这样最小：

因为强连通块需要的边数为 $ n $ 把他所在的图变成一个强连通图之后就是最小的了因为这个图中所有点都能互相到达了且只需要点的个数条边。

所以边数的数量就是含有强连通块的数量的图的点数之和，加上，没有含有强连通块的图的点数数量没有含有强连通块的图的数量。

因为每一个没有强连通分量需要点数个数 $ -1 $ 条边而含有强连通分量的图需要点数个数条边，因此我们可以得出最少需要的边数总点数的数量减去没有强连通分量图的数量。

这些问题解决了的话基本就好了，强连通块的数量就用 tarjan 求就行了。

AC 代码：

#include <bits/stdc++.h>
#include <map>
#include <bitset>
#define ll long long
#define prt printf
#define sc(ppt) scanf("%d" , &ppt)
using namespace std;
 
const int maxn = 1e5 + 1;
map<int , map<int , int>> G; // map来去重边 
int ans1 , ans2 , n , m , bj = 0; //题目需要 
int U[maxn] , V[maxn] , Cnt = 0 , cnt = 0 , H[maxn] , h[maxn]; //链式前向星 
int vis_d[maxn] ; // dfs
int sum , deep = 0 , top = 0 , dfn[maxn] , low[maxn] , vis[maxn] , stk[maxn] , color[maxn] , num[maxn]; // tarjan
struct edge{
	int next , to;
}e[maxn],e_d[maxn];
 
void add_edge(int u , int v){
	++cnt;
	e[cnt].next = h[u];
	e[cnt].to = v;
	h[u] = cnt;
} //tarjan 
 
void add(int u , int v){
	++Cnt;
	e_d[Cnt].next = H[u];
	e_d[Cnt].to = v;
	H[u] = Cnt;
} //缩点后 
 
void tarjan(int u){
	dfn[u] = ++deep , low[u] = deep , vis[u] = 1 , stk[++top] = u;
	for(int i=h[u] ; i ; i=e[i].next){
		int v = e[i].to;
		if(!dfn[v]){
			tarjan(v);
			low[u] = min(low[u] , low[v]);
		}
		else{
			if(vis[v]) low[u] = min(low[u] , dfn[v]);
		}
	}
	if(low[u] == dfn[u]){
		++sum;
		int v;
		do{
			v=stk[top--];
			vis[v] = false;
			color[v]=sum;
			num[sum]++;
		}while(u != v);
	}
} //板子 
 
void dfs(int u){
	vis_d[u] = 1;
	if(num[u] >= 2 && bj == 0){
		++ ans1;
		bj = 1;
	} //判断是否有强联通分量 
	for(int i=H[u] ; i ; i=e_d[i].next){
		int v = e_d[i].to;
		if(vis_d[v] != 1){
			dfs(v);
		}
	}
} //判断树 
 
signed main(){
	sc(n) ; sc(m) ;
	for(int i=1 ; i<=m ; i++){
		int u , v;
		sc(u) ; sc(v) ;
		U[i] = u;
		V[i] = v;
		add_edge(u , v);
	}
	for(int i=1 ; i<=n ; i++) if(!dfn[i]) tarjan(i);
	for(int i=1 ; i<=m ; i++){
		if(G[color[U[i]]][color[V[i]]] == 1 || color[U[i]] == color[V[i]]) continue;
		add(color[U[i]] , color[V[i]]);
		add(color[V[i]] , color[U[i]]);
		G[color[U[i]]][color[V[i]]] = 1;
	} //存双边变成树
	for(int i=1 ; i<=sum ; i++) {
		if(!vis_d[i]){
			bj = 0;
			++ans2, dfs(i);
		}
	} // 看有几棵树 
	prt("%d" , n - ans2 + ans1); // 数的数量 - 含有强连通树的数量就是没有强联通树的数量
	return 0;
}