计算机组成原理学习笔记_计算机运算方法
计算机运算方法
1.有符号数与无符号数：
无符号数就是没有符号的一个数，即不存在负值，一个n位2进制无符号数其表示范围为0~2^n-1,即从全零到全一。
有符号数，这个数存在征服号，一个有符号数包含一个符号部分和一个数值部分，一个n位2进制有符号数，首位为符号位占一位，数值位占n-1位，符号位0为正，1为负。
1.真值：就是一个带符号的数，比如二进制数：+1001，-0001，+0.1001或十进制数+10，-99都是真值。
2.机器数：将符号数字化的数。计算机当中只包含0和1，没有+和-，于是将0和1代替符号，符号位一般是放在最高位。
1.原码表示：一个二进制真值+x的原码，+x是正数那么原码就为数x的数值部分前面加上个0代表符号，即0x。如果是负数,即真值为-x的原码就是2^n-（-x）（其中n为原码的位数，-x为真值），即加上符号位1。
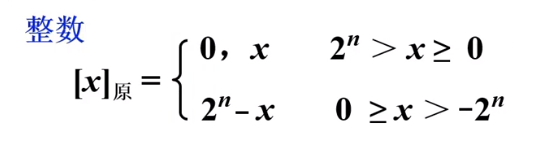（其中n为原码的位数）
2.反码表示：反码是在原码基础上变换，正数的反码与原码相等，负数的反码等于原码的数值位取反，0变1，1变0。
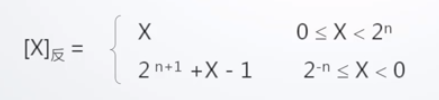
3.补码表示：补码的表示，正数的补码就是其原码本身，负数的补码是其反码加一。比如+1001的补码是01001，-1001的补码是10111。
为什么需要补码：补码解决了二进制减法的问题将二进制减法问题转换为了加法问题，比如A-B转换为A+（-B）。即用加法器就可以实现加减的运算。
补码的本质：
对于二进制数在计算机内储存是有范围的，超出范围之后就会归零，比如储存4位二进制，当数值到1111时，我们再加一变成10000发生溢出，由于只能存储4位，故将最高位抛弃，变为0000。
对于这个模型就是我们生活中常见的时钟，时钟最大值时针最大为23，当时针到达24时一圈结束，时间归零。
时钟模型中，如果当前时间是凌晨1点，求往后3小时是几点，我们将时针往后拨3段就可以得到4点。
那么要求往前3小时是几点，我们有两中计算方法，第一，我们可以将时针往前拨3段是22点，第二我们将时针往后拨21段，得到22点。
我们可以看出来，第一种方法是减法，第二种方法是加法。补码运算就是摒弃第一种方法，使用第二种方法。
上面的21就是3对24的补码，也就是说将减法转换为加上减数的补码。
回到二进制数中，求补码，对于一个负的4位二进制数X，我们要求他的补码，我们就需要找到一个四位二进制数Y，使得X+Y=10000（或0000），我们会发现求出这个Y需要对X做减法，也就是需要借位，为了避免这个问题，我们可以把式子转换一下：X+Y-1=10000-1→X+Y-1=1111，我们发现当等号右边的数变为全一的时候，无论X是啥数我们都不需要借位，并且1111-X得到的数刚好是X的反码，即1-1变成了0，1-0变成了1，最终得到：Y-1=1111-X即Y=X的反码+1。至此补码通过一个类似于溢出的机制，将二进制数中的加减法，全部变成了加法。实现了简便的运算。
4.移码表示：再利用补码比较大小时会出现，不容易比较的情况，就需要移码。补码负数由于符号位为1，则由于二进制表示，负数于正数比较大小的时候总是负数大于正数。
对于一个真值x，无论正负数，x的移码都是x加上2^n（n是x的位数）
比如+1001的移码就是1001+10000（2^5）=11001。-1001的移码就是-1001+10000=00111。对比补码，移码其实就是将补码的符号位取反。
2.数的定点表示和浮点表示：
1.定点表示：小数点按约定方式标出。 即在设计的时候就将小数点的位置固定好。
2.浮点表示：浮点数表示就是利用科学计数法的形式来表示一个小数。公式为
其中N是浮点值，S是尾数，r是尾数的阶值，j是阶码。
打个比方 1.25*10^8 其中1.25就是尾数，10就是阶值，8就是阶码。计算机中阶值一般是2。尾数S是小数，j阶码可正可负。
计算机中的表示方法。
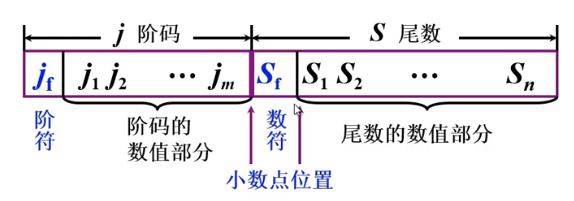
浮点数规格化:
对于一个用上述公式表示的浮点数来说，一个小数可以有很多种表示方法。例如对十进制表示的12有1.2*10^1,还有0.12*10^2等等。我们需要一个标准的格式来记录。
对于阶值为2的浮点数表示，尾数的小数部分的最高位为1。例如0.000101表示为0.101*2^11(二进制的3)
如何规格化：
尾数左移一位，阶码减一
尾数右移一位，阶码加一
直到尾数最高位为1。
IEEE754标准：
IEEE754是标准定义了表示浮点数的格式。
S为尾数数的符号位0位正，1为负。
后面跟着阶码，采用偏移量为127的移码，即原值加上127为新值。以方便对浮点数的排序。
尾数是规格化的浮点数。规格是最高的有效位为1。也就是说把小数点左边变为1，储存的时候省略最高为有效的1。
如果是单精度即转换成
E=0，M=0；表示机器0
E=255，M=0；表示无穷大。
E=255，M！=0；表示Nan，一个非数字，即0/0；
IEEE754有两种格式分别是32位和64位。
举例 浮点数真值与IEEE754单精度浮点数转化：
将20.59375转换成浮点数。
1.将十进制转二进制小数：20.59375=10100.10011
2.将二进制小数转换为1.M的形式，将小数点左移4位即：1.010010011*2^4
3.求出各个IEEE754中各个数值的大小：符号位（1位）为S=0，阶码（8位）为00000100，E=00000100+01111111（127）=10000011，尾数M（23位）为010010011000....000。
4.计算机储存为 010000011010010011000......00（共32位）
IEEE754单精度浮点数还原为真值：
有010000011010010011000......00（共32位）
1.按照格式取第一位为符号位S=0，第2-9位为阶码10000011，尾数M为010010011000....000。
2.将阶码还原 即阶码-127 10000011-01111111=00000100（2）=4（10）。
3.将尾数还原为1.010010011000....000。
4.得到+1.010010011000....000*2^4=10100.100110000....0000
5,转换为10进制：20.59375。
数据运算：
1.定点数加减法运算：
设有真值A和B。
加法：A+B有[A]补+[B]补=[A+B]补（mod2n+1）在模运算基础上实现。
即输入了两个数，首先变成补码，在进行加运算。比如键盘输入18和-21，真值为+10010和-10101，补码为010010和101011，求和为111101，在将机器数转换为真值，-00011即-3。
减法：[A-B]补=[A]补-[B]补=[A]补+[-B]补。
补码将减法转换为加法。不需要再设计减法器。
我们需要做的就是用B的补码去求-B的补码。
B是18，真值为+10010，补码为010010，
-B是-18，真值是-10010，补码为101110。
即补码变化就是B的补码从右开始找到第一个1，第一个1的左边取反，右边和本身不变的输出。
2.溢出检测：
当计算出的数超过了数据表示的范围，就是溢出了。
1.当两个负数加运算得出正数，或两个正数加运算产生正数，就会产生溢出。检测溢出就可以用参与运算的数的符号和结果符号做比较。如果符号出现了上述情况则为溢出。
参与运算的数符号X0 Y0和结果符号S0 V为是否溢出，V=0为溢出。
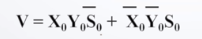
2.对最高数据位的进位位和符号位比较。
符号位进位C0，数据最高位进位C1
V=C0 异或C1
3.用变形补码（双符号位）
将数的符号位变为两位。再计算的时候正常情况下，两个数符号都是一样的为00或11，如果发生溢出则符号位会变化。再输出数据的时候用模2n+2 来获得一位符号的数据。
3.原码的一位乘法：
原码的一位乘法基于加法和竖乘运算，
再进行竖乘运算的时候，我们每次进行一次乘法过后都会进行一次加法，来获得一个累加的结果。再二进制中同样适用，再进行乘法的时候要注意将符号位单独运算，数据部分去绝对值参加运算。
由于竖乘做加法时，会出现这样的情况。
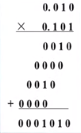
即需要2n位寄存器来储存结果，每次相加的值都会较之前左移一位。
改进方式:在每次得到一个加数时，对其进行右移，得到部分积（红色部分），通过累加的方式来求和，得到和之后对和进行右移操作，并把右移出去的数字放入乘数寄存器中。最后得到的结果一部分再乘数寄存器中（红色部分），一部分再乘法器中（黑色部分）
总的来说，原码乘法就是每次根据乘数来判断部分积是加上0还是加上被乘数。
4.补码的一位乘法：
对于补码乘法，符号位直接参与运算。
有真值A=+1101，B=+1011。求A*B，A为被乘数，B是乘数。
补码乘法有如下操作:
计算被乘数A的补码[A]补=01101和[-A]补=10011。计算乘数的补码[B]补=01011，设部分积为0。
根据如下规则：
(1) 如果 Bn = Bn+1 ，部分积加0，再算术右移一位；
(2) 如果 Bn Bn+1 = 01，部分积加被乘数的补码[A]补，再算术右移一位；
(3) 如果 Bn Bn+1 = 10，部分积加上被乘数负数的补码[-A]补，再算术右移一位；
其中n为乘数的位数，那么Bn+1则是再最后一位后补0。
算术右移，正数最高位补0，负数最高位补1。
拿出乘数补码01011补n+1位有
乘数：010110 取n和n+1位为10，则部分积加上[-A]补10011，部分积=10011，部分积算术右移一位得到11001，移出的一位补到乘数最高位上。即乘数010110->101011。
乘数：101011 取n和n+1位为11，则部分积加0，部分积为11001，部分积算术右移一位得到11100，移出的一位补到乘数最高位上。即乘数101011->110101。
乘数：110101 取n和n+1位为01，则部分积加上[A]补01101，部分积为01001，部分积算术右移一位得到00100，移出的一位1补到乘数最高位上。即乘数110101->111010。
乘数：111010 取n和n+1位为10，则部分积加上[-A]补10011，部分积为10111，部分积算术右移一位得到11011，移出的一位1补到乘数最高位上。即乘数111010->111101。
乘数：111101 取n和n+1位为01，则部分积加上[A]补01101，部分积为01000。
至此我们乘数的所有位数都用到了，及乘数所有非新增位皆参与运算，之后运算结束。此时部分积为01000，移出位为1111，得到[A*B]补=010001111，再将其转换为真值，为+10001111即143=13*11。
5.定点数除法：
通过乘法，我们直到乘法是通过加法实现的，对于除法，便通过减法实现，对于手工减法，每次判断被除数剩下的值能否够减除数来进行除法的。
1.恢复余数法：
有被除数X除数Y。要计算X/Y。余数为Q。
符号位单独计算。取异或结果。
首先计算Q=X-Y，如果Q<0则说明X<Y,商上0，余数恢复，则Q=Q+Y，再对余数进行逻辑左移一位操作。如果Q>0则商上1,并对余数进行逻辑左移一位操作。
之后每次让余数Q去减去除数Y得到一个新余数Q，如果得到的余数大于0则商上1并将Q左移，如果得到的余数小于零，则需要恢复余数，即加上除数Y，并将Q左移一位。
重复直到到达商所需要得位数即可。
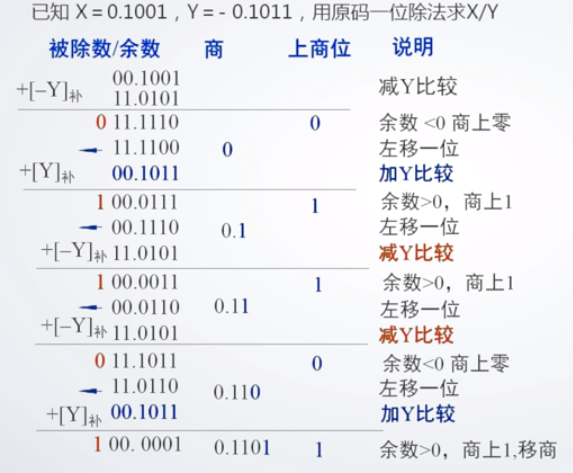
2.加减交替法（不恢复余数）：
不恢复余数法中，对Q<0得情况进行了修改，具体如下：
有被除数X除数Y。要计算X/Y。余数为Q。
符号位单独计算。取异或结果。
首先计算Q=X-Y，
如果Q<0则说明X<Y,商上0，余数左移一位，再加Y。
如果Q>0，则商上1,并对余数进行逻辑左移一位操作，再减Y。
之后每次用余数执行上述操作，即Q=Q±Y。加减由前一次的结果决定。
重复直到到达商所需要得位数即可。
6.浮点数加减运算：
对于浮点数的计算，需要保证参与运算的浮点数是规格化的。
由两个浮点数 A*2x和B*2y
做运算需要以下几个步骤
1.对阶：两个浮点数的阶数可能是不一样的即x和y的值不同，只有再x与y的阶数相同时才可以进行加减运算。于是需要对阶。
对阶原则是小阶码向大阶码看齐，即ΔE=x-y。将原来阶码小的数的尾数右移|ΔE|位,其阶码值加上|ΔE|,这种做法减小了精度。
2.计算：实现尾数的加(减)运算,对两个完成对阶后的浮点数执行求和(差)操作。
3.结果规格化：规格化处理,若得到的结果不满足规格化规则,就必须把它变成规格化的数。
4.舍入：即位数精度大于计算机存储范围，需要舍入，一般用0舍1入法，即可保存精度的最后一位的下一位，是0就直接舍弃，是1则向后加1。还有末尾恒1法，即可保存的末尾一位恒为1。
5.判结果的正确性,即检查阶码是否溢出:浮点数的溢出是以其阶码溢出表现出来的。在加减运算真正结束前,要检查是否产生了溢出,若阶码正常，加(减)运算正常结束；若阶码下溢,要置运算结果为浮点形式的机器零,若上溢,则置溢出标志。
