USACO2018(铂金组)
- [ 题解全部写完啦~ ]
[USACO18OPEN] Disruption P
题目描述:
你有一棵节点数为 \(n\),边数为 \(n-1\) 的树。然后你会给这棵树新增加 \(m\) 条边,对于每条边,有 \(u,v,w\) 分别表示边连接的两个节点分别为 \(u\) 和 \(v\),和一个边权 \(w\)。每次删掉一条原树边,然后如果要使原图依旧联通,则需要添加的额外边的边权最小为多少。
数据范围:
\(1\leq N\leq 5\times 10^4,1\leq M\leq 5\times 10^4\)
思路:
我们发现,如果去枚举到底删掉的是那一条边,则去计算最小加的边的边权是不太方便处理的。那我们不如换一种思路:对于每一条边,他能对那些边造成贡献。如图:
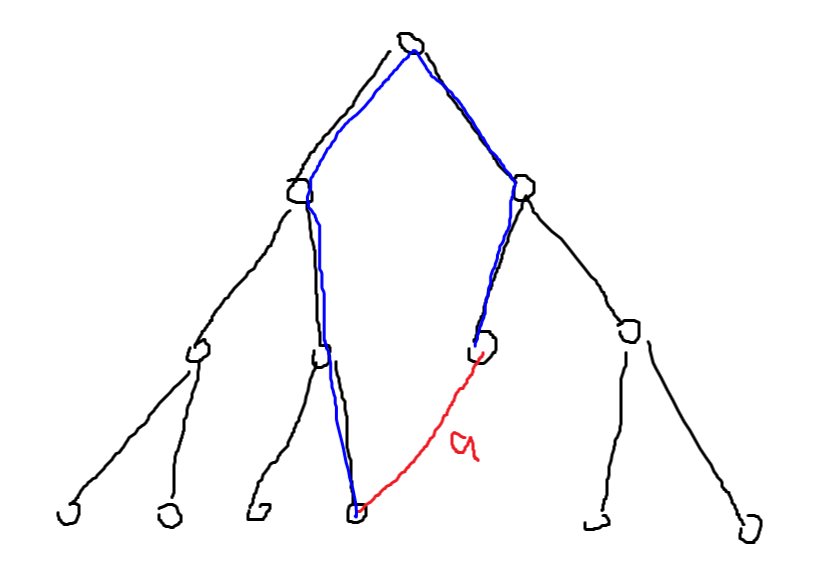
我们如果添加了一条边权为 \(a\) 的边,则可能造成贡献的边就应该为蓝色的路径所覆盖的边。因此问题转换为求区间最值的问题。显然可以用树剖+线段树维护。
但是,我们依旧认为这个方法过于的无脑,没有思维含量 其实是我不会
显然的,我们可以将所有的非树边全部按照边权排序,显然的,每次遍历到的最小的边所能造成影响的路径中的边全都应为这个非树边的边权。证明也是比较显然的。
对于这样的一个操作,我们可以使用并查集来维护。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
#define LOCAL
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=0x3f3f3f3f3f;
const int maxn=50005;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
void file(string s){freopen((s+".in").c_str(),"r",stdin);freopen((s+".out").c_str(),"w",stdout);return;}
int n,m;
vector<pair<int,int>>G[maxn];
struct Ds{
int fa[maxn];
int find(int x){
if(x!=fa[x])return fa[x]=find(fa[x]);
return fa[x];
}
}ds;
int fa[maxn][20];
int g[maxn],Id[maxn],dep[maxn];
void dfs(int u,int f){
dep[u]=dep[f]+1;
fa[u][0]=f;
g[u]=f;
for(auto k:G[u]){
int v=k.first,id=k.second;
if(v==f)continue;
Id[v]=id;
dfs(v,u);
}
}
int ans[maxn];
struct node{
int u,v,w;
bool operator<(const node&x)const{
return w<x.w;
}
}E[maxn];
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++)ds.fa[i]=i;
for(int i=1;i<n;i++){
int u,v;cin>>u>>v;
G[u].push_back({v,i});
G[v].push_back({u,i});
}
dfs(1,0);
for(int j=1;j<=18;j++){
for(int i=1;i<=n;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
}
for(int i=1;i<=m;i++){
cin>>E[i].u>>E[i].v>>E[i].w;
}
sort(E+1,E+m+1);
memset(ans,-1,sizeof(ans));
for(int i=1;i<=m;i++){
for(int a=ds.find(E[i].u),b=ds.find(E[i].v);a!=b;){
if(dep[a]<dep[b])swap(a,b);
ds.fa[a]=ds.fa[g[a]];
ans[Id[a]]=E[i].w;
a=ds.find(a),b=ds.find(b);
}
}
for(int i=1;i<n;i++)cout<<ans[i]<<endl;
return 0;
}
[USACO18DEC] Balance Beam P
题目描述:
有一个长度为 \(n\) 的序列,其中每个数为 \(a_i\)。以每个点 \(i\) 作为起点,你可以向左或者向右移动一次,概率分别为 \(\frac{1}{2}\),你到一个点之后也可以选择停止游戏,则你会获得 \(a_i\) 的收益;如果走出了 \(0\sim n-1\) 的范围,则会自动掉下去,并且不获得任何收益。对于每个 \(i\),求出以他为起点所能达到的最大的价值期望为多少。
数据范围:
\(1\leq N\leq 10^5\)
思路:
首先,我们不难想到一种贪心策略,即对于每个点,要么继续走,要么直接跳掉,所以此时我们令 \(E(x)\) 表示以 \(x\) 为起点所能达到的最大期望是多少,则我们可以列出转移方程:\(E(x)=\max(a_x,\frac{1}{2}(E(x-1)+E(x+1)))\)
其实仅仅观察这个式子,得不到什么有用的信息,则我们不妨从已知的条件入手:我们直到 \(a_x\) 的值。
所以考虑令点集 \(S=\{x|E(x)=a_x\}\),则对于其中的每两个相邻元素 \(p,q(p<q)\) ,所有 \(x\in[p,q]\) 都有 \(2\cdot E(x)=E(x-1)+E(x+1)\Rightarrow E(x)-E(x-1)=E(x+1)-E(x)\)。因此,\(E(x)=\frac{(q-x)\cdot a_p+(x-p)\cdot a_q}{q-p}\)
然后我就没有任何思路了。题解中都说停止点的图形是一个凸包,考虑反证:设存在一个停止点在凸包内,则这个点的停止期望小于移动期望,则显然这不是个停止点,与假设矛盾。
我们对停止点的定义进行一个补充:停止点就是对于一个点 \((x,a_x),(y,a_y)\) 之间的点 \((i,a_i)\),其中 \(i\in(x,y),a_i\gt f(x)\) 的点即为停止点。\(f(x)=\frac{a_y-a_x}{y-x}\cdot x+\frac{y\cdot a_x-x\cdot a_y}{y-x}\)
所有我们可以得到整体的思路:维护每个停止点 \((i,a_i)\) 的凸包,然后对于每个所要求的 \(E(x)\) 计算答案就可以了。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=0x3f3f3f3f3f;
const int maxn=1e5+5;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
int n;
int a[maxn];
int stk[maxn],top;
double slope(int x,int y){
return 1.0*(a[x]-a[y])/(x-y);
}
int ans[maxn];
signed main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i],a[i]*=100000;
for(int i=0;i<=n+1;i++){
while(top>1&&slope(stk[top-1],stk[top])<slope(stk[top-1],i))top--;
stk[++top]=i;
}
int pos=1;
for(int i=1;i<=n;i++){
while(stk[pos+1]<i)pos++;
ans[i]=slope(stk[pos],stk[pos+1])*(i-stk[pos])+a[stk[pos]];
cout<<ans[i]<<endl;
}
return 0;
}
[USACO18DEC] Sort It Out P
题目描述:
将选出一个集合 \(S\),对于 \(x\in S\),将 \(x\) 放到对应的第 \(x\) 个位置,问能否取出第 \(k\) 小的集合,使得操作完后原序列有序。
数据范围:
\(1\leq N\leq 10^5,1\leq K\leq 10^{18}\)
思路:
发现一个比较显然的事情,所有不在集合中的元素都应该在一开始就是有序的,即求第 \(k\) 大的最长上升子序列。
然后思考一下这个问题该怎么处理?首先肯定要处理出以每个 \(i\) 为开头的所有的最长上升子序列的长度和个数。
具体来说,考虑使用树状数组优化的方式,对于每个 \(f_i\),都可以从 \(f_1\sim f_{i-1}\) 之间转移。
求完了以上的信息,我们就可以考虑怎么弄出第 \(k\) 大的最长上升子序列了。首先我们开一个vector存所有长度为 \(x\) 的最长上升子序列的所有起始点。可以用试填法来处理。具体来说,从大往小枚举LIS的长度 \(i\),然后从大往小枚举下标,使得第 \(k\) 大的LIS在以这个下标为开头的后续长度为 \(i\) 的LIS中,这样我们就确定了一位,然后对于每一位,都像这样的方式去填。
其实本身有点类似于字典序第 \(k\) 小/大的排列
最后不要忘记取补集。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=1e18;
const int maxn=1e5+5;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
int n,k;
int a[maxn],b[maxn],lis[maxn],vis[maxn];
vector<int>G[maxn];
struct node{
int mx,cnt;
inline friend void operator += (node &a, const node &b) {
if (a.mx < b.mx) a.mx = b.mx, a.cnt = b.cnt;
else if (a.mx == b.mx) a.cnt = min(inf, a.cnt + b.cnt);
}
}tr[maxn];
int lowbit(int x){return x&-x;}
void add(int x,node k){
while(x){
tr[x]+=k;
x-=lowbit(x);
}
return ;
}
node query(int x){
node res={0,1};
while(x<=n){
res+=tr[x];
x+=lowbit(x);
}
return res;
}
signed main(){
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>a[i],b[a[i]]=i;
for(int i=n;i>=1;i--){
node res=query(b[i]+1);
res.mx++;
G[res.mx].push_back(i);
lis[i]=res.cnt;
add(b[i],res);
}
int m=query(1).mx;
int pos=-1;
for(int i=m;i>=1;i--){
for(int x:G[i]){
if(b[x]<pos)continue;
if(k<=lis[x]){
pos=b[x];
vis[x]=1;
break;
}
else k-=lis[x];
}
}
cout<<n-m<<endl;
for(int i=1;i<=n;i++){
if(!vis[i])cout<<i<<endl;
}
return 0;
}
[USACO18DEC] The Cow Gathering P
题目描述:
给你一颗节点数为 \(n\) 的树,其中每个点从叶子节点开始删,其中有 \(m\) 个限制,对于每个限制 \((a_i,b_i)\),则 \(a_i\) 必须要在 \(b_i\) 之前被删去。问每个点能否作为最终未被删去的点。
数据范围:
\(1\leq N,M\leq 10^5\)
思路:
这个题目我们可以考虑分类讨论一下:
- \(u\) 为 \(v\) 的祖先:令 \(u\) 的儿子节点中与 \(v\) 有祖先关系的点为 \(x\),则整棵树出去 \(x\) 的子树,全部打上标记
- \(v\) 为 \(u\) 的祖先:\(v\) 的子树全部打上标记
最后判断一下是否存在环就可以了 (不是很理解为什么这么处理)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=0x3f3f3f3f3f;
const int maxn=1e5+5;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
int n,m;
vector<int>G[maxn],E[maxn];
int dep[maxn],fa[maxn][20];
int L[maxn],R[maxn],idx,rnk[maxn];
void dfs(int u,int f){
L[u]=++idx;
rnk[idx]=u;
dep[u]=dep[fa[u][0]=f]+1;
for(int v:G[u]){
if(v==f)continue;
dfs(v,u);
}
R[u]=idx;
}
int jump(int u,int v){
for(int i=18;i>=0;i--){
if(dep[fa[v][i]]>dep[u])v=fa[v][i];
}
return v;
}
int ind[maxn],s[maxn],ans[maxn];
struct Ds{
int fa[maxn];
int find(int x){
if(x!=fa[x])return fa[x]=find(fa[x]);
return fa[x];
}
}ds;
struct Edge{
int u,v;
}e[maxn];
int vis[maxn];
bool check(){
queue<int>Q;
for(int i=1;i<=n;i++)if(ind[i]<2)Q.push(i),vis[i]=1;
while(!Q.empty()){
int u=Q.front();
Q.pop();
for(int v:G[u]){
ind[v]--;
if(!vis[v]&&ind[v]<2)Q.push(v),vis[v]=1;
}
for(int v:E[u]){
ind[v]--;
if(!vis[v]&&ind[v]<2)Q.push(v),vis[v]=1;
}
}
for(int i=1;i<=n;i++)if(!vis[i])return 0;
return 1;
}
signed main(){
cin>>n>>m;
for(int i=1;i<n;i++){
int u,v;cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
ind[u]++,ind[v]++;
}
for(int i=1;i<=n;i++)ds.fa[i]=i;
dfs(1,0);
for(int j=1;j<=18;j++){
for(int i=1;i<=n;i++){
fa[i][j]=fa[fa[i][j-1]][j-1];
}
}
for(int i=1;i<=m;i++){
int u,v;cin>>u>>v;
e[i]={u,v};
E[u].push_back(v);
ind[v]++;
if(L[u]<=L[v]&&R[u]>=R[v]){
int t=jump(u,v);
s[1]++,s[L[t]]--;
s[R[t]+1]++,s[n+1]--;
}
else{
s[L[u]]++;
s[R[u]+1]--;
}
}
if(!check()){
for(int i=1;i<=n;i++)cout<<0<<endl;
return 0;
}
for(int i=1;i<=n;i++){
s[i]+=s[i-1];
if(s[i]==0)ans[rnk[i]]=1;
}
for(int i=1;i<=n;i++)cout<<ans[i]<<endl;
return 0;
}
[USACO18JAN] Lifeguards P
题目描述:
给定 \(n\) 个半开半闭区间 \([l_i,r_i)\),求去除其中的 \(k\) 个后剩下的区间的并集最多可以覆盖多少个整数。
数据范围:
\(1\le n\le 10^5,1\le k\le \min(n,100),0\le l_i\le r_i\le 10^9\),保证 \(r_i\) 互不相同。
思路:
事实上这个题目直接暴力就可以过了:令 \(dp_{i,j}\) 表示前 \(i\) 个区间中,删掉 \(j\) 个后的区间最大长度,并且 限制第 \(i\) 个必须选
可以比较容易列出转移方程:\(dp_{i,j}=\min(dp_{k,j-len(i,k)}+R_i-\max(L_i,R_k+1))\)
点击查看代码
#include<bits/stdc++.h>
// #define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=0x3f3f3f3f;
const int maxn=1e5+5;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
int n,k;
struct node{
int l,r;
bool friend operator<(const node &a,const node &b){
if(a.r==b.r)return a.l>b.l;
return a.r<b.r;
}
}a[maxn],b[maxn];
int mn[maxn],cnt,dp[maxn][105];
signed main(){
re(n),re(k);
for(int i=1;i<=n;i++)re(a[i].l),a[i].l++,re(a[i].r);
sort(a+1,a+n+1);
for(int i=1;i<=n+1;i++)mn[i]=inf;
for(int i=n;i>=1;i--){
mn[i]=min(mn[i+1],a[i].l);
}
for(int i=1;i<=n;i++){
if(a[i].l>=mn[i+1])continue;
b[++cnt]=a[i];
}
k=max(0,k-(n-cnt));
n=cnt;
memset(dp,-inf,sizeof(dp));
dp[0][0]=0;
int ans=-inf;
// cout<<n<<" "<<k<<endl;
for(int i=1;i<=n;i++){
for(int j=0;j<=min(k,i-1);j++){
for(int l=0;l<=j;l++){
dp[i][j]=max(dp[i][j],dp[i-l-1][j-l]+b[i].r-max(b[i].l,b[i-l-1].r+1)+1);
}
}
ans=max(ans,dp[i][max(0,k-(cnt-i))]);
}
wt(ans),pt('\n');
return 0;
}
具体的优化暂时不会……
[USACO18JAN] Sprinklers P
题目描述:
一共有 \(n\) 个点,一个为与 \((x,y)\) 的点会使得 \((i,j),i\in [0,x],j\in[0,y]\) 这些格子打上标记 \(1\),\((i,j),i\in[x,n-1],j\in[y,n-1]\) 这些格子打上标记 \(2\)。你需要求出有多少不同的矩形使得这个矩形内部存在两种标记。
输出一个数,表示矩形的方案数,对 \(10^9+7\) 取模。
数据范围:
\(1\leq N\leq 10^5\)
思路:
对于这样的一个题目,我们可以求出对于每行 \([0,f_i]\) 被打了标记 \(1\),\([g_i,n-1]\) 被打了标记 \(2\)。我们可以求出这个 \(f_i,g_i\)。然后令上界为 \(j\),下界为 \(i\),则这对 \((i,j)\) 能对答案造成的贡献为 \(\frac{(f_i-g_j)\cdot (f_i-g_j+1)}{2}\),所以整个答案就是 \(\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{i-1}[g_j\leq f_i]\frac{(f_i-g_j)\cdot (f_i-g_j+1)}{2}\)
然后我们拆开这个式子:
\(\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{i-1}[g_j\leq f_i]\frac{g_j^2-g_j\cdot(2\cdot f_i+1)+(f_i^2+f_i)}{2}\)
观察这个式子,我们可以使用三个树状数组分别维护:
a1: \(\sum\limits_{j=0}^{i-1}[g_j\leq f_i]g_j^2\)
a2: \(\sum\limits_{j=0}^{i-1}[g_j\leq f_i]g_j\)
a3: \(\sum\limits_{j=0}^{i-1}[g_j\leq f_i]\)
则原式可以转化为:\(\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{i-1}[g_j\leq f_i]\frac{a1-a2\cdot(2\cdot f_i+1)+a3\cdot(f_i^2+f_i)}{2}\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=0x3f3f3f3f3f;
const int maxn=1e5+5;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
int n;
int p[maxn];
struct BIT{
int tr[maxn];
int lowbit(int x){
return x&-x;
}
void add(int x,int k){
x++;
while(x<n){
tr[x]+=k;
x+=lowbit(x);
}
}
int query(int x){
x++;
int res=0;
while(x){
res+=tr[x];
x-=lowbit(x);
}
return res;
}
}a1,a2,a3;
int g[maxn],f[maxn];
signed main(){
cin>>n;
for(int i=0;i<n;i++){
int x,y;
cin>>x>>y;
p[x]=y;
}
for(int i=0,now=n-1;i<n;i++){
now=min(now,p[i]);
g[i]=now;
}
for(int i=n-1,now=0;i>=0;i--){
now=max(now,p[i]);
f[i]=now;
}
int ans=0;
int inv2=5e8+4;
for(int i=0;i<n;i++){
int res=0;
int x1=a1.query(f[i]),x2=a2.query(f[i]),x3=a3.query(f[i]);
res=(res+x1-x2*(2*f[i]%mod+1)+x3*(f[i]*f[i]%mod+f[i])%mod+mod)%mod;
res=(res*inv2)%mod;
ans=(ans+res)%mod;
a1.add(g[i],g[i]*g[i]);
a2.add(g[i],g[i]);
a3.add(g[i],1);
}
cout<<(ans+mod)%mod<<endl;
return 0;
}
[USACO18JAN] Cow at Large P
题目描述:
给你一棵 \(n\) 个节点的树,根为 \(1\)。其中每个叶子节点是一个出口,农民只能存在于叶子节点且每个出口都可以放一个农民,Bessie可以从一个节点开始作为起点走到叶子节点。对于每一时刻,Bessie和农民都可以移动到相邻的节点。如果某一时刻,他们两个相遇,则Bessie被抓住了。这个过程中,他们都直到互相的位置。
问对于每个节点 \(i\) 作为Bessie的起点,最少需要放多少个农民才能使其被抓住。
数据范围:
\(2\leq N\leq 7\times 10^4\)
思路:
首先我们容易发现一个性质:
如果对于一个节点,如果这个点到一个叶子节点(必定是其叶子节点)的距离小于他的深度大小,则我们只用一个子树中的叶子节点就可以了,否则就使用整个子树中的所有叶子节点,才能封住这个节点。
对于这个性质,其实也很好理解。其实就是问如果像把这个子树中的所有叶子节点全部封住,则只需要将一个农夫在Bessie走到这个节点之前到达这个节点,就可以直接封死。
所以我们尽量找只需要一个农夫且子树大小最大的子树个数,这个就是答案了。
对于这个东西,需要满足 \(dep_u>g_u \land dep_{fa_u}<g_u\) \(g_u\) 为 \(u\) 这个节点距离叶子节点最近的距离
然后我们考虑怎么计算这个东西。在思考这个问题的时候,我们不妨将这颗子树认为是以 \(u\) 为根的子树,其中 \(u\) 为Bessie的起点。然后我们仔细观察一下上面这个判定式子,最后求出来的那个节点的子树,其实其中的所有节点都是满足上述的判定条件的。等于整棵子树的值赋为 \(1\)。
然后我们要想办法构造出这样的权值和。
下面这个部分是一个重点中的重点!!!非常脑洞。
构造方式
首先观察一下这个东西,我们将点权转换为边权,如图:
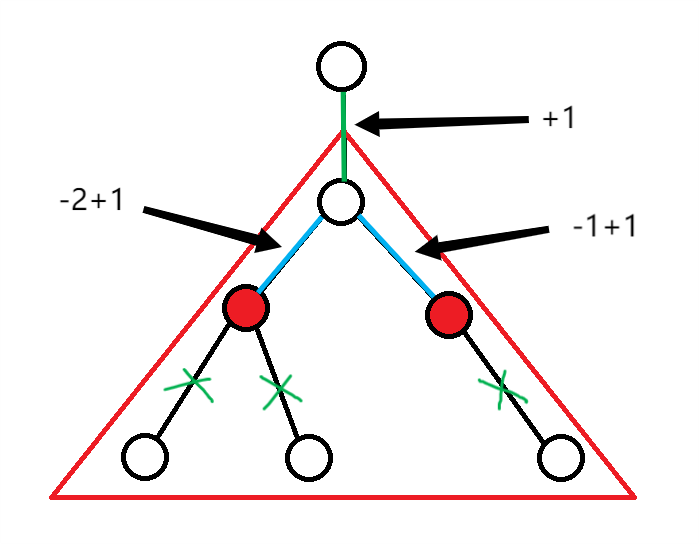
先解释一下这个图的意思:图中红色的三角形标记出来的子树就是满足条件的最大子树。我们首先可以考虑将点权转换为边权,则可以将整棵子树加 \(1\) 转换为绿色的边 \(+1\)。考虑一种通用的构造方式。
先看红色的节点,构造如下:\(w_u=-son_u+1\),\(son_u=deg_u-1\)。其实只需要自己手动模拟一下,就可以发现这个式子等同于一开始将所有叶子节点赋值为 \(1\),然后对于所有叶子节点的父亲节点,都需要减掉叶子节点的权值,然后 \(+1\)(可以理解为将这个点变为叶子节点)。这样做到最后,肯定是可以将绿色边 \(+1\) 的。
所以我们得到构造方式:\(\sum\limits_{i=1}^{n}[dis(u,i)>g_i](1-(deg_i-1))\)
其实对于这个式子,我们还有另外一种推导的方式:
\(\sum deg_u=2\times m-1\),\(m\) 表示节点个数。则这个式子可以推得 \(\sum (2-deg_i)=1\),所以也可以推的 \(\sum\limits_{i=1}^{n}[dis(u,i)>g_i](2-deg_i)\)
这道题目最重要的部分就完成了。对于实现中,有一个点需要注意一下:我们将原来的式子 \(dis(u,i)>g_i\) 转换为以 \(rt\) 为分治点,\(d_u+d_i>g_i\rightarrow d_u>g_i-d_i\)
直观来讲,可以直接用一个树状数组维护 \(g_i-d_i\),但其实好像直接暴力也没有问题……
复杂度 \(O(n\log n)\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mem(a) memset(a,0,sizeof(a))
#define set(a,b) memset(a,b,sizeof(a))
#define ls p<<1
#define rs p<<1|1
#define pb(x) push_back(x)
#define pt(x) putchar(x)
#define T int t;cin>>t;while(t--)
#define rand RAND
using namespace std;
char buf[1<<20],*p1,*p2;
#define gc()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
template<class Typ> Typ &re(Typ &x){char ch=gc(),sgn=0; x=0;for(;ch<'0'||ch>'9';ch=gc()) sgn|=ch=='-';for(;ch>='0'&&ch<='9';ch=gc()) x=x*10+(ch^48);return sgn&&(x=-x),x;}
template<class Typ> void wt(Typ x){if(x<0) putchar('-'),x=-x;if(x>9) wt(x/10);putchar(x%10^48);}
const int inf=0x3f3f3f3f3f;
const int maxn=7e4+5;
const int mod=1e9+7;
int seed = 19243;
unsigned rand(){return seed=(seed*48271ll)%2147483647;}
int n;
vector<int>G[maxn];
int dep[maxn],g[maxn],ind[maxn];
void dfs(int u,int f){
dep[u]=dep[f]+1;
g[u]=inf;
if(ind[u]==1)g[u]=0;
for(int v:G[u]){
if(v==f)continue;
dfs(v,u);
g[u]=min(g[u],g[v]+1);
}
return ;
}
void dfs1(int u,int f){
for(int v:G[u]){
if(v==f)continue;
g[v]=min(g[v],g[u]+1);
dfs1(v,u);
}
return ;
}
int sz[maxn],son[maxn],vis[maxn];
int rt,sum;
void getroot(int u,int f){
sz[u]=1;
son[u]=0;
for(int v:G[u]){
if(v==f||vis[v])continue;
getroot(v,u);
sz[u]+=sz[v];
son[u]=max(son[u],sz[v]);
}
son[u]=max(son[u],sum-sz[u]);
if(son[u]<son[rt])rt=u;
return ;
}
int ans[maxn];
struct node1{
int dg,deg;
bool operator<(const node1&a)const{
return dg<a.dg;
}
}q[maxn];
struct node2{
int id,dis;
bool operator<(const node2&a)const{
return dis<a.dis;
}
}p[maxn];
int d[maxn];
void getdis(int u,int f,int dep){
d[u]=dep;
for(int v:G[u]){
if(v==f||vis[v])continue;
getdis(v,u,dep+1);
}
}
int tot;
void add(int u,int f){
p[++tot]={u,d[u]};
q[tot]={g[u]-d[u],2-ind[u]};
for(int v:G[u]){
if(v==f||vis[v])continue;
add(v,u);
}
}
void calc(int u,int f,int op){
tot=0;
add(u,f);
sort(p+1,p+tot+1);
sort(q+1,q+tot+1);
int s=0,cur=0;
for(int i=1;i<=tot;i++){
while(cur<tot&&p[i].dis>=q[cur+1].dg){
cur++;
s+=q[cur].deg;
}
ans[p[i].id]+=op*s;
}
}
void solve(int u){
vis[u]=1;
getdis(u,0,0);
calc(u,0,1);
for(int v:G[u]){
if(vis[v])continue;
calc(v,u,-1);
sum=sz[v];
rt=0;
getroot(v,u);
solve(rt);
}
}
signed main(){
re(n);
for(int i=1;i<n;i++){
int u,v;re(u),re(v);
G[u].push_back(v);
G[v].push_back(u);
ind[u]++,ind[v]++;
}
dfs(1,0);
dfs1(1,0);
rt=0;
sum=son[rt]=n;
getroot(1,0);
solve(rt);
for(int i=1;i<=n;i++)if(ind[i]==1)ans[i]=1;
for(int i=1;i<=n;i++)wt(ans[i]),pt('\n');
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号