LeetCode - 70. 爬楼梯（人肉递归、动态规划）2

70 . 爬楼梯

题目：
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2

解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： 3
输出： 3

解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

递归的思维逻辑：
不要人肉进行递归
找最近重复子问题
数学归纳法的思维

递归模板：

public void recur(int level,int param){
    //terminator
    if(level > MAX_LEVEL){
        //process result
        return;
    }
    //process current logic
    process(level,param);
    //drill down
    recur(level:level+1,newParam);
    
    //restore current status
}

四要素：

1. recursion terminator 递归终结条件

2. process logic in current level 处理当前层逻辑

3. drill down 下探到下一层

4. reverse the current level status if needed 清理当前层

方法一： 人肉递归（超出时间限制）-- 不推荐
进行了很多重复的计算

class Solution {
    public int climbStairs(int n) {
        if(n==1 || n==2){
            return n;
        }else{
            return climbStairs(n-1) + climbStairs(n-2);
        }
    }
}

方法二： 避免重复的数，采用记忆递归的方法

public class Solution{
    public int climbStairs(int n){
        int memo[] = new int[n + 1];//记录爬到n级台阶的结果
        return climbStairsMemo(n,memo);
    }
    public int climbStairsMemo(int n,int memo[]){
        //如果爬到n级台阶时，n级台阶已经计算过了，则就直接返回n级台阶的计算结果
        //保证爬到每级台阶的结果只计算了一次
        if(memo[n] > 0){
            return memo[n];
        }
        if(n == 1){
            memo[n] = 1;
        }else if(n == 2){
            memo[n] = 2;
        }else{
            memo[n] = climbStairsMemo(n - 1, memo) + climbStairsMemo(n - 2,memo);
        }
        return memo[n];
    }
}

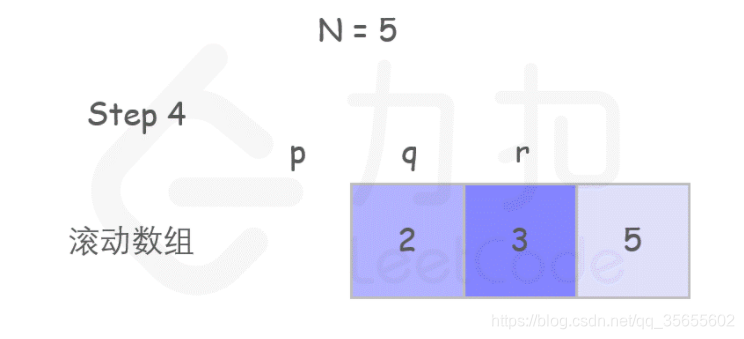
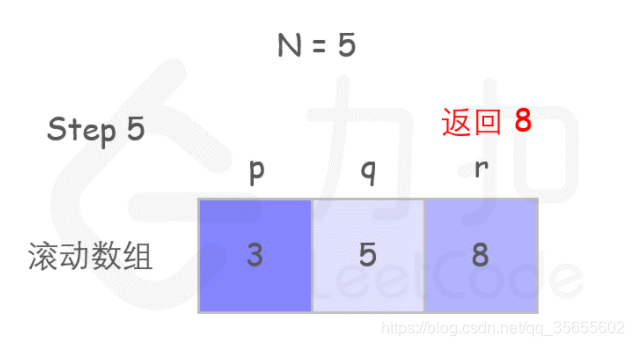
方法三：采用动态规划的方法：

只记住两个状态，用滚动数组的方式，

class Solution {
     public int climbStairs(int n) {
        int f1 = 1,f2 = 2,f3 = 3;
        if (n <= 2)
            return n;
        for (int i = 3; i < n + 1; i++) {
            f3 = f1 + f2;
            f1 = f2;
            f2 = f3;
        }
        return f3;
    }
}