【※重点※】剑指 Offer 32. 从上到下打印二叉树——队列、BFS（ 通常借助 队列 的先入先出特性来实现）

剑指 Offer 32 - I. 从上到下打印二叉树

题目描述——按层打印到一个数组中

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

  3
 / \
 9  20
   /  \
  15   7

返回：

[3,9,20,15,7]

题解（参考链接）

算法流程：

• 特例处理： 当树的根节点为空，则直接返回空列表 [] ；
• 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
• BFS 循环： 当队列 queue 为空时跳出；
  1. 出队： 队首元素出队，记为 node；
  2. 打印： 将 node.val 添加至列表 tmp 尾部；
  3. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
• 返回值： 返回打印结果列表 res 即可。

class Solution_32_1 {
    public int[] levelOrder(TreeNode root) {
        if (root == null) return new int[0];
        Queue<TreeNode> queue = new LinkedList<>(){{
                add(root);
            }
        };
        ArrayList<Integer> ans = new ArrayList<>();
        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            ans.add(node.val);
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        int[] res = new int[ans.size()];
        for (int i = 0; i < ans.size(); i++) {
            res[i] = ans.get(i);
        }
        return res;
    }
}

剑指 Offer 32 - II. 从上到下打印二叉树 II

题目描述

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: [3,9,20,null,null,15,7],

  3
 / \
 9  20
   /  \
  15   7

返回其层次遍历结果：

[
[3],
[9,20],
[15,7]
]

题解（参考链接）

• 特例处理： 当根节点为空，则返回空列表 [] ；
• 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
• BFS 循环： 当队列 queue 为空时跳出；

1. 新建一个临时列表 tmp ，用于存储当前层打印结果；
2. 当前层打印循环： 循环次数为当前层节点数（即队列 queue 长度）；
   1. 出队： 队首元素出队，记为 node；
   2. 打印： 将 node.val 添加至 tmp 尾部；
   3. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
3. 将当前层结果 tmp 添加入 res 。

• 返回值： 返回打印结果列表 res 即可。

class Solution_32_2 {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if (root != null) queue.add(root);
        while (!queue.isEmpty()){
            List<Integer> tmp = new ArrayList<>();
            for (int i = queue.size();i > 0; i--) {
                TreeNode node = queue.poll();
                tmp.add(root.val);
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

剑指 Offer 32 - III. 从上到下打印二叉树 III

题目描述

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

  3
 / \
 9  20
   /  \
  15   7

返回其层次遍历结果：

[
[3],
[20,9],
[15,7]
]

题解（参考链接）

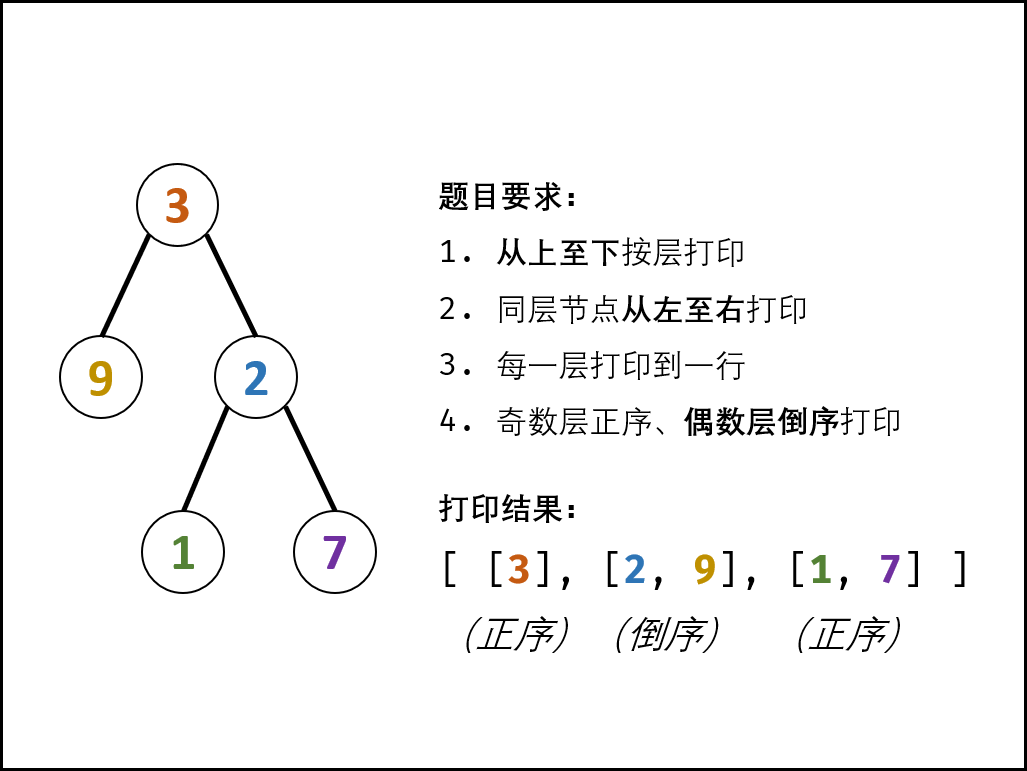
方法一：层序遍历 + 双端队列

利用双端队列的两端皆可添加元素的特性，设打印列表（双端队列） tmp ，并规定：

• 奇数层 则添加至 tmp 尾部 ，
• 偶数层 则添加至 tmp 头部 。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            LinkedList<Integer> tmp = new LinkedList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                if(res.size() % 2 == 0) tmp.addLast(node.val); // 偶数层 -> 队列头部
                else tmp.addFirst(node.val); // 奇数层 -> 队列尾部
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

方法二：层序遍历 + 双端队列（奇偶层逻辑分离）

• 通过将奇偶层逻辑拆分，可以消除冗余的判断。

• BFS 循环： 循环打印奇 / 偶数层，当 deque 为空时跳出；

  1. 打印奇数层： 从左向右 打印，先左后右 加入下层节点；
  2. 若 deque 为空，说明向下无偶数层，则跳出；
  3. 打印偶数层： 从右向左 打印，先右后左 加入下层节点；

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) deque.add(root);
        while(!deque.isEmpty()) {
            // 打印奇数层
            List<Integer> tmp = new ArrayList<>();
            for(int i = deque.size(); i > 0; i--) {
                // 从左向右打印
                TreeNode node = deque.removeFirst();
                tmp.add(node.val);
                // 先左后右加入下层节点
                if(node.left != null) deque.addLast(node.left);
                if(node.right != null) deque.addLast(node.right);
            }
            res.add(tmp);
            if(deque.isEmpty()) break; // 若为空则提前跳出
            // 打印偶数层
            tmp = new ArrayList<>();
            for(int i = deque.size(); i > 0; i--) {
                // 从右向左打印
                TreeNode node = deque.removeLast();
                tmp.add(node.val);
                // 先右后左加入下层节点
                if(node.right != null) deque.addFirst(node.right);
                if(node.left != null) deque.addFirst(node.left);
            }
            res.add(tmp);
        }
        return res;
    }
}

方法三：层序遍历 + 倒序（只用列表即可）

• 偶数层倒序： 若 res 的长度为 奇数 ，说明当前是偶数层，则对 tmp 执行 倒序 操作。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            if(res.size() % 2 == 1) Collections.reverse(tmp);
            res.add(tmp);
        }
        return res;
    }
}