剑指 Offer 33. 二叉搜索树的后序遍历序列
题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
题解 ( 参考链接 )
后序遍历定义: [ 左子树 | 右子树 | 根节点 ] ,即遍历顺序为 “左、右、根” 。
二叉搜索树定义: 左子树中所有节点的值 < 根节点的值;右子树中所有节点的值 > 根节点的值;其左、右子树也分别为二叉搜索树。
方法一:递归分治

public boolean verifyPostorder(int[] postorder) {
return recur(postorder,0, postorder.length - 1);
}
private boolean recur(int[] postorder, int left, int right) {
//如果left == right,就一个节点不需要判断了,如果left>right说明没有节点,不要判断,直接继续往下判断
if (left >= right) return true;
//因为数组中最后一个值postorder[right]是根节点,这里从左往右找出第一个比根节点大的值,
// 他后面的都是根节点的右节点(包含当前值,不包含最后一个值,因为最后一个数根节点),
// 他前面的都是根节点的左子节点
int mid = left;
while (postorder[mid] < postorder[right])
mid++;
int temp = mid;
while (postorder[mid] > postorder[right])
mid++;
//对左右子节点进行递归调用
return mid == right && recur(postorder,left,temp-1) && recur(postorder,temp,right-1);
}
方法二:辅助栈
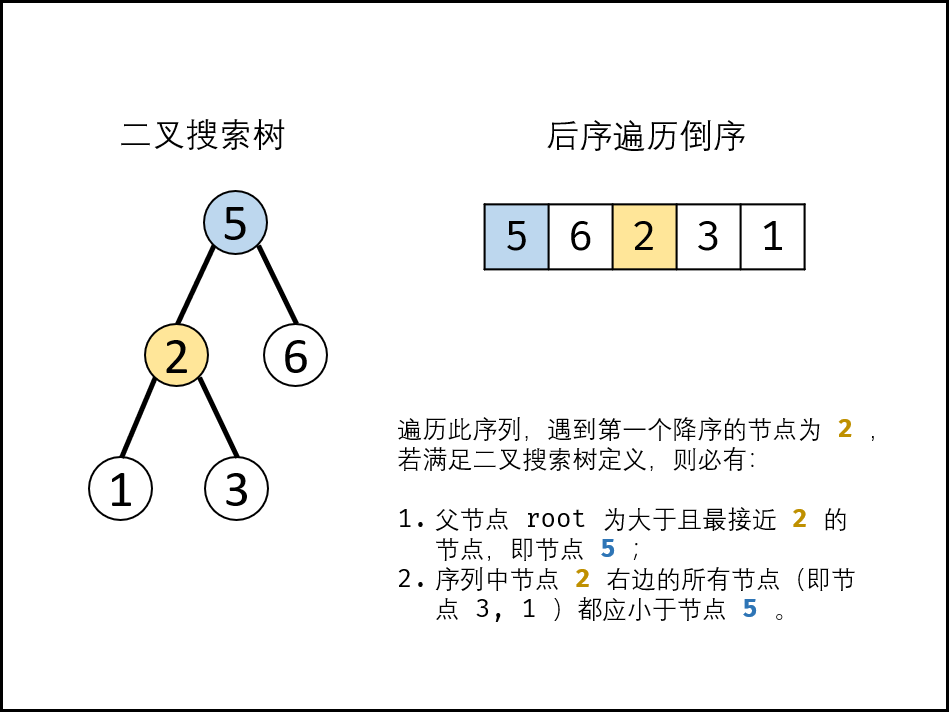

public boolean verifyPostorder(int[] postorder) {
Stack <Integer> stack = new Stack<>();
int root = Integer.MAX_VALUE;
for (int i = postorder.length - 1; i >= 0; i--) {
//如果前节点小于栈顶元素,说明栈顶元素和当前值构成倒叙
//说明当前节点是前面某个节点的左子节点,我们要找到他的父节点
if (postorder[i] > root) return false;
while (!stack.isEmpty() && stack.peek() > postorder[i]){
root = stack.pop();
}
stack.add(postorder[i]);
}
return true;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号