剑指 Offer 34. 二叉树中和为某一值的路径——回溯法，DFS

剑指 Offer 34. 二叉树中和为某一值的路径

题目描述

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 sum = 22，

          5
         / \
        4   8
       /   / \
      11  13  4
     /  \    / \
    7    2  5   1

返回:

[
[5,4,11,2],
[5,8,4,5]
]

题解（参考①、参考②）

可以采用减，或者加

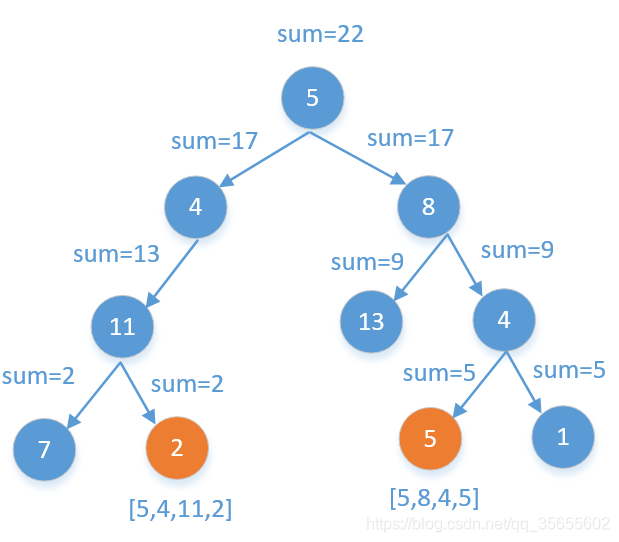
减：

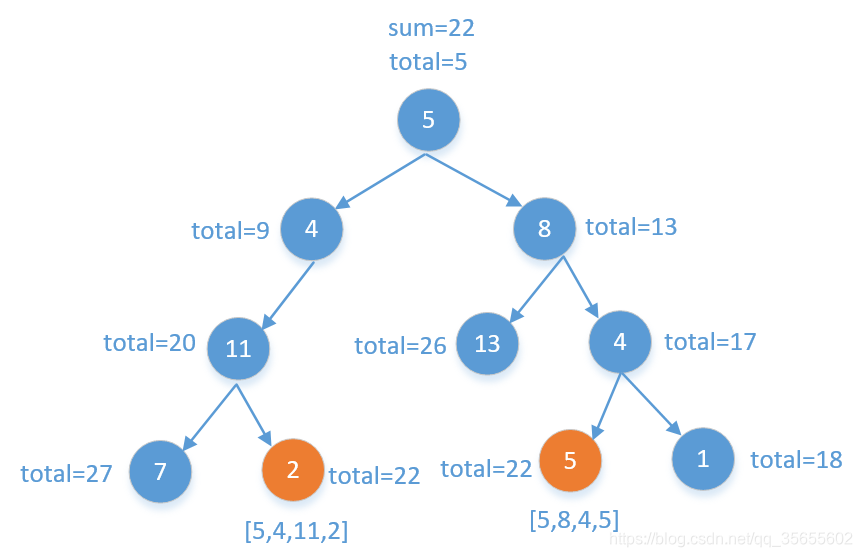
加：

方法一：递归 DFS

从根节点开始，用sum不断的减去遍历的每个节点，一直到叶子节点，看减去的叶子结点之前查看sum是否等于叶子节点。

注意：
记录路径时若直接执行 res.append(path) ，则是将 path 对象加入了 res ；后续 path 改变时， res 中的 path 对象也会随之改变。

正确做法：res.append(list(path)) ，相当于复制了一个 path 并加入到 res 。

public List<List<Integer>> pathSum(TreeNode root, int sum) {
    List<List<Integer>> result = new ArrayList<>();
    dfs(root, sum, new ArrayList<>(), result);
    return result;
}

public void dfs(TreeNode root, int sum, List<Integer> list,
                List<List<Integer>> result) {
    //如果节点为空直接返回
    if (root == null)
        return;
    //因为list是引用传递，为了防止递归的时候分支污染，我们要在每个路径
    //中都要新建一个subList
    List<Integer> subList = new ArrayList<>(list);
    //把当前节点值加入到subList中
    subList.add(new Integer(root.val));
    //如果到达叶子节点，就不能往下走了，直接return
    if (root.left == null && root.right == null) {
        //如果到达叶子节点，并且sum等于叶子节点的值，说明我们找到了一组，
        //要把它放到result中
        if (sum == root.val)
            result.add(subList);
        //到叶子节点之后直接返回，因为在往下就走不动了
        return;
    }
    //如果没到达叶子节点，就继续从他的左右两个子节点往下找，注意到
    //下一步的时候，sum值要减去当前节点的值
    dfs(root.left, sum - root.val, subList, result);
    dfs(root.right, sum - root.val, subList, result);
}

方法二：回溯，向下减

我们要理解递归的本质，当递归往下传递的时候他最后还是会往回走，
我们把这个值使用完之后还要把它给移除，这就是回溯

public List<List<Integer>> pathSum(TreeNode root, int sum) {
    List<List<Integer>> result = new ArrayList<>();
    dfs(root, sum, new ArrayList<>(), result);
    return result;
}

public void dfs(TreeNode root, int sum, List<Integer> list,
                List<List<Integer>> result) {
    //如果节点为空直接返回
    if (root == null)
        return;
    //把当前节点值加入到list中
    list.add(new Integer(root.val));
    //如果到达叶子节点，就不能往下走了，直接return
    if (root.left == null && root.right == null) {
        //如果到达叶子节点，并且sum等于叶子节点的值，说明我们找到了一组，
        //要把它放到result中
        if (sum == root.val)
            result.add(new ArrayList(list));
        //注意别忘了把最后加入的结点值给移除掉，因为下一步直接return了，
        //不会再走最后一行的remove了，所以这里在rerurn之前提前把最后
        //一个结点的值给remove掉。
        list.remove(list.size() - 1);
        //到叶子节点之后直接返回，因为在往下就走不动了
        return;
    }
    //如果没到达叶子节点，就继续从他的左右两个子节点往下找，注意到
    //下一步的时候，sum值要减去当前节点的值
    dfs(root.left, sum - root.val, list, result);
    dfs(root.right, sum - root.val, list, result);
    //我们要理解递归的本质，当递归往下传递的时候他最后还是会往回走，
    //我们把这个值使用完之后还要把它给移除，这就是回溯
    list.remove(list.size() - 1);
}

方法三：回溯，向下加

public List<List<Integer>> pathSum(TreeNode root, int sum) {
    List<List<Integer>> result = new ArrayList<>();
    dfs(root, sum, 0, new ArrayList<>(), result);
    return result;
}

public void dfs(TreeNode root, int sum, int toal, List<Integer> list,
                List<List<Integer>> result) {
    //如果节点为空直接返回
    if (root == null)
        return;
    //把当前节点值加入到list中
    list.add(new Integer(root.val));
    //没往下走一步就要计算走过的路径和
    toal += root.val;
    //如果到达叶子节点，就不能往下走了，直接return
    if (root.left == null && root.right == null) {
        //如果到达叶子节点，并且sum等于toal，说明我们找到了一组，
        //要把它放到result中
        if (sum == toal)
            result.add(new ArrayList(list));
        //注意别忘了把最后加入的结点值给移除掉，因为下一步直接return了，
        //不会再走最后一行的remove了，所以这里在rerurn之前提前把最后
        //一个结点的值给remove掉。
        list.remove(list.size() - 1);
        //到叶子节点之后直接返回，因为在往下就走不动了
        return;
    }
    //如果没到达叶子节点，就继续从他的左右两个子节点往下找
    dfs(root.left, sum, toal, list, result);
    dfs(root.right, sum, toal, list, result);
    //我们要理解递归的本质，当递归往下传递的时候他最后还是会往回走，
    //我们把这个值使用完之后还要把它给移除，这就是回溯
    list.remove(list.size() - 1);
}

我觉得上面的代码有点繁琐，不如：

向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.removeLast();

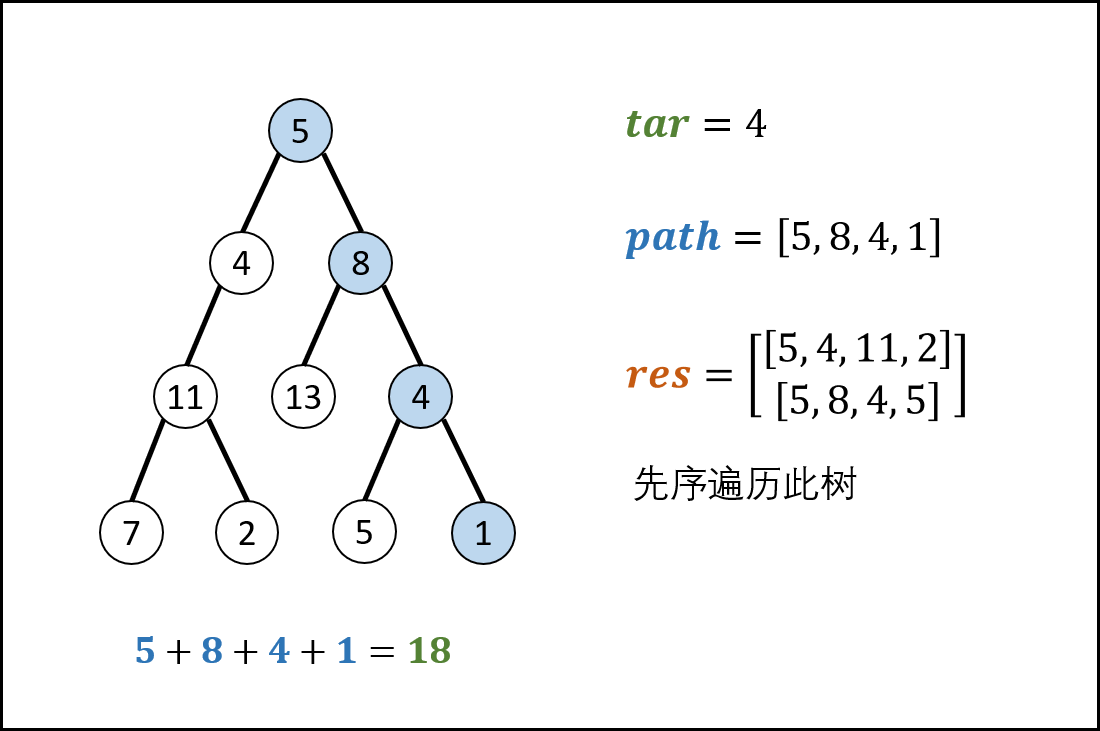
 LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        recur(root,sum);
        return res;

    }
    private void recur(TreeNode root, int tar) {
        if(root == null) return;
        path.add(root.val);
        tar -= root.val;
        if (tar == 0 && root.left == null && root.right == null){
            res.add(new LinkedList<>(path));
        }
        recur(root.left,tar);
        recur(root.right,tar);
        path.removeLast();
    }