海亮01/23图论计数专题

海亮01/23图论专题

个人题单

T1

P6657

题意

这是一道模板题。

有一个 \(n\times n\) 的棋盘，左下角为 \((1,1)\)，右上角为 \((n,n)\)，若一个棋子在点 \((x,y)\)，那么走一步只能走到 \((x+1,y)\) 或 \((x,y+1)\)。

现在有 \(m\) 个棋子，第 \(i\) 个棋子一开始放在 \((a_i,1)\)，最终要走到 \((b_i,n)\)。问有多少种方案，使得每个棋子都能从起点走到终点，且对于所有棋子，走过路径上的点互不相交。输出方案数 \(\bmod\ 998244353\) 的值。

两种方案不同当且仅当存在至少一个棋子所经过的点不同。

题解

关于 \(LGV\) 引理，这里不再证明（主要是我太菜了）

然后我们现在有

\[M= \left[ \begin{matrix} e(a_1,b_1)&e(a_1,b_2)&\cdots&e(a_1,b_m)\\ e(a_2,b_1)&e(a_2,b_2)&\cdots&e(a_2,b_m)\\ \vdots&\vdots&\ddots&\vdots\\ e(a_m,b_1)&e(a_m,b_2)&\cdots&e(a_m,b_m)\\ \end{matrix} \right]\\ \det(M)=\sum_{S:A\to B}(-1)^{t(\sigma(S))}\prod_{i=1}^nw(S_i) \]

然后发现，在这道题中，如果排列 \(\sigma(S)\) 有逆序对的话，那么显然无法保证路径不交这一限制，也就是说，题中要求的方案数正好等于右式。

然后有

\[e(a_i,b_j)= \begin{cases} {b_j+a_i+n-1\choose n-1}&b_j\ge a_i\\ 0&b_j<a_i \end{cases} \]

然后就没了。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool stmemory;
namespace Call_me_Eric{
inline int read(){
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 2e6 + 10, maxm = 1e2 + 10, mod = 998244353;
int fac[maxn], invfac[maxn];
int qpow(int x,int a){
    int res = 1;
    while(a){
        if(a & 1){res = res * x % mod;}
        x = x * x % mod;a >>= 1;
    }
    return res;
}
int C(int n,int m){return fac[n] * invfac[m] % mod * invfac[n - m] % mod;}
int n, m;
int a[maxm], b[maxm];
int arr[maxm][maxm];
int det(int n,int mod,int a[][maxm]){
    int res = 1, f = 1;
    for(int i = 1;i <= n;i++){
        int k = i;
        for(int j = i;j <= n;j++)if(a[j][i]){k = j;break;}
        if(!a[k][i])return 0;
        for(int j = k + 1;j <= n;j++)if(a[j][i] && a[j][i] < a[k][i])k = j;
        if(i != k){swap(a[i],a[k]);f = -f;}
        for(int j = i + 1;j <= n;j++){
            if(a[j][i] > a[i][i]){swap(a[j],a[i]);f = -f;}
            while(a[j][i]){
                int l = a[i][i] / a[j][i];
                for(int k = i;k <= n;k++)a[i][k] = (a[i][k] + (-l + mod) % mod * a[j][k] % mod) % mod;
                swap(a[j],a[i]);f = -f;
            }
        }
        res = res * a[i][i] % mod;
    }
    return (res * f + mod) % mod;
}
void main(){
    fac[0] = invfac[0] = 1;
    for(int i = 1;i < maxn;i++){fac[i] = fac[i - 1] * i % mod;}
    invfac[maxn - 1] = qpow(fac[maxn - 1],mod - 2);
    for(int i = maxn - 2;i;i--){invfac[i] = invfac[i + 1] * (i + 1) % mod;}
    auto solve = []()->int{
        n = read(); m = read();
        for(int i = 1;i <= m;i++){a[i] = read();b[i] = read();}
        for(int i = 1;i <= m;i++)
            for(int j = 1;j <= m;j++)
                arr[i][j] = ((b[j] >= a[i]) ? C(b[j] - a[i] + n - 1,n - 1) : 0);
        return det(m,mod,arr);
    };
    int T = read();
    while(T--){printf("%lld\n",solve());}
    return;
}
};
bool edmemory;
signed main(){
    auto stclock = clock();
    Call_me_Eric::main();
    auto edclock = clock();
    cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << " Mib cost.\n";
    cerr << (edclock - stclock) * 1.0 / CLOCKS_PER_SEC << " Sec cost.\n";
    return 0;
}

T3

P7736

题意

小 L 有一个有向图，图中的顶点可以分为 \(k\) 层，第 \(i\) 层有 \(n_i\) 个顶点，第 \(1\) 层与第 \(k\) 层顶点数相同，即 \(n_1 = n_k\)，且对于第 \(j\)（\(2 \leq j \leq k-1\)）层，\(n_1 \leq n_j \leq 2n_1\)。对于第 \(j\)（\(1 \leq j < k\)）层的顶点，以它们为起点的边只会连向第 \(j + 1\) 层的顶点。没有边连向第 \(1\) 层的顶点，第 \(k\) 层的顶点不会向其他顶点连边。

现在小 L 要从这个图中选出 \(n_1\) 条路径，每条路径以第 \(1\) 层顶点为起点，第 \(k\) 层顶点为终点，并要求图中的每个顶点至多出现在一条路径中。更具体地，把每一层顶点按照 \(1,2,\ldots,n_1\) 进行编号，则每条路径可以写为一个 \(k\) 元组 \((p_1,p_2,\ldots,p_k)\)，表示这条路径依次经过第 \(j\) 层的 \(p_j\)（\(1 \leq p_j \leq n_j\)）号顶点，并且第 \(j\)（\(1 \leq j < k\)）层的 \(p_j\) 号顶点有一条边连向第 \(j+1\) 层的第 \(p_{j+1}\) 号顶点。

小 L 把这些路径画在了纸上，发现它们会产生若干个交点。对于两条路径 \(P,Q\)，分别设它们在第 \(j\) 层与第 \(j+1\) 层之间的连边为 \((P_j,P_{j+1})\) 与 \((Q_j,Q_{j+1})\)，若，

\[(P_j-Q_j)\times(P_{j+1}-Q_{j+1})<0 \]

则称它们在第 \(j\) 层后产生了一个交点。两条路径的交点数为它们在第 \(1, 2,\ldots,k - 1\) 层后产生的交点总数。对于整个路径方案，它的交点数为两两不同路径间交点数之和。例如下图是一个 \(3\) 条路径，共 \(3\) 个交点的例子，其中红色点是交点。

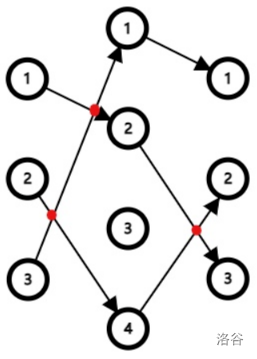
小 L 现在想知道有偶数个交点的路径方案数比有奇数个交点的路径方案数多多少个。两个路径方案被视为相同的，当且仅当它们的 \(n_1\) 条路径按第一层起点编号顺序写下的 \(k\) 元组能对应相同。由于最后的结果可能很大，请你输出它对 \(998244353\)（一个大质数）取模后的值。

题解

发现一个性质，就是路径交点个数只和始末位置有关，如果出现一对逆序对，那么就会出现一个奇数交点的路径。

然后发现这个性质之后，所求答案就是右式。

然后考虑左式的矩阵怎么求。

发现可以矩阵乘法维护，然后你就赢了。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool stmemory;
namespace Call_me_Eric{
inline int read(){
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 200 + 10, mod = 998244353;
struct Matrix{
    int n, m;
    int a[maxn][maxn];
    Matrix(int n = 0,int m = 0):n(n),m(m){for(int i = 1;i <= n;i++)for(int j = 1;j <= m;j++)a[i][j] = 0;}
    friend Matrix operator * (Matrix a,Matrix b){
        Matrix c = Matrix(a.n,b.m);
        for(int i = 1;i <= a.n;i++)
            for(int k = 1;k <= b.n;k++)
                for(int j = 1;j <= b.m;j++)
                    c.a[i][j] = (c.a[i][j] + (a.a[i][k] * b.a[k][j] % mod)) % mod;
        return c;
    }
}A,B;
int det(int n,int mod,int a[][maxn]){
    int res = 1, f = 1;
    for(int i = 1;i <= n;i++){
        int k = i;
        for(int j = i;j <= n;j++)if(a[j][i]){k = j;break;}
        if(!a[k][i])return 0;
        for(int j = k + 1;j <= n;j++)if(a[j][i] && a[j][i] < a[k][i])k = j;
        if(i != k){swap(a[i],a[k]);f = -f;}
        for(int j = i + 1;j <= n;j++){
            if(a[j][i] > a[i][i]){swap(a[j],a[i]);f = -f;}
            while(a[j][i]){
                int l = a[i][i] / a[j][i];
                for(int k = i;k <= n;k++)a[i][k] = (a[i][k] + (-l + mod) % mod * a[j][k] % mod) % mod;
                swap(a[j],a[i]);f = -f;
            }
        }
        res = res * a[i][i] % mod;
    }
    return (res * f + mod) % mod;
}

int k;
int n[maxn], m[maxn];
void solve(){
    k = read();
    for(int i = 1;i <= k;i++)n[i] = read();
    A = Matrix(n[1],n[1]);
    for(int i = 1;i <= n[1];i++)A.a[i][i] = 1;
    for(int i = 2;i <= k;i++)m[i] = read();
    for(int i = 2;i <= k;i++){
        B = Matrix(n[i - 1],n[i]);
        for(int j = 1;j <= m[i];j++){
            int u = read(), v = read();
            B.a[u][v] = 1;
        }
        A = A * B;
    }
    printf("%lld\n",det(n[1],mod,A.a));
}
void main(){
    int T = read();
    while(T--){solve();}
    return;
}
};
bool edmemory;
signed main(){
    auto stclock = clock();
    Call_me_Eric::main();
    auto edclock = clock();
    cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << " Mib cost.\n";
    cerr << (edclock - stclock) * 1.0 / CLOCKS_PER_SEC << " Sec cost.\n";
    return 0;
}

T12

CF156D

题意

给定一个 \(n\) 个点 \(m\) 条边的带标号无向图，它有 \(k\) 个连通块，求添加 \(k-1\) 条边使得整个图连通的方案数，答案对 \(p\) 取模。

题解

没学过 \(Prüfer\) 序列 的自行学习。

不太会严谨证明

我们发现，如果将 \(k\) 个连通块缩成一个点，那么剩下 \(k\) 个孤立点（有标号），然后问你完全图 \(K_k\) 生成树有多少棵。

这个显然就是 \(Cayley\) 公式，有 \(n^{k-2}\) 种。

但是不太对，因为你没有确定每条边连接的是连通块中哪一个具体的点。

考虑用 \(Prüfer\) 序列重构树的过程，对于每一个序列，每一个点都需要拎出来连边，而这个连边的方案显然有 \(siz_u\) 个（设 \(siz_u\) 是连通块 \(u\) 的大小），然后发现每个连边都互不影响，然后你就赢了：P

最终答案是 \(n^{k-2}\prod siz_{u}\)。

这里需要注意，如果原来给定的图就是一整个连通块，那么方案数显然是 \(1\)，不过有一个点的 \(p=1\)，所以一定不要 \(puts("1")\) 要 \(1\mod p\) 啊（

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool stmemory;
namespace Call_me_Eric{
inline int read(){
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 1e5 + 10;
int n, m, mod;
int qpow(int x,int a){
    int res = 1;
    while(a){
        if(a & 1)res = (1ll * res * x) % mod;
        x = 1ll * x * x % mod;a >>= 1;
    }
    return res;
}

int fa[maxn], siz[maxn];
int getf(int x){return fa[x] == x ? x : fa[x] = getf(fa[x]);}

void main(){
    n = read(); m = read(); mod = read();
    if(n == 1){printf("%lld\n",1ll % mod);return;}
    for(int i = 1;i <= n;i++)fa[i] = i;
    for(int i = 1;i <= m;i++){
        int u = read(), v = read();
        if(getf(u) != getf(v))fa[getf(u)] = getf(v);
    }
    for(int i = 1;i <= n;i++){siz[getf(i)]++;}
    int ans = 1, cnt = 0;
    for(int i = 1;i <= n;i++){if(siz[i]){ans = (ans * siz[i]) % mod;cnt++;}}
    if(cnt == 1){printf("%lld\n",1ll % mod);return;}
    printf("%lld\n",ans * qpow(n,cnt - 2) % mod);
    return;
}
};
bool edmemory;
signed main(){
    auto stclock = clock();
    Call_me_Eric::main();
    auto edclock = clock();
    cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << " Mib cost.\n";
    cerr << (edclock - stclock) * 1.0 / CLOCKS_PER_SEC << " Sec cost.\n";
    return 0;
}

T14

ARC106_F

题意

有 \(N\) 个点，每个点有 \(a_i\) 个孔，每次可以选择两个不同点，连接两个未被连接过的孔，有多少中方案使得最后形成一棵树。

题解

显然的一个结论是，除了根节点，每个节点都有个父节点，那么我们对每一个点，钦定一个特殊孔连向父亲的非特殊孔，那么这个选择方案就有 \(\prod_{i=1}^nd_i\)。

然后发现第 \(i\) 次选择非特殊点（去连向特殊点）的方案是 \(\sum_{j=1}^nd_j-n-i\) 的（刚开始选完了 \(n\) 个特殊点，然后在前 \(i-1\) 次中选完了 \(i\) 个非特殊点）

然后最终答案就是 \(\prod_{i=1}^nd_i \times \prod_{j=0}^{n-3}(\sum_{i=1}^nd_i-n-j)\)

为什么后面式子是 \(0\sim n-3\)？考虑类似 \(Prüfer\) 重构树的过程，最终只会连接 \(n-2\) 次。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool stmemory;
namespace Call_me_Eric{
inline int read(){
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 2e5 + 10, mod = 998244353;
int n;
void main(){
    n = read();int sum = 0, prod = 1;
    for(int i = 1;i <= n;i++){
        int t = read();
        sum += t;prod *= t; prod %= mod;
        sum = (sum >= mod) ? (sum - mod) : sum;
    }
    for(int i = 0;i <= n - 3;i++){prod = (prod * (sum - n - i)) % mod;}
    printf("%lld\n",prod);
    return;
}
};
bool edmemory;
signed main(){
    auto stclock = clock();
    Call_me_Eric::main();
    auto edclock = clock();
    cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << " Mib cost.\n";
    cerr << (edclock - stclock) * 1.0 / CLOCKS_PER_SEC << " Sec cost.\n";
    return 0;
}