CF1207

CF1207

CF1207A

link

CF1207A题意

在你的餐厅里有两种汉堡：牛肉汉堡和鸡肉汉堡。每个牛肉汉堡需要$2$片面包和$1$片牛肉，一个鸡肉汉堡需要$2$片面包和$1$个鸡排。

一个牛肉汉堡卖$h$元，一个鸡肉汉堡卖$c$元。

你有$b$片面包，$p$片牛肉和$f$块鸡排。求最大收益。

CF1207A题解

可以发现肯定尽可能发现选单价多的问题。

CF1207A代码

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int x = 0, f  = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch= getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
int b, p, f, h, c;
signed main(){
int T = read();
while(T--){
    b = read(); p = read(); f = read();
    h = read(); c = read();
    if(h < c){swap(h, c);swap(p, f);}
    int a = min(b / 2, p);
    int ans = a * h;
    ans += min((b - 2 * a) / 2,f) * c;
    printf("%d\n",ans);
}
    return 0;
}

CF1207B

link

CF1207B题意

给定一个 $n\times m(n,m\le 50)$ 的01目标矩阵和一个全是0的原始矩阵，每次可以对点 $(i,j)(i<n,j<m)$ 进行操作，使得原始矩阵中 $(i,j),(i+1,j),(i,j+1),(i+1,j+1)$ 的位置改成1。不要求尽可能少操作，只要求给出一个解法即可。

CF1207B题解

不要求最少操作，那就能操作就操作呗：）
具体而言，如果目标矩阵中$(i,j),(i+1,j),(i,j+1),(i+1,j+1)$ 都是1，那就操作 $(i,j)$
最后判一下能不能行就好了。

CF1207B代码

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int x = 0, f  = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch= getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 51;
int a[maxn][maxn],b[maxn][maxn],n, m;
bool book[maxn][maxn];
vector<pair<int,int> > vec;
signed main(){
    n = read(); m = read();
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            a[i][j] = read();
    for(int i = 0;i <= n;i++)a[i][0] = 1;
    for(int i = 0;i <= m;i++)a[0][i] = 1;
    for(int i = 2;i <= n;i++)
        for(int j = 2;j <= m;j++)
            if(a[i][j] && a[i - 1][j] && a[i][j - 1] && a[i - 1][j - 1]){
                book[i][j] = 1;
            }
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            if(book[i][j]){
                b[i][j] = b[i - 1][j] = b[i][j - 1] = b[i - 1][j - 1] = 1;
            }
    int ans = 0;
    for(int i = 1;i <= n && ans != -1;i++)
        for(int j = 1;j <= m;j++){
            if(a[i][j] != b[i][j]){ans = -1;break;}
            if(book[i][j]){ans++;vec.push_back(make_pair(i,j));}
        }
    if(ans != -1){
        printf("%d\n",ans);
        for(auto i : vec){printf("%d %d\n",i.first - 1,i.second - 1);}
    }
    else puts("-1");
    return 0;
}

CF1207C

link

CF1207C题意

你需要在城市里修建管道和支柱，管道和支柱的单位长度的价格分别为$a,b$

给你一个长度为$n$的$01$序列，其中$1$表示这里需要通车，$0$表示这里不需要通车，高度为$2$的地方才可以通车(保证序列的头尾不需要通车)

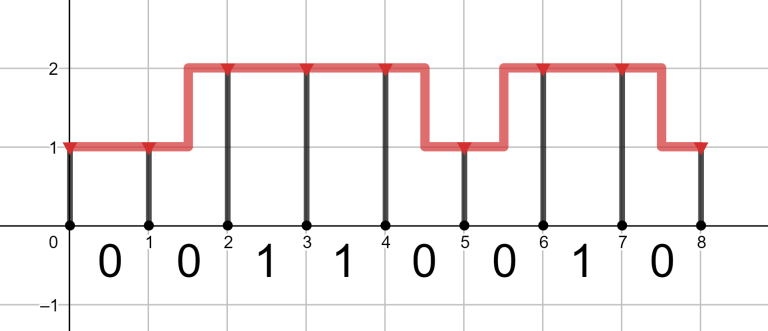
如图，红色表示管道，黑色表示支柱，我们可以在一段单位区间建立一条S形线条，每个S形可以表示为该段由三部分组成：$0.5$个单位的水平管道+$1$个单位的垂直管道+$0.5$个单位的水平管道

每一段的单位区间左右都有支柱支撑，支柱的高度等于管道端点的高度

你需要保证所有通车的地方高度为$2$的同时，建管道和支柱的费用总和最小

CF1207C题解

简单DP那你还调半天？！
设 $f_{i,0/1}$ 表示第 $i$ 个支柱是高度为1还是2的最小值。
于是就有

• $f_{i,0}=\min (f_{i-1,0}+a+b,f_{i-1,1}+2a+b)$
• $f_{i,1}=\min (f_{i-1,0}+2a+2b,f_{i-1,1}+a+2b)$

然后注意题意，题中说的是i~i+1的高度，不是第i个支柱的高度，故\

• $f_{i,0}=INF(s_i==1||s_{i+1}==1)$

没了。

CF1207C代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
    int x = 0, f  = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch= getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 2e5 + 10;
int f[maxn][2];
int n, a, b;
char ch[maxn];
signed main(){
int T = read();
while(T--){
    memset(f,0x3f,sizeof f);
    n = read(); a = read(); b = read();
    scanf("%s",ch + 1);f[0][0] = b;
    for(int i = 1;i <= n;i++){
        f[i][0] = min(f[i - 1][0] + a + b,f[i - 1][1] + 2LL * a + b);
        f[i][1] = min(f[i - 1][0] + 2LL * a + 2LL * b,f[i - 1][1] + a + 2LL * b);
        if(ch[i] == '1' || ch[i + 1] == '1')f[i][0] = 0x3f3f3f3f3f3f3f3f;
    }
    // for(int i = 1;i <= n;i++){printf("i=%lld:%lld %lld\n",i,f[i][0],f[i][1]);}
    printf("%lld\n",f[n][0]);
}
    return 0;
}

CF1207D

link

CF1207D题意

给 $n(n\le 3\times 10^5)$ 个二元组 $(a_i,b_i)$， 问排列后第一元或第二元不按照非严格升序排列的排列方式有多少种。答案对998244353取模。

CF1207D题解

简单容斥+计数
经典trick：第一元或第二元不按照非严格升序排列 $\iff$ 总排列数-第一元按照非严格升序排列-第二元按照非严格升序排列+第一元第二元同时按照非严格升序排列。
然后注意一下可能加一次998244353不能为正，需要加好几次。吃我一次提交（
没了。

CF1207D代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
    int x = 0, f  = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch= getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 3e5 + 10, mod = 998244353;
int n;
struct node{
    int first, second;
    node(int f = 0,int s = 0):first(f),second(s){}
}a[maxn];
int typ, pw[maxn];
bool cmp(node a,node b){
    if(typ == 1){return a.first < b.first;}
    if(typ == 2){return a.second < b.second;}
    if(typ == 3){return a.first != b.first ? a.first < b.first : a.second < b.second;}
}

int calc(int type){
    typ = type; sort(a + 1,a + 1 + n,cmp);
    int len = 1, times = 1;
    // printf("type = %lld\n",type);
    // for(int i = 1;i <= n;i++)printf("%lld %lld\n",a[i].first,a[i].second);
    for(int i = 1;i <= n && times != 0;i++){
        switch(type){
            case 1:{
                if(a[i].first == a[i - 1].first){len++;}
                else {times = times * pw[len] % mod;len = 1;}
                break;
            }
            case 2:{
                if(a[i].second == a[i - 1].second){len++;}
                else {times = times * pw[len] % mod;len = 1;}
                break;
            }
            case 3:{
                if(a[i].second < a[i - 1].second){times = 0;}
                if(a[i].first == a[i - 1].first && a[i].second == a[i - 1].second){len++;}
                else {times = times * pw[len] % mod;len = 1;}
                break;
            }
            default:break;
        }
    }
    return times * pw[len] % mod;
}

signed main(){
    n = read(); int u, v, ans = 1;pw[0] = 1;
    for(int i = 1;i <= n;i++){
        pw[i] = pw[i - 1] * i % mod;
        u = read(); v = read();
        a[i] = node(u, v);
    }
    int tmp = (pw[n] - calc(1) - calc(2) + calc(3) + mod) % mod;
    while(tmp < 0)tmp += mod;
    printf("%lld\n",tmp);
    return 0;
}

CF1207E

link

CF1207E题意

交互题
现在有一个在 $[0,2^{14}-1]$ 的数字 $x$，只让你问两次，每次你需要恰好给出 100 个不能重复的数字。
交互库会随机选一个数 $a_i$，返回你 $x\oplus a_i$ 的值。

CF1207E题解

这啥啊
不难想到 $a_i\oplus x\oplus b_j\oplus x=a_i\oplus b_j$
现在想构造两个序列，使得对于一个异或值 $tmp$，最多只有一组 $(i,j)$ 满足 $tmp=a_i\oplus b_j$
不难想到，让 $a\in [1,100]$，$b\in [1<<7,100<<7]$，这样一定不会有重复。
然后就没了。

CF1207E代码

#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int x = 0, f  = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch= getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int mod = (1 << 14);
vector<int> vec1, vec2;
bool book[mod];
signed main(){
    for(int i = 1;i <= 100;i++)vec1.push_back(i);
    for(int i = 1;i <= 100;i++)vec2.push_back(i << 7);
    cout << "?"; for(int i : vec1){cout << ' ' << i;}cout << endl;
    int tmp1;cin >> tmp1;
    cout << "?"; for(int i : vec2){cout << ' ' << i;}cout << endl;
    int tmp2;cin >> tmp2;
    int x = 0, y = 0;bool flag = 0;
    for(int i : vec1){
        if(flag)break;
        for(int j : vec2)
            if((i ^ j) == (tmp1 ^ tmp2)){
                flag = 1;x = i,y = j;break;
            }
    }
    cout << "! " << (tmp1 ^ x) << endl;
    return 0;
}

CF1207F

link

CF1207F题意

给你一个长度为 $500000$ 的序列，初值为 $0$ ，你要完成 $q$ 次操作，操作有如下两种：

1. 1 x y : 将下标为 $x$ 的位置的值加上 $y$
2. 2 x y : 询问所有下标模 $x$ 的结果为 $y$ 的位置的值之和

CF1207F题解

根号分治模板题。
先想两种暴力方式。

1. 每次强行在原序列加，询问时每次暴力跳 $x$，时间复杂度 $O(\frac{n^2}{x})$，修改时直接改 $a_x$，时间复杂度 $O(1)$，空间复杂度 $O(n)$
2. 预处理 $f_{i,j}$ 表示下标模 $i$ 是 $j$ 的位置的值之和。每次询问时直接输出预处理结果即可，时间复杂度 $O(1)$，修改时枚举1~x的模数，暴力修改即可，时间复杂度 $O(nx)$，空间复杂度 $O(nx)$

不难发现，这两个暴力可以捏在一起，然后设置一个阈值 $lim$，当 $x>lim$ 时跑第一个暴力，$x\le lim$ 时跑第二个暴力。
当$lim=\sqrt{n}$时时空复杂度都是最优的 $O(n\sqrt{n})$

CF1207F代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1; ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + ch - '0'; ch = getchar();}
    return x * f;
}
const int maxn = 500000 + 10, maxm = 1e3 + 10;
int n, q, len;
int a[maxn];
int dp[maxm][maxm];
signed main(){
    int opt, x, y;
    n = 5e5; q = read(); len = sqrt(n);
    while(q--){
        opt = read(); x = read(); y = read();
        if(opt == 1){
            a[x] += y;
            for(long long i = 1;i <= len;i++){
                dp[i][x % i] += y;
            }
        }
        else{
            if(x <= len)printf("%lld\n",dp[x][y % x]);
            else{
                int ans = 0;
                for(long long i = y % x;i <= n;i += x)ans += a[i];
                printf("%lld\n",ans);
            }
        }
    }
    return 0;
}