海亮01/18图论专题
海亮01/18图论专题
T1
题意
有一个 \(n\times m\) 的棋盘,被 \(1\times2\) 的骨牌覆盖,保证 \(2\mid nm\)。
现在你需要执行以下操作:
- 移去恰好一张骨牌。
- 将一张骨牌沿着其长边进行移动。你可以进行这一步任意次。
- 你需要保证在任意时刻,每张骨牌的位置与其初始位置至少有一个公共格子。
求你可以得到的所有可能的局面的数量。
两种局面不同,当且仅当某个位置在其中一者中被骨牌覆盖,而在另一者中没有。
\(nm\le2\times10^5\)。
输入格式为:输入一张大小为 \(n\times m\) 的矩阵,位置 \((i,j)\) 为 L/R/U/D 表示其被一张骨牌的 左/右/上/下 端覆盖。
题解
首先先来想一个问题,如果在一个位置 \((x,y)\) 有一个空位,怎么刻画这个空位的移动?
发现如果一个空格子站在 \((i,j)\) 能够向下移动,当且仅当 \((i+1,j),(i+2,j)\)(其他方向同理)上面的是同一块骨牌。
然后可以按照这个连接有向边。
我们来考虑下这样连接完之后是什么图。
首先,每个点最多只有一个入度(这个显然,考虑一张骨牌的一头,显然只可能从向另一头方向走两格的位置连过来)
那么这个东西已经是一棵外向基环森林了。
可是真的有环吗?
我们尝试用骨牌拼成一个环。(拿画图做的非常丑陋)
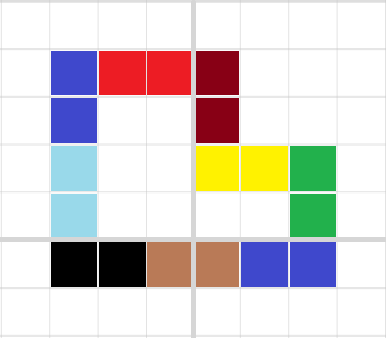
根据pick's theorem,显然有 \(A=i+\frac{b}{2}-1\)。
然后由于组成的图形上下(左右)一一对应,并且每一个骨牌占两格格子,那么显然有 \(4|b\),也就是说,\(2|\frac{b}{2}\)
然后就发现这里面的 \(i\) 一定是奇数,不符合题意。
然后就发现这道题的一个非常厉害的性质:这是个外向森林。
而且将整张图黑白染色之后,发现黑点到不了白点,但是一个骨牌占一个黑点一个白点,也就是说,移除一张骨牌能够得到的局面相当于黑点能到达的位置 \(\times\) 白点能到达的位置。
显然发现每个点能够到达的位置数量就是自己的子树大小。
那么移除一个骨牌能够产生的最终状态(贡献)就是骨牌所在两个点的子树大小的乘积。
upd 2024/1/19:这里有个小问题,移除一个骨牌的最终状态不一定是子树大小乘积,具体原因在下面说(感谢来自 @Maverik 提出不同的思路)
不过这里出现一个小问题,我们设 \(((x,y),(u,v))\) 表示最后剩下的两个空位置(钦定第一个是黑点 \(a\),第二个是白点 \(b\)),那么相同的 \(((x,y),(u,v))\) 显然只能统计一次。
不过有的时候会重复统计,怎么办?
发现我们在计算子树大小的时候,顺便标一下每个点的 \(dfs\) 序,这个骨牌的贡献就是使得 \(x\in[dfn_a,dfn_a+siz_a-1],y\in[dfn_b,dfn_b+siz_b-1],(x,y)\) 的最终局面存在。
提示到这了,思路就明显了,直接上扫描线即可。
注意空间开大点啊(
upd 2024/1/19:
在这里说明为什么移除一个骨牌贡献不一定是子树大小乘积。
这里给出一张图:
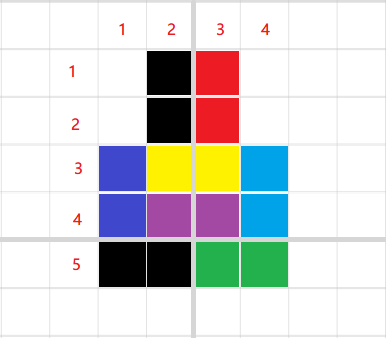
考虑移除绿色的骨牌,如果按照上面的连边方式,那么显然有 \((5,4)\to(3,4)\to(3,2)\to(1,2)\) 和 \((5,3)\to(5,1)\to(3,1)\to(3,3)\to(1,3)\)。
但是这里发现一个问题,就是当两个空格分别在 \((3,1)\) 和 \((3,4)\) 的时候,你发现这两个空格不能同时出现在 \((3,2),(3,3)\)(图中黄骨牌),也就是说,黑白格子影响到了对方的路径。
但是为什么仍然是对的呢?
因为出现这种情况当且仅当两个空格子想要到同一个骨牌的两个位置但是互相卡住了。
但是我们可以直接移除这个骨牌,然后这两个空格子就出现在想去的两个位置了。
也就是说,虽然一张骨牌能够提供的最终状态不一定是子树乘积,但是缺的状态能够在其他的骨牌的子树乘积中补全,于是就对了。
翻了一遍题解发现好像没有人说这件事情。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
bool stmemory;
const int maxn = 4e5 + 10;
int n, m;
inline int getid(int i,int j){return (i - 1) * m + j;}
vector<int> mp[maxn];
//L=0,U=1,R=2,D=3
inline int optid(char ch){if(ch == 'R')return 0;if(ch == 'D')return 1;if(ch == 'L')return 2;if(ch == 'U')return 3;}
const int dx[4] = { 0,-1, 0, 1};
const int dy[4] = {-1, 0, 1, 0};
char ch[maxn];
vector<int> edg[maxn];
int fa[maxn];
int dfn[maxn], idx, low[maxn];
void dfs(int u){dfn[u] = ++idx;for(int v : edg[u])dfs(v);low[u] = idx;}
struct scanline{
int x, y, opt;
scanline(int x = 0,int y = 0,int opt = 0
):x(x),y(y),opt(opt){}
};
vector<scanline> vec[maxn];
struct Segment_Tree{
struct node{
int l, r;int minn, cnt;//minn 是区间tag决定是否用儿子更新,cnt是有面积的位置总数。
node(int l = 0,int r = 0,int minn = 0,int cnt = 0):l(l),r(r),minn(minn),cnt(cnt){}
}d[maxn << 2];
void pushup(int p){
if(d[p].minn){d[p].cnt = d[p].r - d[p].l + 1;}
else d[p].cnt = d[p << 1].cnt + d[p << 1 | 1].cnt;
}
void build(int l,int r,int p){
d[p] = node(l, r);if(l == r)return;
int mid = l + r >> 1;
build(l,mid,p << 1);build(mid + 1,r,p << 1 | 1);
pushup(p);
}
void update(int l,int r,int s,int t,int p,int upd){
if(s <= l && r <= t){d[p].minn += upd;pushup(p);return;}
int mid = l + r >> 1;
if(s <= mid)update(l,mid,s,t,p << 1,upd);
if(mid < t)update(mid + 1,r,s,t,p << 1 | 1,upd);
pushup(p);
}
int query(){return d[1].cnt;}
}tree;
bool edmemory;
signed main(){
cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << "Mib cost.\n";
n = read();m = read();
for(int i = 1;i <= n;i++){
mp[i].resize(m + 1); scanf("%s",ch + 1);
for(int j = 1;j <= m;j++) mp[i][j] = optid(ch[j]);
}
// puts("11111111");
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
for(int k = 0;k < 4;k++){
int nx = i + dx[k] * 2, ny = j + dy[k] * 2;
if(nx < 1 || nx > n || ny < 1 || ny > m)continue;
if(mp[nx][ny] != (k + 2) % 4)continue;
edg[getid(i, j)].push_back(getid(nx,ny));
fa[getid(nx,ny)] = getid(i, j);
}
}
}
// puts("22232322222");
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if(!dfn[getid(i,j)]){
int u = getid(i, j);
while(fa[u])u = fa[u];
dfs(u);
}
}
}
// puts("3333343333343");
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if((i + j) & 1){
int nx = dx[mp[i][j]] + i, ny = dy[mp[i][j]] + j;
int xl = dfn[getid(i, j)], xr = low[getid(i, j)];
int yu = dfn[getid(nx,ny)],yd = low[getid(nx,ny)];
// printf("(%d, %d), (%d, %d)\n",i,j,nx,ny);
// printf("%d %d %d %d\n",xl,xr,yu,yd);
vec[xl ].push_back(scanline(yu,yd,1));
vec[xr + 1].push_back(scanline(yu,yd,-1));
}
}
}
// puts("4444444444");
int ans = 0;tree.build(1,idx,1);
for(int i = 1;i <= idx;i++){
for(auto v : vec[i]){tree.update(1,idx,v.x,v.y,1,v.opt);}
ans += tree.query();
}
printf("%lld\n",ans);
return 0;
}
T2
题意
给定01字符串 \(s\),现在你能进行若干次操作,对于每一次操作:
- 选择字符串 \(s\) 的连续的一段子串,要求这段子串必须包含同样数量的字符
0与1. - 把该子串的所有字符转换,即所有字符
0换为1,字符1换为0. - 把选中的子串反转.
比如设字符串 \(s=\) 00111011.
我们可以选择前六个字符 001110 进行操作,这个操作合法是因为 0 和 1 的数量一致,选择 00111,0 等都是不合法的.
然后把这六个字符转换,变为 110001.
最后反转整个字串,变为 100011.
最终经过一次操作,我们就可以得到字符串 10001111.现在给定字符串 \(s\),求经过若干次操作后字典序最小的字符串.
\(T\) 组询问.保证 \(1\leq\sum len(s)\leq5\times10^5.\)
题解
有一个很显然的trick,让 \(1\gets 1,0\gets -1\),那么做一个前缀和,发现当 \(s_{l-1}=s_r\) 的时候可以翻转区间 \([l,r]\)。
然后发现原题的操作在前缀和上变成了反转(没有转换)区间前缀和。
然后发现,如果在记录前缀和的过程中(设 \(x=s_{i-1}\),\(a_i=y\)),连边 \(x\to x+y\),然后就发现,刚刚的翻转变成了选择哪条边走。
然后发现一条欧拉路径就是最终答案。
然后就可以贪心了,每次尽可能向下走,除非需要向上走且向下走回不来才向上走。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 1e6 + 10;
char ch[maxn];
int e[maxn][2];//0 \leftarrow,1\rightarrow
void solve(){
scanf("%s",ch + 1);int n = strlen(ch + 1);
int x = 0;
for(int i = 1;i <= n;i++){
if(ch[i] == '0'){e[n + 1 + x][0]++;x--;}
else{e[n + 1 + x][1]++;x++;}
}
x = 0;int cnt = 0;
while(cnt < n){
if((e[n + 1 + x][0] && e[n + 1 + x - 1][1]) || (!e[n + x + 1][1])){
ch[++cnt] = '0';e[n + 1 + x][0]--;x--;
}
else{
ch[++cnt] = '1';e[n + 1 + x][1]--;x++;
}
}
puts(ch + 1);
}
signed main(){
int T = read();
while(T--){solve();}
return 0;
}
T5
题意
给定 \(n\) 与 \(k\),问是否能将 \(n\) 分为若干个 \(k\) 的因数(\(1\) 除外)之和,每个因数都可以被选多次。
\(n\leq 10^{18}\),\(k\leq 10^{15}\),最多 \(50\) 种不同的 \(k\)。
一共 \(t\) 组询问,\(t\leq 10^4\)。
题解
首先发现一个性质,如果 \(n\) 能够用 \(k\) 的因数拼起来,那就一定能够用质因数拼起来,证明显然。
然后只有 \(50\) 个不同的 \(k\),显然将相同 \(k\) 的询问放到一起,这里只讨论一对 \((n,k)\) 的计算方式。
然后对 \(k\) 分类讨论:
- \(k=1\):直接就寄了不用看了。
- \(k\) 只有一个质因数(\(k\) 是质数):判定下 \(k|n\) 成不成立即可。
- \(k\) 有两个质因数:设两个质因数分别是 \(x,y\),然后发现如果 \(n\) 能够表示出来,那么一定有 \(a\times x+b\times y=n\),发现这个就是 \(exgcd\),算一下即可。
- \(k\) 有三个以上质因数:
- 首先,\(k\) 的最小的质因数一定不超过 \(\sqrt[3]{k}=10^5\)。
- 其次,\(k\) 最多有 \(13\) 个质因数。
- 然后,这个可以参照P3403 跳楼机的思想跑同余最短路。
- 然后最后判定下 \(n\ge dis_{n\mod p}\) 即可。
然后你就做完了。
至于 \(pollard-rho\),我最慢的点跑了 \(1.3s\),时限 \(5s\) 你怕啥?
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
bool stmemory;
namespace Call_me_Eric{
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 1e5 + 10, maxq = 3.2e7 + 10,INF = 0x3f3f3f3f3f3f3f3f;
bitset<maxq> bookprime;
vector<int> prime;
unordered_map<int,vector<pair<int,int> > > mp;
bool ans[maxn];
int exgcd(int &x,int &y,int a,int b){
if(b == 0){x = 1;y = 0;return a;}
int t = exgcd(y,x,b,a % b);
y -= x * (a / b);return t;
}
void init(){
for(int i = 2;i < maxq;i++){
if(!bookprime[i])prime.push_back(i);
for(int j : prime){
if(i * j >= maxq)break;
bookprime[i * j] = 1;if(i % j == 0)break;
}
}
}
int dis[maxn];queue<int> que;bool book[maxn];
void solve(int k,vector<pair<int,int> > vec){
// printf("%lld\n",k);
if(k == 1)return;
vector<int> fac;
for(int i : prime){
if(i > k)break;
if(k % i == 0){
fac.push_back(i);
while(k % i == 0)k /= i;
}
}
if(k > 1)fac.push_back(k);
if(fac.size() == 1){
for(auto i : vec)ans[i.second] = (i.first % fac.back() == 0);
return;
}
if(fac.size() == 2){
int x, y, g = exgcd(x,y,fac[0],fac[1]), s = fac[1] / g;
for(auto i : vec){
int n = i.first, id = i.second;
if(n % g != 0)ans[id] = 0;
int u = ((__int128_t)x * (n / g) % s + s) % s;
ans[id] = (n >= fac[0] * u);
}
return;
}
int p = fac[0];
fill(dis + 1,dis + 1 + p,INF);dis[0] = 0;
for(int i : fac){
if(i != p){
int c = __gcd(i, p);
for(int d = 0;d < c;d++){
int tim = 0;
for(int u = d,nxt = (u + i) % p;tim <= 2;u = nxt,nxt = (u + i) % p){
tim += (u == d);dis[nxt] = min(dis[nxt],dis[u] + i);
}
}
}
}
for(auto i : vec){
int n = i.first, id = i.second;
ans[id] = n >= dis[n % p];
}
}
void main(){
init();int T = read();
for(int i = 1;i <= T;i++){
int n = read(), k = read();
mp[k].push_back(make_pair(n, i));
}
for(auto u : mp){solve(u.first,u.second);}
for(int i = 1;i <= T;i++)puts(ans[i] ? "YES" : "NO");
}
};
bool edmemory;
signed main(){
auto begintime = clock();
Call_me_Eric::main();
auto endtime = clock();
cerr << 1.0 * (endtime - begintime) / CLOCKS_PER_SEC << " sec cost.\n";
cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << "Mib cost.\n";
return 0;
}
T6
题意
给定一张 \(n\) 个点的竞赛图。边分为粉色和绿色。粉色的边有 \(m\) 条,你已经知道了它们的方向。而绿色的边你不知道方向。
每次询问,你可以获得一条绿色的边的方向。
你需要在 \(2n\) 次询问内,找到一个点 \(u\),使得对于每个点 \(v\),都有一条 \(u\to v\) 的路径,使得路径上每条边同色。需要注意的是路径只能通过粉边和你已经询问的绿边。
交互库是自适应的。
\(n, m \leq 10^5\)。
题解
考虑没有粉色边怎么做。
设集合 \(A\) 中的点表示可能为答案的点。
然后思路就很显然了,每次随便找集合 \(A\) 的两个点 \(u,v\),问下 \(u\to v\) 是不是对的。
然后每次删除被指向的那个点。
然后最后剩下的那个点一定是对的。
但是现在有粉色边捣乱怎么办?
先将只有粉色边的图跑个强连通分量,然后每个分量里面找一个点做代表放进 \(A\) 集合里,剩下的点显然可以被这个点用粉边到达。
然后在剩下的点里面用刚刚的算法。
但是有个问题,就是每个分量里面所有点都可以作为代表对吧,但是如果对于同一个分量里面的点 \(u,v\),如果 \(u\) 不行,不代表 \(v\) 不行,可是刚刚的方法直接判了 \(v\) 死刑,咋办?
我们通过保留一些边使得原图变成一个 \(DAG\),然后每次删除一个点 \(v\) 之后,都删除他连出去的边,如果有的点入度变成 \(0\),就加入这个点即可。
然后就没了。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 1e5 + 10;
int n, m;
vector<int> edg[maxn], to[maxn];
int vis[maxn], bel[maxn], deg[maxn];
void tarjan(int u){
vis[u] = 1;bel[u] = 1;
for(int v : edg[u]){
if(!bel[v]){to[u].push_back(v);deg[v]++;}
if(!vis[v])tarjan(v);
}
bel[u] = 0;
}
vector<int> A;
signed main(){
n = read(); m = read();
for(int i = 1;i <= m;i++){int u = read(), v = read();edg[u].push_back(v);}
for(int i = 1;i <= n;i++)if(!vis[i])tarjan(i);
for(int i = 1;i <= n;i++)if(!deg[i])A.push_back(i);
while(A.size() > 1){
int u = A.back();A.pop_back();
int v = A.back();A.pop_back();
printf("? %d %d\n",u, v);fflush(stdout);
if(!read()){swap(u, v);}A.push_back(u);
for(int w : to[v]){if(!--deg[w])A.push_back(w);}
}
printf("! %d\n",A.back());fflush(stdout);
return 0;
}
T9
题意
给定一张 \(n\) 个点的竞赛图,定义一次操作为选取一个顶点 \(v\) 并翻转所有以 \(v\) 为顶点的边的方向。
请你判断是否存在一种操作方案使得操作完成后,这个图是强连通的。如果存在,求出最小的操作次数,以及使得操作次数达到最小的操作方案数。其中,方案数对 \(998244353\) 取模。
Note: 有向图 \(G\) 是强连通的,当且仅当对于任意有序顶点对 \((x,y)\),\(G\) 中存在一条从 \(x\) 到 \(y\) 的路径。
保证 \(3\le n\le 2000\)。
题解
有三个非常nb的结论(但是我不会证,怎么回事呢?)
- 当 \(n\ge 4\) 时,\(n\) 阶强连通竞赛图有 \(n-1\) 阶强连通竞赛子图。
- 当 \(n\ge 7\) 时,只需要翻转一个节点就可以让它强连通。
- 由兰道定理推得,在将出度序列排序之后,如果 \(\forall i\in[1,n),\sum_{j=1}^id_j\neq {k\choose2}\),那么这个竞赛图就是强连通的。
但是不会证(
那么思路就显然了,当 \(n\le 6\) 的时候直接暴力枚举翻转情况,否则枚举翻转哪个即可。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2000 + 10;
bool e[maxn][maxn];
int n;
char ch[maxn];
int buc[maxn];
int d[maxn], deg[maxn];
void rev(int x,int y){deg[x] -= e[x][y];e[x][y] ^= 1;deg[x] += e[x][y];}
void upd(int x){for(int i = 1;i <= n;i++)rev(x,i),rev(i,x);}
bool check(){
for(int i = 0;i < n;i++)buc[i] = 0;
for(int i = 1;i <= n;i++)buc[deg[i]]++;
int pos = 0, sum = 0;
for(int i = 0;i < n;i++)
while(buc[i]){d[++pos] = i;buc[i]--;}
for(int i = 1;i < n;i++){sum += d[i]; if(sum == i * (i - 1) / 2)return false;}
return true;
}
int ans1,ans2;
void solve1(){
ans1 = 114514;
for(int sta = 0;sta < (1 << n);sta++){
int tot = 0;
for(int i = 1;i <= n;i++)
if(sta & (1 << (i - 1))){
upd(i);tot++;
}
if(tot <= ans1 && check()){
if(tot == ans1){ans2++;}
else {ans1 = tot;ans2 = 1;}
}
for(int i = 1;i <= n;i++)
if(sta & (1 << (i - 1)))
upd(i);
}
for(int i = 1;i <= ans1;i++)ans2 *= i;
}
void solve2(){
ans1 = 1;
for(int i = 1;i <= n;i++){
upd(i);ans2 += check();upd(i);
}
}
void print(){
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
printf("%d%c",e[i][j]," \n"[j == n]);
for(int i = 1;i <= n;i++){
printf("deg[%d] = %d\n",i,deg[i]);
}
puts("");
}
signed main(){
n = read();
for(int i = 1;i <= n;i++){
scanf("%s",ch + 1);
for(int j = 1;j <= n;j++){
e[i][j] = (ch[j] == '1');
deg[i] += e[i][j];
}
}
if(check()){puts("0 1");return 0;}
if(n <= 6){solve1();}else solve2();
if(ans1 == 114514)puts("-1");
else printf("%d %d\n",ans1,ans2);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号