海亮01/11网络流专题
海亮01/11网络流杂题
T1
题意
一共有 \(n\) 个飞行员,其中有 \(m\) 个外籍飞行员和 \((n - m)\) 个英国飞行员,外籍飞行员从 \(1\) 到 \(m\) 编号,英国飞行员从 \(m + 1\) 到 \(n\) 编号。 对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
题解
二分图最大匹配不做解释。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f =1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2e2 + 10,maxm = maxn * maxn, INF = 0x3f3f3f3f;
int n, m;
int head[maxn], tot = 1;
struct edge{
int to, nexte, cap, flow;
edge(int to = 0,int ne = 0,int ca = 0,int fl = 0):to(to),nexte(ne),cap(ca),flow(fl){}
}e[maxm * 2];
void add(int u,int v,int cap){e[++tot] = edge(v,head[u],cap);head[u] = tot;}
void addd(int u,int v,int cap){add(u,v,cap);add(v, u, 0);}
int dep[maxn], cur[maxn];
int dfs(int u,int flow,int T){
// printf("%lld\n",u);
if(u == T)return flow;
int rest = 0, tmp = 0;
for(int i = cur[u];i && flow;i = e[i].nexte){
cur[u] = i; int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && (dep[v] == dep[u] + 1)){
tmp = dfs(v,min(flow,e[i].cap - e[i].flow),T);
if(tmp == 0)dep[v] = INF;
e[i].flow += tmp; e[i ^ 1].flow -= tmp;
flow -= tmp;rest += tmp;
if(!flow)return rest;
}
}
return rest;
}
bool bfs(int S,int T){
queue<int> que;
for(int i = 1;i <= n + 3;i++){dep[i] = INF;cur[i] = 0;}
que.push(S);dep[S] = 1; cur[S] = head[S];
while(!que.empty()){
int u = que.front(); que.pop();
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && dep[v] == INF){
que.push(v);
cur[v] = head[v];
dep[v] = dep[u] + 1;
if(v == T)return 1;
}
}
}
return 0;
}
int Dinic(int S,int T){
int mxflow = 0;
while(bfs(S,T)){mxflow += dfs(S,INF,T);}
return mxflow;
}
signed main(){
m = read(); n = read();int u, v;
int S = n + 1, T = n + 2;
for(int i = 1;i <= m;i++)addd(S,i,1);
for(int i = m + 1;i <= n;i++)addd(i,T,1);
while((u = read()),(v = read()),(u != -1 && v != -1)){addd(u, v, 1);}
int ans = Dinic(S,T);
printf("%d\n",ans);
for(u = 1;u <= m;u++){
v = 0;
for(int i = head[u];i;i = e[i].nexte){
if(e[i].cap == e[i].flow && e[i].cap == 1){
v = e[i].to;break;
}
}
if(v)printf("%d %d\n",u,v);
}
return 0;
}
T2
题意
有一个 \(m\) 行 \(n\) 列的方格图,每个方格中都有一个正整数。现要从方格中取数,使任意两个数所在方格没有公共边,且取出的数的总和最大,请求出最大的和。
题解
黑白染色之后,问题转化为最小割。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x = 0, f =1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 1e4 + 10,maxm = 1e6 + 10, INF = 0x3f3f3f3f3f3f3f3f;
int n, m;
int head[maxn], tot = 1;
struct edge{
int to, nexte, cap, flow;
edge(int to = 0,int ne = 0,int ca = 0,int fl = 0):to(to),nexte(ne),cap(ca),flow(fl){}
}e[maxm * 2];
void add(int u,int v,int cap){e[++tot] = edge(v,head[u],cap);head[u] = tot;}
void addd(int u,int v,int cap){add(u,v,cap);add(v, u, 0);}
int dep[maxn], cur[maxn];
int dfs(int u,int flow,int T){
// printf("%lld\n",u);
if(u == T)return flow;
int rest = 0, tmp = 0;
for(int i = cur[u];i && flow;i = e[i].nexte){
cur[u] = i; int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && (dep[v] == dep[u] + 1)){
tmp = dfs(v,min(flow,e[i].cap - e[i].flow),T);
if(tmp == 0)dep[v] = INF;
e[i].flow += tmp; e[i ^ 1].flow -= tmp;
flow -= tmp;rest += tmp;
if(!flow)return rest;
}
}
return rest;
}
bool bfs(int S,int T){
queue<int> que;
for(int i = 1;i <= T;i++){dep[i] = INF;cur[i] = 0;}
que.push(S);dep[S] = 1; cur[S] = head[S];
while(!que.empty()){
int u = que.front(); que.pop();
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && dep[v] == INF){
que.push(v);
cur[v] = head[v];
dep[v] = dep[u] + 1;
if(v == T)return 1;
}
}
}
return 0;
}
int Dinic(int S,int T){
int mxflow = 0;
while(bfs(S,T)){mxflow += dfs(S,INF,T);}
return mxflow;
}
inline int getid(int x,int y){return (x - 1) * m + y;}
const int dx[4] = { 0,-1, 1, 0};
const int dy[4] = {-1, 0, 0, 1};
signed main(){
n = read(); m = read();int sum = 0, S = getid(n, m) + 1, T = S + 1;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
int x = read();
if((i + j) & 1){
addd(S,getid(i, j),x);
for(int k = 0;k < 4;k++){
int nx = i + dx[k], ny = j + dy[k];
if(nx < 1 || nx > n || ny < 1 || ny > m)continue;
addd(getid(i,j),getid(nx,ny),INF);
}
}
else addd(getid(i,j),T,x);
sum += x;
}
}
printf("%lld\n",sum - Dinic(S,T));
return 0;
}
T3
题意
W 教授正在为国家航天中心计划一系列的太空飞行。每次太空飞行可进行一系列商业性实验而获取利润。现已确定了一个可供选择的实验集合 $ E = { E_1, E_2, \cdots, E_m } $,和进行这些实验需要使用的全部仪器的集合 $ I = { I_1, I_2, \cdots, I_n } $。实验 $ E_j $ 需要用到的仪器是 $ I $ 的子集 $ R_j \subseteq I $。
配置仪器 $ I_k $ 的费用为 $ c_k $ 美元。实验 $ E_j $ 的赞助商已同意为该实验结果支付 $ p_j $ 美元。W 教授的任务是找出一个有效算法,确定在一次太空飞行中要进行哪些实验并因此而配置哪些仪器才能使太空飞行的净收益最大。这里净收益是指进行实验所获得的全部收入与配置仪器的全部费用的差额。
对于给定的实验和仪器配置情况,编程找出净收益最大的试验计划。
题解
最大权闭合子图模板,不做过多解释,自行百度。
代码
#include<bits/stdc++.h>
// #define int long long
using namespace std;
inline int read(){
int x = 0, f =1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 5e2 + 10,maxm = 5e5 + 10, INF = 0x3f3f3f3f;
int n, m;
int id[maxn][maxn], total;
int head[maxm / 10], tot = 1;
struct edge{
int to, nexte, cap, flow;
edge(int to = 0,int ne = 0,int ca = 0,int fl = 0):to(to),nexte(ne),cap(ca),flow(fl){}
}e[maxm * 2];
void add(int u,int v,int cap){e[++tot] = edge(v,head[u],cap);head[u] = tot;}
void addd(int u,int v,int cap){add(u,v,cap);add(v, u, 0);}
int dep[maxm / 10], cur[maxm / 10];
int dfs(int u,int flow,int T){
// printf("%lld\n",u);
if(u == T)return flow;
int rest = 0, tmp = 0;
for(int i = cur[u];i && flow;i = e[i].nexte){
cur[u] = i; int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && (dep[v] == dep[u] + 1)){
tmp = dfs(v,min(flow,e[i].cap - e[i].flow),T);
if(tmp == 0)dep[v] = INF;
e[i].flow += tmp; e[i ^ 1].flow -= tmp;
flow -= tmp;rest += tmp;
if(!flow)return rest;
}
}
return rest;
}
bool bfs(int S,int T){
queue<int> que;
for(int i = 1;i <= T;i++){dep[i] = INF;cur[i] = 0;}
que.push(S);dep[S] = 1; cur[S] = head[S];
while(!que.empty()){
int u = que.front(); que.pop();
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && dep[v] == INF){
que.push(v);
cur[v] = head[v];
dep[v] = dep[u] + 1;
if(v == T)return 1;
}
}
}
return 0;
}
int Dinic(int S,int T){
int mxflow = 0;
while(bfs(S,T)){mxflow += dfs(S,INF,T);}
return mxflow;
}
signed main(){
m = read(); n = read();int ans = 0;
int S = n + m + 1, T = n + m + 2;
for(int i = 1;i <= m;i++){
int x = read();ans += x;addd(S,i,x);
char tools[10000];
memset(tools,0,sizeof(tools));
cin.getline(tools,10000);
int ulen = 0,tool;
while(sscanf(tools + ulen,"%d",&tool) == 1){
addd(i,tool + m,INF);
if(tool == 0)ulen++;
else while(tool){tool /= 10;ulen++;}
ulen++;
}
}
for(int i = 1;i <= n;i++)addd(i + m,T,read());
ans = ans - Dinic(S,T);Dinic(S,T);
for(int i = 1;i <= m;i++){
if(dep[i] != INF)printf("%d ",i);
}
puts("");
for(int i = 1;i <= n;i++){
if(dep[i + m] != INF)printf("%d ",i);
}
printf("\n%d\n",ans);
return 0;
}
T4
题意
现在小朋友们最喜欢的"喜羊羊与灰太狼"。话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:
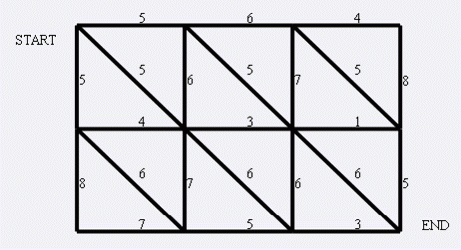
左上角点为 \((1,1)\),右下角点为 \((N,M)\)(上图中 \(N=3\),\(M=4\))。有以下三种类型的道路:
- \((x,y)\rightleftharpoons(x+1,y)\)
- \((x,y)\rightleftharpoons(x,y+1)\)
- \((x,y)\rightleftharpoons(x+1,y+1)\)
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的。左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角 \((1,1)\) 的窝里,现在它们要跑到右下角 \((N,M)\) 的窝中去,狼王开始伏击这些兔子。当然为了保险起见,如果一条道路上最多通过的兔子数为 \(K\),狼王需要安排同样数量的 \(K\) 只狼,才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。
题解
发现直接跑最小割是T飞的。
然后发现这张图很特殊,如果将每个三角形看作点,相邻三角形之间连接长度为相邻边长长度的边,最小割就被转化成最短路。
代码
#include<bits/stdc++.h>
// #define int long long
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f= -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2e3 + 10, maxp = maxn * maxn;
int n, m;
int id[maxn][maxn], cntnod;
int S , T;
int head[maxp], tot;
struct edge{
int to, nexte, wei;
edge(int to = 0,int ne = 0,int we = 0):to(to),nexte(ne),wei(we){}
}e[maxp << 1];
void add(int u,int v,int w){e[++tot] = edge(v, head[u],w);head[u] = tot;}
void addd(int u,int v,int w){add(u, v, w);add(v, u, w);}
struct node{
int first, second;
friend bool operator > (node a,node b){return a.first != b.first ? a.first > b.first : a.second > b.second;}
friend bool operator < (node a,node b){return a.first != b.first ? a.first < b.first : a.second < b.second;}
node(int f = 0,int s = 0):first(f),second(s){}
};
int dis[maxp];bool book[maxp];
priority_queue<node, vector<node> , greater<node> > que;
signed main(){
n = read(); m = read();
for(int i = 1;i < n;i++){
for(int j = 1;j <= (m - 1) * 2;j++){
id[i][j] = ++cntnod;
}
}
S = ++cntnod; T = ++cntnod;int val;
for(int i = 1;i <= n;i++){
for(int j = 1;j < m;j++){
val = read();
if(i == 1){add(S, id[1][2 * j], val);}
else if(i == n){add(id[n - 1][j * 2 - 1], T, val);}
else{addd(id[i - 1][2 * j - 1],id[i][2 * j],val);}
}
}
for(int i = 1;i < n;i++){
for(int j = 1;j <= m;j++){
val = read();
if(j == 1){add(id[i][1],T,val);}
else if(j == m){add(S,id[i][2 * m - 2],val);}
else {addd(id[i][j * 2 - 1],id[i][j * 2 - 2],val);}
}
}
for(int i = 1;i < n;i++){
for(int j = 1;j < m;j++){
val = read();
addd(id[i][2 * j - 1],id[i][2 * j],val);
}
}
memset(dis,0x3f,sizeof(dis));dis[S] = 0;
que.push(node(dis[S],S));
while(!que.empty()){
int u = que.top().second; que.pop();
if(book[u])continue;book[u] = 1;
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to, w = e[i].wei;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
que.push(node(dis[v],v));
}
}
}
printf("%d\n",dis[T]);
return 0;
}
T5
题意
经过千辛万苦小 A 得到了一块切糕,切糕的形状是长方体,小 A 打算拦腰将切糕切成两半分给小 B。出于美观考虑,小 A 希望切面能尽量光滑且和谐。于是她找到你,希望你能帮她找出最好的切割方案。
出于简便考虑,我们将切糕视作一个长 \(P\)、宽 \(Q\)、高 \(R\) 的长方体点阵。我们将位于第 \(z\) 层中第 \(x\) 行、第 \(y\) 列上的点称 \((x,y,z)\),它有一个非负的不和谐值 \(v(x,y,z)\)。一个合法的切面满足以下两个条件:
- 与每个纵轴(一共有 \(P\times Q\) 个纵轴)有且仅有一个交点。即切面是一个函数 \(f(x,y)\),对于所有 \((x,y)(x\in [1,P],y\in[1,Q])\),我们需指定一个切割点 \(f(x,y)\),且 \(1\le f(x,y)\le R\)。
- 切面需要满足一定的光滑性要求,即相邻纵轴上的切割点不能相距太远。对于所有的 \(1\le x,x'\le P\) 和 \(1\le y,y'\le Q\),若 \(|x-x'|+|y-y'|=1\),则 \(|f(x,y)-f(x',y')| \le D\),其中 \(D\) 是给定的一个非负整数。
可能有许多切面 \(f\) 满足上面的条件,小 A 希望找出总的切割点上的不和谐值最小的那个。
题解
设 \((u,v,w)\) 表示连接一条 \(u\to v\),容量为 \(w\) 的边。
发现将每个 \((x,y)\) 的所有 \(z\) 坐标连成一个串(即依次连接 \((S,(x,y,1),\inf),((x,y,1),(x,y,2),v_{x,y,1}),\dots,((x,y,z),T,v_{x,y,z})\)),那么如果没有第二个限制,直接跑最小割即可。
但是第二个限制加进来怎么做呢?
发现我们只需要让割断 \((x,y,z),(u,v,w),(|x-u|+|y-v|=1,|z-w|>D)\) 时,\(S,T\) 联通即可。
然后发现连一条 \(((u,v,w),(x,y,z),\inf)\) 就直接完事了。当然让 \(|z-w|=D\) 即可,没必要连太多的边,限制的效果都一样。
代码
#include<bits/stdc++.h>
//#define int long long
using namespace std;
inline int read(){
int x = 0, f =1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 40 * 40 * 40 + 100,maxm = 2e6 + 10, INF = 0x3f3f3f3f;
int D, x, y, z;
int head[maxn], tot = 1;
struct edge{
int to, nexte, cap, flow;
edge(int to = 0,int ne = 0,int ca = 0,int fl = 0):to(to),nexte(ne),cap(ca),flow(fl){}
}e[maxm * 2];
void add(int u,int v,int cap){e[++tot] = edge(v,head[u],cap);head[u] = tot;}
void addd(int u,int v,int cap){add(u,v,cap);add(v, u, 0);}
int total, id[41][41][41];
int val[41][41][41];
inline int getid(int x,int y,int z){
if(id[x][y][z])return id[x][y][z];
return id[x][y][z] = ++total;
}
int dep[maxn], cur[maxn];
int dfs(int u,int flow,int T){
// printf("%lld\n",u);
if(u == T)return flow;
int rest = 0, tmp = 0;
for(int i = cur[u];i && flow;i = e[i].nexte){
cur[u] = i; int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && (dep[v] == dep[u] + 1)){
tmp = dfs(v,min(flow,e[i].cap - e[i].flow),T);
if(tmp == 0)dep[v] = INF;
e[i].flow += tmp; e[i ^ 1].flow -= tmp;
flow -= tmp;rest += tmp;
if(!flow)return rest;
}
}
return rest;
}
bool bfs(int S,int T){
queue<int> que;
for(int i = 1;i <= total;i++){dep[i] = INF;cur[i] = 0;}
que.push(S);dep[S] = 1; cur[S] = head[S];
while(!que.empty()){
int u = que.front(); que.pop();
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && dep[v] == INF){
que.push(v);
cur[v] = head[v];
dep[v] = dep[u] + 1;
if(v == T)return 1;
}
}
}
return 0;
}
int Dinic(int S,int T){
int mxflow = 0;
while(bfs(S,T)){mxflow += dfs(S,INF,T);}
return mxflow;
}
const int dx[4] = { 0,-1, 1, 0};
const int dy[4] = {-1, 0, 0, 1};
signed main(){
x = read(); y = read(); z = read();
D = read();int S = ++total;int T = ++total;
for(int k = 1;k <= z;k++){
for(int i = 1;i <= x;i++){
for(int j = 1;j <= y;j++){
val[i][j][k] = read();
if(k != z){addd(getid(i,j,k),getid(i,j,k + 1),val[i][j][k]);}
else addd(getid(i,j,k),T,val[i][j][k]);
if(k == 1){addd(S,getid(i,j,k),INF);}
if(k > D)
for(int l = 0;l < 4;l++){
int nx = i + dx[l], ny = j + dy[l];
if(nx < 1 || nx > x || ny < 1 || ny > y)continue;
addd(getid(i,j,k),getid(nx,ny,k - D),INF);
}
}
}
}
printf("%d\n",Dinic(S,T));
return 0;
}
T6
题意
申奥成功后,布布经过不懈努力,终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难题:为即将启动的奥运新项目招募一批短期志愿者。经过估算,这个项目需要 \(n\) 天才能完成,其中第 \(i\) 天至少需要 \(a_i\) 个人。布布通过了解得知,一共有 \(m\) 类志愿者可以招募。其中第 \(i\) 类可以从第 \(s_i\) 天工作到第 \(t_i\) 天,招募费用是每人 \(c_i\) 元。新官上任三把火,为了出色地完成自己的工作,布布希望用尽量少的费用招募足够的志愿者,但这并不是他的特长!于是布布找到了你,希望你帮他设计一种最优的招募方案。
题解
设 \((u,v,w,cost)\) 表示连接一条 \(u\to v\),容量是 \(w\),费用是 \(cost\) 的边。
先给建图方式,然后再说原因。
让 \((i,i+1,mx-a_i,0)\),然后让 \((S,1,mx,0),(n+1,T,mx,0)\)。
然后对于每个类型的志愿者 \(s,t,c\),连接 \((s,t + 1,\inf,c)\)。
其中 \(mx\) 取一个较大值,但是数量级小于 \(\inf\)。
理由:我们发现最大流一定是 \(mx\),然后对于每一天,截下与当天有关的所有边,所有流量加起来一定是 \(mx\),而我们构造的边已经流过 \(mx-a_i\) 的流量了,剩下的边一定流过 \(a_i\) 的流量,故正确。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + ch - '0';ch = getchar();}
return x * f;
}
const int maxn = 5e3 + 10, maxm = 5e4 + 10, INF = 0x3f3f3f3f3f3f3f3f;
int n, m;
int head[maxn], tot = 1;
struct edge{
int to, nexte, cap,flow, cost;
edge(int t = 0,int ne = 0,int ca = 0,int co = 0,int fl = 0):to(t),nexte(ne),cap(ca),flow(fl),cost(co){}
}e[maxm * 2];
void add(int u,int v,int cap,int cost){e[++tot] = edge(v,head[u],cap,cost);head[u] = tot;}
void addd(int u,int v,int cap,int cost){add(u,v,cap,cost);add(v,u,0,-cost);}
int pre[maxn];
bool book[maxn];
int dis[maxn];
bool SPFA(int S,int T){
// puts("IN");
queue<int> que;
// memset(dis,0x3f,sizeof(dis));
for(int i = 1;i <= n + 3;i++)dis[i] = INF;
memset(book,0,sizeof(book));
memset(pre,0,sizeof(pre));
que.push(S);book[S] = true;dis[S] = 0;
while(!que.empty()){
// puts("111111111");
int u = que.front();que.pop();book[u] = false;
// printf("head:%d\n",u);
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
// printf("%d ->%d,%d %d %d %d %d\n",i,e[i].to,e[i].cap,e[i].flow,dis[v],dis[u],e[i].cost);
if((e[i].cap > e[i].flow) && (dis[v] > dis[u] + e[i].cost)){
pre[v] = i;dis[v] = dis[u] + e[i].cost;
if(!book[v]){que.push(v);book[v] = true;}
}
}
}
return pre[T] != 0;
}
pair<int,int> MCMF(int S,int T){
int mincost = 0, maxflow = 0;
while(SPFA(S,T)){
// puts("times");
int fl = INF;
for(int i = pre[T];i;i = pre[e[i ^ 1].to]){
fl = min(fl,e[i].cap - e[i].flow);
// printf("%d %d\n",fl,e[i ^ 1].to);
}
mincost += fl * dis[T];maxflow += fl;
for(int i = pre[T];i;i = pre[e[i ^ 1].to]){
e[i].flow += fl;
e[i ^ 1].flow -= fl;
}
}
return make_pair(mincost, maxflow);
}
int a[maxn];
signed main(){
n = read(); m = read();int S = n + 3, T = n + 2,tt = n + 1;
for(int i = 1;i <= n;i++)a[i] = read();
int inf = 0x3f3f3f3f3f;addd(S,1,inf,0);addd(tt,T,inf,0);
for(int i = 1;i <= n;i++){addd(i,i + 1,inf - a[i],0);}
for(int i = 1;i <= m;i++){
int u = read(), v = read(), w = read();
addd(u, v + 1, INF, w);
}
printf("%lld\n",MCMF(S,T).first);
return 0;
}
T7
T8
T9
题意
P6943 [ICPC2018 WF] Conquer The World
给定一个 \(n\) 点 \(n-1\) 边的无向图,每条边 \((u,v)\) 有边权 \(c\)。
现在第 \(i\) 个点有 \(x_i\) 的点权,每个点需要 \(y_i\) 的点权,所以你可以移动点权到不同的点上。移动一条边上的点 \(u\) 的 \(k\) 个单位点权到 \(v\) 要用 \(k \times c\) 的代价。
求满足所有点的需要的最小代价。
\(1 \le n \le 2.5 \times 10^5\),\(1 \le u,v \le n\),\(1 \le c \le 10^6\),\(0 \le \sum y_i\le \sum x_i \le 10^6\)。
题解
这个有着显然的网络流建模方法:
首先将每条边连接双向的网络流边,容量正无穷,费用就是边权。
然后对于每个点,如果剩余点权为正,就向汇点连边,如果剩余点权为负,则从源点连边。
然后跑最小费用最大流即可。
但是现在的 \(n\le2.5\times10^5\),怎么办呢?
考虑一个性质,就是所有的路径一定不会交叉。
考虑反悔贪心,如果设现在所在节点是 \(x\),那么将深度最小的源点和汇点相匹配,尝试流一个流量,费用显然好算。
然后考虑如何反悔,很简单,对于一次匹配 \((i,j)\),就让 \(2\times dep_x-dep_i\) 和 \(2\times dep_x-dep_j\) 加入一个堆中,这样的话只要后来选择了其中一个点,那么这对匹配的贡献就减除了。
然后每次向上进行合并以及进行决策的时候用左偏堆维护即可,合并和查询都是 \(O(\log n)\) 的。
哦对了,因为每个需求点一定需要匹配,那么就让加入的 \(dep_x\) 再减去 \(INF\),这样一定是最小的,就一定能够匹配上。
代码
#include<bits/stdc++.h>
#include<ext/pb_ds/priority_queue.hpp>
#define ll long long
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2.5e5 + 10;
const ll INF = 1e13;
int n;
ll x[maxn], y[maxn];
int tot, head[maxn];
struct edge{
int to, nexte;ll wei;
edge(int to = 0,int ne = 0,ll we = 0):to(to),nexte(ne),wei(we){}
}e[maxn << 1];
void add(int u,int v,ll w){e[++tot] = edge(v,head[u],w);head[u] = tot;}
ll ans, cnt, dep[maxn];
__gnu_pbds::priority_queue<ll,greater<ll> > A[maxn],B[maxn];
void dfs(int u,int f){
for(int i = x[u] + 1;i <= y[u];i++)
A[u].push(dep[u] - INF),cnt++;
for(int i = y[u] + 1;i <= x[u];i++)
B[u].push(dep[u]);
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;ll w = e[i].wei;
if(v == f)continue;
dep[v] = dep[u] + w;dfs(v, u);
A[u].join(A[v]);B[u].join(B[v]);
}
while(!A[u].empty() && !B[u].empty() && A[u].top() + B[u].top() < 2LL * dep[u]){
ll xx = A[u].top(), yy = B[u].top(); A[u].pop(); B[u].pop();
ans += xx + yy - 2LL * dep[u];
A[u].push(2 * dep[u] - yy);B[u].push(2 * dep[u] - xx);
}
}
signed main(){
n = read();int u, v, w;
for(int i = 1;i < n;i++){
u = read();v = read(); w = read();
add(u, v, w);add(v, u, w);
}
for(int i = 1;i <= n;i++){x[i] = read();y[i] = read();}
dfs(1 ,1);
printf("%lld\n",ans + cnt * INF);
return 0;
}
T10
题意
曾经有一款流行的游戏,叫做 Infinity Loop,先来简单的介绍一下这个游戏:
游戏在一个 \(n \times m\) 的网格状棋盘上进行,其中有些小方格中会有水管,水管可能在格某些方向的边界的中点有接口,所有水管的粗细都相同,所以如果两个相邻方格的共边界的中点都有接头,那么可以看作这两个接头互相连接。水管有以下 \(15\) 种形状:

游戏开始时,棋盘中水管可能存在漏水的地方。
形式化地:如果存在某个接头,没有和其它接头相连接,那么它就是一个漏水的地方。
玩家可以进行一种操作:选定一个含有非直线型水管的方格,将其中的水管绕方格中心顺时针或逆时针旋转 \(90\) 度。
直线型水管是指左图里中间一行的两种水管。
现给出一个初始局面,请问最少进行多少次操作可以使棋盘上不存在漏水的地方。
题解
其实很难想到这玩应是费用流
考虑如何刻画不漏水这一情况。
发现如果将图黑白染色,然后每个点向四个方向再新建四个虚点(方向映射为 \(L,D,R,U=0,1,2,3\),下文中称 \((1,i,j)\) 表示点 \((i,j)\) 向下新建的虚点,其他同理),然后按照题中给出的方式,黑点从源点连边到相应虚点,白点同理,相邻的点从黑点向白点连接相邻的虚点,那么不漏水当且仅当 最大流 \(\times 2=\)总虚点数。
然后考虑如何刻画旋转情况和花费。
这里只讨论黑点,白点将所有边反过来。
按照新建出的虚点数量分类讨论:
- \(0\) 个虚点:不用管直接 \(continue\) 即可。
- \(4\) 个虚点:旋转不了建完边也直接 \(continue\)。
- \(1\) 个虚点:设这个方向是 \(p\in[0,3]\),然后发现旋转到两边只需要一个花费,而旋转到相反方向需要两个花费。怎么办呢?直接让虚点 \((i,j,p)\) 向相邻的两个虚点连一条费用、容量都是 \(1\) 的即可。然后向相反的方向连接一条费用是 \(2\),容量是 \(1\) 的边即可。简单想想就知道这个就是强行将方向转过去的意思。
- \(2\) 个虚点:如果方向正好相反建完边也直接 \(continue\),否则有方向的两个虚点分别向相反的方向连一条容量、费用都是 \(1\) 的边。简单想想就知道是对的。
- \(3\) 个虚点:本质上是和 \(1\) 个虚点情况互补的,连的边有两种:一种是让两个相反方向的虚点向空下来的那个虚点连边,容量费用都是 \(1\),另一种是直接让于空下来虚点相反的那个虚点与空下来的虚点连边,费用 \(2\) 容量 \(1\)。
然后就没了。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f =1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 5e4 + 10, maxm = 1e6 + 10, INF = 0x3f3f3f3f;
int n, m;
int head[maxn], tot = 1;
struct edge{
int to, nexte, cap,flow, cost;
edge(int t = 0,int ne = 0,int ca = 0,int co = 0,int fl = 0):to(t),nexte(ne),cap(ca),flow(fl),cost(co){}
}e[maxm * 2];
inline void add(int u,int v,int cap,int cost){e[++tot] = edge(v,head[u],cap,cost);head[u] = tot;}
inline void addd(int u,int v,int cap,int cost){add(u,v,cap,cost);add(v,u,0,-cost);}
int pre[maxn];
bool book[maxn];
int dis[maxn];
int total;
bool SPFA(int S,int T){
queue<int> que;
for(int i = 1;i <= total;i++)dis[i] = INF;
memset(book,0,sizeof(book));
memset(pre,0,sizeof(pre));
que.push(S);book[S] = true;dis[S] = 0;
while(!que.empty()){
int u = que.front();que.pop();book[u] = false;
// printf("head:%d\n",u);
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
// printf("%d ->%d,%d %d %d %d %d\n",i,e[i].to,e[i].cap,e[i].flow,dis[v],dis[u],e[i].cost);
if((e[i].cap > e[i].flow) && (dis[v] > dis[u] + e[i].cost)){
pre[v] = i;dis[v] = dis[u] + e[i].cost;
if(!book[v]){que.push(v);book[v] = true;}
}
}
}
return pre[T] != 0;
}
pair<int,int> MCMF(int S,int T){
int mincost = 0, maxflow = 0;
while(SPFA(S,T)){
int fl = INF;
for(int i = pre[T];i;i = pre[e[i ^ 1].to]){
fl = min(fl,e[i].cap - e[i].flow);
// printf("%d %d\n",fl,e[i ^ 1].to);
}
mincost += fl * dis[T];maxflow += fl;
for(int i = pre[T];i;i = pre[e[i ^ 1].to]){
e[i].flow += fl;
e[i ^ 1].flow -= fl;
}
}
return make_pair(mincost, maxflow);
}
vector<vector<int> >id[4];
//0=l,1=d,2=r,3=u
const int dx[4] = { 0, 1, 0,-1};
const int dy[4] = {-1, 0, 1, 0};
signed main(){
n = read();m = read();int S = ++total;
for(int k = 0;k < 4;k++){
id[k].resize(n + 1);
for(int i = 1;i <= n;i++){
id[k][i].resize(m + 1);
for(int j = 1;j <= m;j++){
id[k][i][j] = ++total;
// printf("(%d,%d,%d) = %d\n",i,j,k,id[k][i][j]);
}
}
}
int T = ++total, res = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if((i + j) & 1){
for(int k = 0;k < 4;k++){
int nx = dx[k] + i,ny = dy[k] + j;
if(nx < 1 || nx > n || ny < 1 || ny > m)continue;
addd(id[k][i][j],id[(k + 2) % 4][nx][ny],1,0);
}
}
int opt = read();
int x[4] = {(opt >> 3) & 1,(opt >> 2) & 1,(opt >> 1) & 1,opt & 1};
int sum = x[0] + x[1] + x[2] + x[3];
// printf("(%d,%d) : %d %d %d %d\n",i,j,x[0],x[1],x[2],x[3]);
res += sum;
if(sum == 0)continue;
if(sum == 1){
int p = 0;if(x[1])p = 1;if(x[2])p = 2;if(x[3])p = 3;
if((i + j) & 1){
addd(S,id[p][i][j],1,0);
addd(id[p][i][j],id[(p + 1) % 4][i][j],1,1);
addd(id[p][i][j],id[(p + 2) % 4][i][j],1,2);
addd(id[p][i][j],id[(p + 3) % 4][i][j],1,1);
}
else{
addd(id[p][i][j],T,1,0);
addd(id[(p + 1) % 4][i][j],id[p][i][j],1,1);
addd(id[(p + 2) % 4][i][j],id[p][i][j],1,2);
addd(id[(p + 3) % 4][i][j],id[p][i][j],1,1);
}
}
if(sum == 2){
int p = x[1], q = x[3] + 2;
if(!x[p]){p = 2, q = 3;}
if(!x[q]){p = 0, q = 1;}
if((i + j) & 1){
addd(S,id[p][i][j],1,0);
addd(S,id[q][i][j],1,0);
}
else{
addd(id[p][i][j],T,1,0);
addd(id[q][i][j],T,1,0);
}
if(q - p == 2)continue;
if((i + j) & 1){
addd(id[p][i][j],id[(p + 2) % 4][i][j],1,1);
addd(id[q][i][j],id[(q + 2) % 4][i][j],1,1);
}
else{
addd(id[(p + 2) % 4][i][j],id[p][i][j],1,1);
addd(id[(q + 2) % 4][i][j],id[q][i][j],1,1);
}
}
if(sum == 3){
int p = 0;if(!x[1])p = 1;if(!x[2])p = 2;if(!x[3])p = 3;
for(int k = 0;k < 4;k++){
if(k == p)continue;
if((i + j) & 1){addd(S,id[k][i][j],1,0);}
else{addd(id[k][i][j],T,1,0);}
}
if((i + j) & 1){
addd(id[(p + 1) % 4][i][j],id[p][i][j],1,1);
addd(id[(p + 2) % 4][i][j],id[p][i][j],1,2);
addd(id[(p + 3) % 4][i][j],id[p][i][j],1,1);
}
else{
addd(id[p][i][j],id[(p + 1) % 4][i][j],1,1);
addd(id[p][i][j],id[(p + 2) % 4][i][j],1,2);
addd(id[p][i][j],id[(p + 3) % 4][i][j],1,1);
}
}
if(sum == 4){
for(int k = 0;k < 4;k++){
if((i + j) & 1){addd(S,id[k][i][j],1,0);}
else{addd(id[k][i][j],T,1,0);}
}
}
}
}
auto ans = MCMF(S,T);
if(ans.second != res / 2){puts("-1");}
else{printf("%d\n",ans.first);}
// for(int u = 1;u <= total;u++){
// printf("u = %d\n",u);
// for(int i = head[u];i;i = e[i].nexte){
// printf("-> %d,cap = %d, flow = %d, cost = %d\n",e[i].to,e[i].cap,e[i].flow,e[i].cost);
// }
// }
return 0;
}
T11
T12
题意
有 \(n\) 个技能,\(m\) 个成就。每个技能有一个等级,初始均为 \(1\)。
你可以用 \(c_i\) 块钱令技能 \(i\) 提升一个等级,该操作没有次数限制。
第 \(i\) 个成就达成的条件是对于 $\forall j\in [1,n],level_j \ge L_{i,j} $,其中 \(level_j\) 表示第 \(j\) 个技能的等级。达成成就 \(i\) 后,你会获得 \(a_i\) 元的奖励。
请最大化获得的奖励与所需成本之差,并输出该值。
\(n,m\le 50,\, 1\le L_{i,j}\le 5,\, 1\le a_i,c_i\le 10^6\)。
题解
构建这样一个图:\(S\to (i,5) \to (i,4) \to \cdots \to (i,1)\),容量依次是 \(4\times c_i,3\times c_i,\cdots,0\)。
然后每个限制检出一个新点 \(p\),然后让 \((j,L_{i,j})\to p\),容量都是 \(inf\),最后让 \(p\to T\),容量是 \(a_i\)。
然后跑个最小割就没了。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f =1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 5e2 + 10,maxm = maxn * maxn, INF = 0x3f3f3f3f;
int n, m;
int head[maxn], tot = 1 , total;
struct edge{
int to, nexte, cap, flow;
edge(int to = 0,int ne = 0,int ca = 0,int fl = 0):to(to),nexte(ne),cap(ca),flow(fl){}
}e[maxm * 2];
void add(int u,int v,int cap){e[++tot] = edge(v,head[u],cap);head[u] = tot;}
void addd(int u,int v,int cap){add(u,v,cap);add(v, u, 0);}
int dep[maxn], cur[maxn];
int dfs(int u,int flow,int T){
// printf("%d\n",u);
if(u == T)return flow;
int rest = 0, tmp = 0;
for(int i = cur[u];i && flow;i = e[i].nexte){
cur[u] = i; int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && (dep[v] == dep[u] + 1)){
tmp = dfs(v,min(flow,e[i].cap - e[i].flow),T);
if(tmp == 0)dep[v] = INF;
e[i].flow += tmp; e[i ^ 1].flow -= tmp;
flow -= tmp;rest += tmp;
if(!flow)return rest;
}
}
return rest;
}
bool bfs(int S,int T){
queue<int> que;
for(int i = 1;i <= total;i++){dep[i] = INF;cur[i] = 0;}
que.push(S);dep[S] = 1; cur[S] = head[S];
while(!que.empty()){
int u = que.front(); que.pop();
for(int i = head[u];i;i = e[i].nexte){
int v = e[i].to;
if(e[i].cap - e[i].flow > 0 && dep[v] == INF){
que.push(v);
cur[v] = head[v];
dep[v] = dep[u] + 1;
if(v == T)return 1;
}
}
}
return 0;
}
int Dinic(int S,int T){
int mxflow = 0;
while(bfs(S,T)){mxflow += dfs(S,INF,T);}
return mxflow;
}
int id[maxn][6], c[maxn];
signed main(){
int S = ++total, T = ++total, sum = 0;
n = read(); m = read();
for(int i = 1;i <= n;i++){
c[i] = read();
for(int j = 1;j <= 5;j++)id[i][j] = ++total;
for(int j = 5;j - 1;j--){addd(id[i][j],id[i][j - 1],(j - 2) * c[i]);}
addd(S,id[i][5],4 * c[i]);
}
for(int i = 1;i <= m;i++)sum += (c[i] = read());
for(int i = 1;i <= m;i++){
int p = ++total;addd(p,T,c[i]);
for(int j = 1;j <= n;j++)addd(id[j][read()],p,INF);
}
printf("%d\n",sum - Dinic(S,T));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号