CF1368题解
CF1368
ABC略。
CF1368D
CF1368D题意
给定 \(n\) 个非负整数 \(a_1,\cdots,a_n\)。
你可以进行如下操作:选择两个不同的下标 \(i,j\) 满足 \(1\leq i,j\leq n\),并将 \(a_i\gets a_i\ \mathsf{AND}\ a_j,\ a_j\gets a_i\ \mathsf{OR}\ a_j\),两个赋值同时进行。AND 是按位与,OR 是按位或。
你可以进行任意次操作。求操作后所有数的平方和的最大值,即 \(\max \sum a_i^2\)。
CF1368D题解
首先观察这个操作,不难发现其实就是将一个数在二进制位中的 \(0\) 位尽可能用另一个数相同位置的 \(1\) 填入。
而且,因为是平方和最大,那么尽可能的填满一个数一定更优。
没了。
CF1368D代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2e5 + 10;
int n, a[maxn];
int buc[30];
signed main(){
n = read();
for(int i = 1;i <= n;i++){
a[i] = read();
for(int j = 20;j + 1;j--)
if(a[i] & (1 << j))buc[j]++;
a[i] = 0;
}
long long sum = 0;
for(int i = 1;i <= n;i++){
for(int j = 20;j + 1;j--)
if(buc[j]){a[i] |= (1 << j);buc[j]--;}
sum += (long long)a[i] * a[i];
}
printf("%lld\n",sum);
return 0;
}
CF1368E
CF1368E题意
有一个由 \(n\) 个点 \(m\) 条边组成的有向无环图,每个点出度至多为2。您需要标记一些点(不超过 \(\frac{4}{7}n\) 个)。标记一个点 \(u\) 将会删除所有与 \(u\) 连接的边。
您需要找到一种标记点的方案,使得删边后的图中每一条路径至多有一条边。
CF1368E题解
神仙思路真想不到。
首先观察可知 \(7=4+2+1\),也就是说,如果我们能够将整张图的所有点分成 \(A,B,C\) 三个集合,且满足 \(|C|<2|B|<4|A|\),那么就一定有 \(|C|<\frac{4}{7}n\)。
尝试构造这样一个集合。
对于所有点,将它们分成三类:
- 第一类:入度为零或者入边全都属于第三类。
- 第二类:入边至少有一条是第一类,剩下的都不是第二类。
- 第三类:剩下的。
不难发现,将集合分成这三类之后,删除第三类就一定能够满足题目限制。
现在尝试证明第三类的总点数少于 \(\frac{4}{7}n\)。
首先,因为每个点的出度最多为 \(2\),那么就必然有 \(2|A|>|B|\)。
同理,有 \(2|B|>|C|\)。
故有 \(|C|<2|B|<4|A|\)。
好神仙的思路,%%%。
CF1368E代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2e5 + 10;
int n, m, col[maxn];
signed main(){
int T = read(), u, v;
while(T--){
n = read(); m = read();
vector<set<int>> fr(n + 1);
for(int i = 1;i <= n;i++)col[i] = 0;
for(int i = 1;i <= m;i++){
u = read(); v= read();
fr[v].insert(u);
}
for(int v = 1;v <= n;v++){
for(int u : fr[v]){
if(col[u] == 1){col[v] = 2;break;}
if(!col[u])col[v] = 1;
}
}
vector<int> ans;ans.clear();
for(int i = 1;i <= n;i++)
if(col[i] == 2)ans.push_back(i);
printf("%d\n",ans.size());
for(int i : ans)printf("%d ",i);
puts("");
}
return 0;
}
CF1368F
CF1368F题意
这是一道交互题。
现在有 \(n\) 盏灯,它们围成一个环。你的任务是尽可能增加亮灯的数量,而交互库会尽可能减少亮灯的数量。
你和交互库会依次进行操作:
- 每次你任意选择 \(k\) 个位置,将这些位置的灯亮起来,或者你决定让游戏结束(注,如果你让游戏结束,那这轮你就不能点亮任何一盏灯,相应的,交互库也会停止操作)。
- 然后交互库会选择一个连续长为 \(k\) 的区间 \([x,x+k-1]\),并把这里的所有灯熄灭。交互库会根据你的操作进行决策。当然,交互库会告诉你它熄灭的灯的起始位置。
你的任务是尽可能增加亮灯的数量,但是交互库已经提前知道了,对于 \(n\) 盏灯,你最多可能亮灯的数量是 \(f(n)\),你需要在不超过 \(10^4\) 轮(你和交互库各进行一次操作称为一轮)之后达到这个值。
\(n\le10^3\)
CF1368F题解
神仙交互题
不难想到,如果每次都让答案增加 \(1\),那么在 \(n\) 轮之后一定能够达到这个上界,于是就不用管次数限制了。
现在的问题是怎么操作才能够使得每次答案都能增加 \(1\)。
首先先确定下每次的 \(k\)。
如果对序列的每一位,希望最终答案亮灯的是 \(1\),不亮灯的是 \(0\)。
那么最终序列一定形如 \(111\dots0(k-1个1)111\dots0(k-1个1)\dots110\)。
然后发现最终的答案 \(ans=n-k^2-1+k(k-1)\),其中 \(k^2\le n\)。
不难发现当 \(k=\lfloor\sqrt{n}\rfloor\) 时,这个答案最大。
然后就没了,每次找被变成 \(0\) 的数字变回来就好了。
CF1368F代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n;
bool a[maxn];
signed main(){
cin >> n;int k = sqrt(n);
for(int tt = 1;tt <= n + 2;tt++){
int cnt = 0;vector<int> opt;opt.clear();
for(int i = 1;i <= n && cnt < k;i++){
if(i % k == 0 || i == n)continue;
if(!a[i]){opt.push_back(i);cnt++;a[i] = 1;}
}
cout << opt.size();for(int i : opt)cout << " " << i;cout << endl;
int x;cin >> x;x--;
for(int i = 1;i <= k;i++){int y = x + i;if(y > n)y -= n;a[y] = 0;}
}
cout << 0 << endl;
return 0;
}
CF1368G
CF1368G题意
有一个 \(n\times m\) 的棋盘,被 \(1\times2\) 的骨牌覆盖,保证 \(2\mid nm\)。
现在你需要执行以下操作:
- 移去恰好一张骨牌。
- 将一张骨牌沿着其长边进行移动。你可以进行这一步任意次。
- 你需要保证在任意时刻,每张骨牌的位置与其初始位置至少有一个公共格子。
求你可以得到的所有可能的局面的数量。
两种局面不同,当且仅当某个位置在其中一者中被骨牌覆盖,而在另一者中没有。
\(nm\le2\times10^5\)。
输入格式为:输入一张大小为 \(n\times m\) 的矩阵,位置 \((i,j)\) 为 L/R/U/D 表示其被一张骨牌的 左/右/上/下 端覆盖。
CF1368G题解
首先先来想一个问题,如果在一个位置 \((x,y)\) 有一个空位,怎么刻画这个空位的移动?
发现如果一个空位站在 \((i,j)\) 能够向四个方向移动,当且仅当 \((i+1,j),(i+2,j)\)(其他方向同理)上面的是同一块骨牌。
然后可以按照这个连接有向边。
我们来考虑下这样连接完之后是什么图。
首先,每个点最多只有一个入度(这个显然,考虑一张骨牌的一头,显然只可能从向另一头方向走两格的位置连过来)
那么这个东西已经是一棵外向基环森林了。
可是真的有环吗?
我们尝试用骨牌拼成一个环。(拿画图做的非常丑陋)
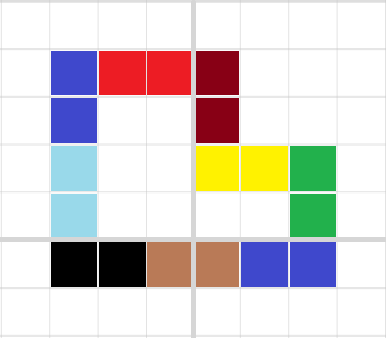
根据pick's theorem,显然有 \(A=i+\frac{b}{2}-1\),其中 \(A\) 是以整点为顶点的多边形面积,\(i\) 是多边形内部格点数量,\(b\) 是边上格点数量。
然后由于组成的图形上下(左右)一一对应,并且每一个骨牌占两格格子,那么显然有 \(4|b\),也就是说,\(2|\frac{b}{2}\)
然后就发现这里面的 \(i\) 一定是奇数,不符合题意。
然后就发现这道题的一个非常厉害的性质:这是个外向森林。
而且将整张图黑白染色之后,发现黑点到不了白点,但是一个骨牌占一个黑点一个白点,也就是说,移除一张骨牌能够得到的局面相当于黑点能到达的位置 \(\times\) 白点能到达的位置。
显然发现每个点能够到达的位置数量就是自己的子树大小。
那么移除一个骨牌能够产生的最终状态(贡献)就是骨牌所在两个点的子树大小的乘积。
不过这里出现一个小问题,我们设 \(((x,y),(u,v))\) 表示最后剩下的两个空位置(钦定第一个是黑点 \(a\),第二个是白点 \(b\)),那么相同的 \(((x,y),(u,v))\) 显然只能统计一次。
不过有的时候会重复统计,怎么办?
发现我们在计算子树大小的时候,顺便标一下每个点的 \(dfs\) 序,这个骨牌的贡献就是使得 \(x\in[dfn_a,dfn_a+siz_a-1],y\in[dfn_b,dfn_b+siz_b-1],(x,y)\) 的最终局面存在。
提示到这了,思路就明显了,直接上扫描线即可。
注意空间开大点啊(
CF1368G代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
bool stmemory;
const int maxn = 4e5 + 10;
int n, m;
inline int getid(int i,int j){return (i - 1) * m + j;}
vector<int> mp[maxn];
//L=0,U=1,R=2,D=3
inline int optid(char ch){if(ch == 'R')return 0;if(ch == 'D')return 1;if(ch == 'L')return 2;if(ch == 'U')return 3;}
const int dx[4] = { 0,-1, 0, 1};
const int dy[4] = {-1, 0, 1, 0};
char ch[maxn];
vector<int> edg[maxn];
int fa[maxn];
int dfn[maxn], idx, low[maxn];
void dfs(int u){dfn[u] = ++idx;for(int v : edg[u])dfs(v);low[u] = idx;}
struct scanline{
int x, y, opt;
scanline(int x = 0,int y = 0,int opt = 0
):x(x),y(y),opt(opt){}
};
vector<scanline> vec[maxn];
struct Segment_Tree{
struct node{
int l, r;int minn, cnt;//minn 是区间tag决定是否用儿子更新,cnt是有面积的位置总数。
node(int l = 0,int r = 0,int minn = 0,int cnt = 0):l(l),r(r),minn(minn),cnt(cnt){}
}d[maxn << 2];
void pushup(int p){
if(d[p].minn){d[p].cnt = d[p].r - d[p].l + 1;}
else d[p].cnt = d[p << 1].cnt + d[p << 1 | 1].cnt;
}
void build(int l,int r,int p){
d[p] = node(l, r);if(l == r)return;
int mid = l + r >> 1;
build(l,mid,p << 1);build(mid + 1,r,p << 1 | 1);
pushup(p);
}
void update(int l,int r,int s,int t,int p,int upd){
if(s <= l && r <= t){d[p].minn += upd;pushup(p);return;}
int mid = l + r >> 1;
if(s <= mid)update(l,mid,s,t,p << 1,upd);
if(mid < t)update(mid + 1,r,s,t,p << 1 | 1,upd);
pushup(p);
}
int query(){return d[1].cnt;}
}tree;
bool edmemory;
signed main(){
cerr << (&stmemory - &edmemory) / 1024.0 / 1024.0 << "Mib cost.\n";
n = read();m = read();
for(int i = 1;i <= n;i++){
mp[i].resize(m + 1); scanf("%s",ch + 1);
for(int j = 1;j <= m;j++) mp[i][j] = optid(ch[j]);
}
// puts("11111111");
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
for(int k = 0;k < 4;k++){
int nx = i + dx[k] * 2, ny = j + dy[k] * 2;
if(nx < 1 || nx > n || ny < 1 || ny > m)continue;
if(mp[nx][ny] != (k + 2) % 4)continue;
edg[getid(i, j)].push_back(getid(nx,ny));
fa[getid(nx,ny)] = getid(i, j);
}
}
}
// puts("22232322222");
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if(!dfn[getid(i,j)]){
int u = getid(i, j);
while(fa[u])u = fa[u];
dfs(u);
}
}
}
// puts("3333343333343");
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if((i + j) & 1){
int nx = dx[mp[i][j]] + i, ny = dy[mp[i][j]] + j;
int xl = dfn[getid(i, j)], xr = low[getid(i, j)];
int yu = dfn[getid(nx,ny)],yd = low[getid(nx,ny)];
// printf("(%d, %d), (%d, %d)\n",i,j,nx,ny);
// printf("%d %d %d %d\n",xl,xr,yu,yd);
vec[xl ].push_back(scanline(yu,yd,1));
vec[xr + 1].push_back(scanline(yu,yd,-1));
}
}
}
// puts("4444444444");
int ans = 0;tree.build(1,idx,1);
for(int i = 1;i <= idx;i++){
for(auto v : vec[i]){tree.update(1,idx,v.x,v.y,1,v.opt);}
ans += tree.query();
}
printf("%lld\n",ans);
return 0;
}
CF1368H1&H2
CF1368H1&H2题意
实验板有 \(n\) 行 \(m\) 列,每个行列交叉处有一个节点。试验板每侧都有端口。左、右侧各 \(n\) 个端口,上、下侧各 \(m\) 个端口。每个端口是红色或蓝色。
端口可通过导线连接。
- 每根导线连接一红色端口和一蓝色端口,每个端口最多连一条导线。
- 导线的每个部分水平或垂直,最多在一个节点处拐弯。
- 导线不能在节点之外的地方和其他导线相交(也不可以和自己相交)。
试验板的容量是根据上述规则导线数量的最大值。
以下是一种可能的连接方式
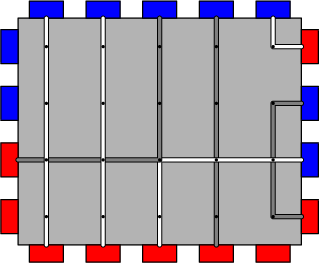
注:Eazy Version下没有修改,也就是说,\(q=0\)。
端口颜色未固定,有 \(q\) 次修改。每次修改,在一条边上的连续区间内,端口颜色反转。
计算每次修改后试验板容量。
\(1\le n,m \le 10^5, 0 \le q \le 10^5\)。
CF1368H1题解
首先大家看到这个东西一定能想到网络流叭!
先主动弱化数据范围,到 \(n\times m\le1000\) 的时候,你会怎么做?
如果将每一个 \((i,j)\) 连向 \((i+1,j),(i,j+1)\),然后跑Dinic,那么最大流,也就是最大匹配,就是最终答案。
让我们回到这道题,现在 \(n,m\le10^5\),显然如果对每个点都连边会T飞的,考虑怎么办。
这个时候我们发现,再考虑最大流已经很困难了,我们不妨考虑最小割。
最小割的实质其实是将整张图的所有点分割成两个点集 \(S\) 和 \(T\)。
我们尝试将 \((x,y)\in S\) 的点 \((x,y)\) 染成黑色。
然后考虑最小割在这个图上的实际意义,其实就是所有黑白点之间边的总长。
说起来可能不太好懂,画张图更加形象。
(这张图省略了四周的颜色,实际上,黑点白点与 \(R,B\) 对应)。
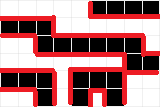
那么图中所有红色边长加起来就是整张图的割的代价啦(画了半天QAQ)
然后我们考虑以下几种优化(到尽可能最小)。
- 这个图中不会出现一个完整的不与边界相连的联通块。
- 同样的,还是上图:
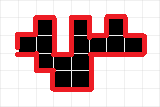
- 发现,如果将这里面所有的黑点改成白点,最小割答案一定变小。
- 这个图中一定不会出现一条路径,使得只沿着黑点,能够从一侧不到达相对侧
.png)
- 不难发现,我们将所有的黑点变成白点一定会更小。
- 这个图中一定不会出现折线
.png)
- 不难发现,将这个折线“捋直了”会更短。
综上所述,如果我们想让割的代价最小,一定是走直线找到最近的点对。
对于行和列都是同理的,这里给出行的做法,列的做法同理。
于是可以设计 \(dp_{i,0/1}\) 表示这一行的颜色是黑色还是白色的最小代价。
递推式
注:\(col\) 是你之前确定好的颜色(就是不能中间改的意思)
初始状态(你强制第 \(0\) 行是什么颜色,这一行的其他颜色就会产生贡献):
当然,如果你行匹配好了,列的就没办法匹配了,如果颜色不相同的话就得加上。
至此,Eazy Version就已经做完了。
CF1368H1代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 1e5 + 10;
int n, m, q;
char ch[maxn];
int L[maxn], R[maxn], U[maxn], D[maxn];
int dp[maxn][2];
signed main(){
n = read(); m = read(); q = read();
scanf("%s",ch + 1);for(int i = 1;i <= n;i++)L[i] = (ch[i] == 'B');
scanf("%s",ch + 1);for(int i = 1;i <= n;i++)R[i] = (ch[i] == 'B');
scanf("%s",ch + 1);for(int i = 1;i <= m;i++)U[i] = (ch[i] == 'B');
scanf("%s",ch + 1);for(int i = 1;i <= m;i++)D[i] = (ch[i] == 'B');
memset(dp,0x3f,sizeof(dp));dp[0][0] = dp[0][1] = 0;
for(int i = 1;i <= m;i++){dp[0][0] += U[i];dp[0][1] += !U[i];}
for(int i = 1;i <= n;i++){
dp[i][0] = min(dp[i - 1][0],dp[i - 1][1] + m) + L[i] + R[i];
dp[i][1] = min(dp[i - 1][1],dp[i - 1][0] + m) + !L[i] + !R[i];
}
for(int i = 1;i <= m;i++){dp[n][0] += D[i];dp[n][1] += !D[i];}
int ans = 0x3f3f3f3f;ans = min(dp[n][0],dp[n][1]);
memset(dp,0x3f,sizeof(dp));dp[0][0] = dp[0][1] = 0;
for(int i = 1;i <= n;i++){dp[0][0] += L[i];dp[0][1] += !L[i];}
for(int i = 1;i <= m;i++){
dp[i][0] = min(dp[i - 1][0],dp[i - 1][1] + n) + U[i] + D[i];
dp[i][1] = min(dp[i - 1][1],dp[i - 1][0] + n) + !U[i] + !D[i];
}
for(int i = 1;i <= n;i++){dp[m][0] += R[i];dp[m][1] += !R[i];}
ans = min(min(dp[m][0],dp[m][1]),ans);
printf("%d\n",ans);
return 0;
}
CF1368H2题解
在向下看之前请确保你已经看完并看懂了H1题解。
现在带上了修改,怎么办呢?
同样的,在这里只说行的做法,列的做法类似。
我们发现,\((L_i,R_i)\) 的取值只有四种,递推式子也只有 \(2\times2\) 这么大,于是我们不妨考虑线段树维护矩阵乘法。
在这里定义 \(L_i=(ch_i==B),R_i=(ch_i==B)\)
具体的,我们维护四个矩阵:
然后线段树维护下就完事了,区间翻转只需要打上相应的标记即可。
CF1368H2代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * f;
}
const int maxn = 2e5 + 10,INF = 0x3f3f3f3f;
int n, m, q;
int L[maxn], R[maxn], U[maxn], D[maxn];
char ch[maxn];
struct Matrix{
int a[2][2];
Matrix(){a[0][0] = a[0][1] = a[1][0] = a[1][1] = INF;}
friend Matrix operator * (Matrix a,Matrix b){
Matrix c;
c.a[0][0] = min(a.a[0][0] + b.a[0][0],a.a[0][1] + b.a[1][0]);
c.a[0][1] = min(a.a[0][0] + b.a[0][1],a.a[0][1] + b.a[1][1]);
c.a[1][0] = min(a.a[1][0] + b.a[0][0],a.a[1][1] + b.a[1][0]);
c.a[1][1] = min(a.a[1][0] + b.a[0][1],a.a[1][1] + b.a[1][1]);
return c;
}
};
struct ansmtx{
Matrix mtx[2][2];
ansmtx(int x){
mtx[0][0].a[0][0] = 2; mtx[0][0].a[0][1] = x;
mtx[0][0].a[1][0] = x + 2;mtx[0][0].a[1][1] = 0;
mtx[1][0].a[0][0] = 1; mtx[1][0].a[0][1] = x + 1;
mtx[1][0].a[1][0] = x + 1;mtx[1][0].a[1][1] = 1;
mtx[0][1].a[0][0] = 1; mtx[0][1].a[0][1] = x + 1;
mtx[0][1].a[1][0] = x + 1;mtx[0][1].a[1][1] = 1;
mtx[1][1].a[0][0] = 0; mtx[1][1].a[0][1] = x + 2;
mtx[1][1].a[1][0] = x; mtx[1][1].a[1][1] = 2;
}
friend ansmtx merg(ansmtx a,ansmtx b,int la,int ra,int lb,int rb){
ansmtx c = ansmtx(0);
c.mtx[0][0] = a.mtx[la ^ 0][ra ^ 0] * b.mtx[lb ^ 0][rb ^ 0];
c.mtx[0][1] = a.mtx[la ^ 0][ra ^ 1] * b.mtx[lb ^ 0][rb ^ 1];
c.mtx[1][0] = a.mtx[la ^ 1][ra ^ 0] * b.mtx[lb ^ 1][rb ^ 0];
c.mtx[1][1] = a.mtx[la ^ 1][ra ^ 1] * b.mtx[lb ^ 1][rb ^ 1];
return c;
}
};
struct Segment_Tree{
int tot;bool opt;//opt = 0 : f[i]i\in[1,n];OW:i\in[1,m]
bool leaf[maxn << 2];
struct node{
ansmtx val;bool lz, rz;int suml, sumr, l, r;
node(bool lz = 0,bool rz = 0,int l = 0,int r = 0,int suml = 0,int sumr = 0,ansmtx val = ansmtx(0)
):val(val),lz(lz),rz(rz),suml(suml),sumr(sumr),l(l),r(r){}
}d[maxn << 2];
node mergenode(node l,node r){return node(0,0,l.l,r.r,
l.suml + r.suml,l.sumr + r.sumr,merg(l.val,r.val,l.lz,l.rz,r.lz,r.rz));}
void pushdown(int p){
if(leaf[p])return;
if(d[p].lz){
d[p << 1].lz ^= 1;d[p << 1 | 1].lz ^= 1;
d[p << 1].suml = d[p << 1].r - d[p << 1].l + 1 - d[p << 1].suml;
d[p << 1 | 1].suml = d[p << 1 | 1].r - d[p << 1 | 1].l + 1 - d[p << 1 | 1].suml;
}
if(d[p].rz){
d[p << 1].rz ^= 1;d[p << 1 | 1].rz ^= 1;
d[p << 1].sumr = d[p << 1].r - d[p << 1].l + 1 - d[p << 1].sumr;
d[p << 1 | 1].sumr = d[p << 1 | 1].r - d[p << 1 | 1].l + 1 - d[p << 1 | 1].sumr;
}
d[p] = mergenode(d[p << 1],d[p << 1 | 1]);
}
void build(int l,int r,int p){
if(l == r){
leaf[p] = 1;
if(!opt){
d[p].lz = L[l];d[p].rz = R[l]; d[p].l = d[p].r = l;
d[p].suml = L[l];d[p].sumr = R[l]; d[p].val = ansmtx(m);
}
else{
d[p].lz = U[l];d[p].rz = D[l]; d[p].l = d[p].r = l;
d[p].suml = U[l];d[p].sumr = D[l]; d[p].val = ansmtx(n);
}
return;
}
int mid = l + r >> 1;
build(l,mid,p << 1);build(mid + 1,r,p << 1 | 1);
d[p] = mergenode(d[p << 1],d[p << 1 | 1]);
}
void build(int x,bool o){opt = o;tot = x;build(1,tot,1);}
void update(int l,int r,int s,int t,int p,bool op){//op=0<=>L or U;OW: R or D
if(s <= l && r <= t){
if(!op){
d[p].suml = d[p].r - d[p].l + 1 - d[p].suml;
d[p].lz ^= 1; return;
}
else {
d[p].sumr = d[p].r - d[p].l + 1 - d[p].sumr;
d[p].rz ^= 1; return;
}
}
int mid = l + r >> 1;pushdown(p);
if(s <= mid)update(l,mid,s,t,p << 1,op);
if(mid < t)update(mid + 1,r,s,t,p << 1 | 1,op);
d[p] = mergenode(d[p << 1],d[p << 1 | 1]);
}
void update(int s,int t,int op){update(1,tot,s,t,1,op);}
node query(){pushdown(1);return d[1];}
void DEBUG(int l,int r,int p){
printf("l = %d, r = %d, p = %d,suml = %d,sumr = %d\n",d[p].l,d[p].r,p,d[p].suml,d[p].sumr);
if(l == r)return; int mid = l + r >> 1;
DEBUG(l,mid,p << 1);DEBUG(mid + 1,r,p << 1 | 1);
}
void DEBUG(){DEBUG(1,tot,1);}
}tree[2];
int getans(){
// printf("tree0 : \n");tree[0].DEBUG();
// printf("tree1 : \n");tree[1].DEBUG();
Segment_Tree::node tmp0 = tree[0].query(),tmp1 = tree[1].query();
Matrix a, b;
a.a[0][0] = tmp1.suml;a.a[0][1] = m - tmp1.suml;
a.a[1][0] = a.a[1][1] = INF;
b.a[0][0] = tmp0.suml;b.a[0][1] = n - tmp0.suml;
b.a[1][0] = b.a[1][1] = INF;
a = a * tmp0.val.mtx[1 ^ tmp0.lz][1 ^ tmp0.rz];
b = b * tmp1.val.mtx[1 ^ tmp1.lz][1 ^ tmp1.rz];
// printf("n = %d:suml = %d sumr = %d, l = %d, r = %d\n",n,tmp0.suml,tmp0.sumr,tmp0.l,tmp0.r);
// printf("m = %d:suml = %d sumr = %d, l = %d, r = %d\n",m,tmp1.suml,tmp1.sumr,tmp1.l,tmp1.r);
a.a[0][0] += tmp1.sumr;a.a[0][1] += m - tmp1.sumr;
b.a[0][0] += tmp0.sumr;b.a[0][1] += n - tmp0.sumr;
return min(min(a.a[0][0],a.a[0][1]),min(b.a[0][0],b.a[0][1]));
}
signed main(){
n = read(); m = read(); q = read();
scanf("%s",ch + 1);for(int i = 1;i <= n;i++)L[i] = (ch[i] == 'B');
scanf("%s",ch + 1);for(int i = 1;i <= n;i++)R[i] = (ch[i] == 'B');
scanf("%s",ch + 1);for(int i = 1;i <= m;i++)U[i] = (ch[i] == 'B');
scanf("%s",ch + 1);for(int i = 1;i <= m;i++)D[i] = (ch[i] == 'B');
tree[0].build(n,0);tree[1].build(m,1);int u, v;
printf("%d\n",getans());
for(int i = 1;i <= q;i++){
scanf("%s%d%d",ch,&u,&v);
if(ch[0] == 'L'){tree[0].update(u, v, 0);}
if(ch[0] == 'R'){tree[0].update(u, v, 1);}
if(ch[0] == 'U'){tree[1].update(u, v, 0);}
if(ch[0] == 'D'){tree[1].update(u, v, 1);}
printf("%d\n",getans());
}
return 0;
}
/*
1 1 19
R
R
R
B
L 1 1
R 1 1
L 1 1
D 1 1
U 1 1
L 1 1
R 1 1
R 1 1
D 1 1
D 1 1
L 1 1
D 1 1
L 1 1
R 1 1
R 1 1
U 1 1
D 1 1
L 1 1
U 1 1
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号