CF249题解

CF249

Codeforces Round 152 (Div. 1)

CF249A

link

CF249A题意

在平面直角坐标系上有一个半径为 \(r\)，圆心坐标为 \((x_b,y_b)\) 的球，直线 \(y=y_w\) 为一面墙。
在 \(y\) 轴上有一个 \([y_1,y_2]\) 的球门，\((0,y_1),(0,y_2)\) 是球门的两个立柱。
现在你希望寻找一个角度，使得这个球在墙上反弹且仅反弹一次并在不触碰 \(y\) 轴上 \([0,y_1],[y_2,y_w]\)位置的前提下将球射进门，我们认为球的圆心在 \((a,b)\) 时触碰到一个点 \((x,y)\) 当且仅当 \(\sqrt{(x-a)^2+(y-b)^2}\le r\)。
你只需要输出球与墙反弹时圆心的横坐标 \(x_w\) 即可，如果有多个解输出任意一个，误差不允许超过 \(10^{-8}\)，无解输出 \(-1\)。\

CF249A题解

纯纯数学平面几何题，与OI基本没什么关系。
看这篇题解之前请确保你已经完全读懂题意。
看下面这张图（做的不好勿喷）。

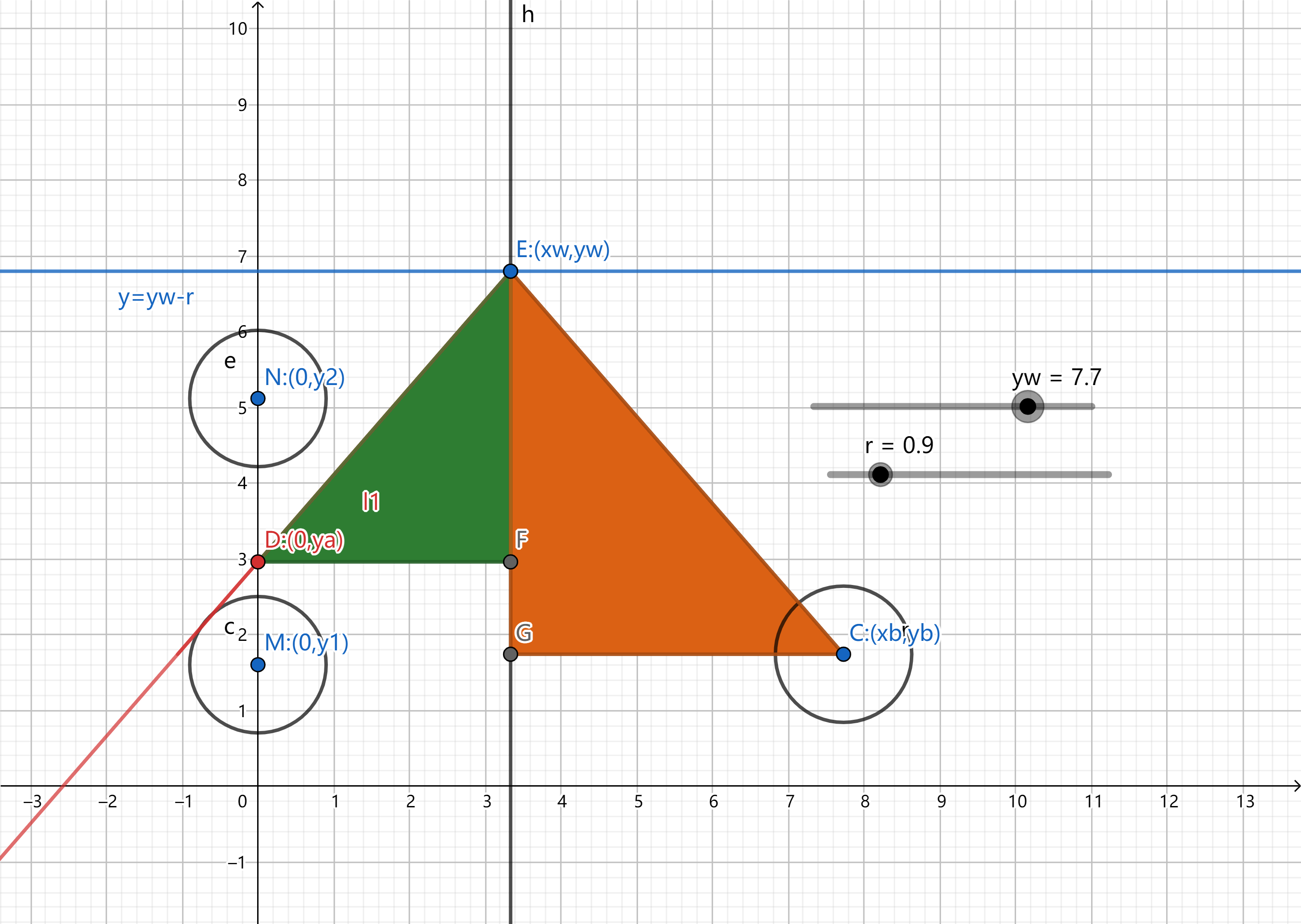
数学常用手段，希望这个圆不与 \((0,y_1),(0,y_2)\) 相碰撞（设 \(M:(0,y_1),N:(0,y_2)\)），那么就以这两个点分别做一个半径相等的圆，同时将 \(y_w\gets y_w-r\)，这样一个圆的移动就转化成了一个点的移动。
不难发现，如果希望存在一个路径满足条件，需要对于直线 \(l_1:(y_w-y_a)x-x_wy+y_ax_w=0\)，有 \(\forall A\in l_1,MA>r,NA>r\)。
不难发现，让 \(MA>r\) 是很好办的，直接让 \(y_a=y_1+r\) 即可。
然后看绿色和橙色的三角形，是不是有 \(\triangle DEF\sim\triangle CEG\)。
然后就有 $$\frac{EF}{DF}=\frac{EG}{GC}$$

\[\iff\frac{y_w-y_1-2\times r}{x_w}=\frac{y_w-y_b-r}{x_b-x_w} \]

\[\iff x_w=x_b\times\frac{y_w-y_1-2\times r}{2\times y_w-y_1-y_b-3\times r} \]

这个时候，\(D:(0,y_a),E:(x_w,y_w)\) 都已经已知，可以算出直线 \(DE\) 的解析式，即上文提到的 \(l_1\)。
接下来，根据点到直线距离公式，有

\[d=\frac{|-x_w\times y_2+y_a\times x_w|}{\sqrt{(y_w-y_a)^2+{x_w}^2}} \]

算出 \(N\) 到 \(l_1\) 的距离是 \(d\)。
然后只需要比一下 \(d\) 与 \(r\) 的关系即可，如果大于则有解，否则无解。

CF249A代码

#include<bits/stdc++.h>
using namespace std;
double y1, y2, yw, xb, yb, r, xw;
signed main(){
    scanf("%lf%lf%lf%lf%lf%lf",&y1,&y2,&yw,&xb,&yb,&r);
    double a = yw - y1 - 2.0 * r,b = yw - yb - r,x = a * xb / (a + b),l = sqrt(x * x + a * a),ans =x * (y2 - y1 - r) / l;
    if(r > ans)puts("-1");
    else printf("%.10lf\n",x);
    return 0;
}

CF249D

link

CF249D题意

坐标系上给出 \(n\) 个点。

求最多有多少个点依次连成的折线上的线段的斜率在 \(\frac{a}{b}\) 到 \(\frac{c}{d}\) 之间。

第一条折线的起点必须从坐标原点开始且坐标原点不计入答案。

CF249D题解

平面几何+线段树优化DP。
发现有斜率限制不太好做，考虑转化。
因为上面给出 \(\frac{a}{b}\neq\frac{c}{d}\)，故向量 \(\vec{a}=(b,a),\vec{b}=(d,c)\) 就是这个平面的一组基向量。
不难发现，如果设行进方向向量 \(\vec{vec_i}\)，那么一定能够得到 \(u_i\times\vec{a}+v_i\times\vec{b}=vec_i\)。
发现，如果这个行进向量是合法的，那么一定有 \(u_i>0,v_i>0\)。
于是尝试让所有的点用 \((u_i,v_i)\) 来表示，其中 \(u_i\times\vec{a}+v_i\times\vec{b}=(x_i,y_i)\)。
现在如果想从 \(i\to j\)，就需要 \(u_j>u_i\) 且 \(v_j>v_i\)。
发现这玩应就是LIS，只不过是二元的。
首先发现我们关心的是 \(u_i,v_i\) 的大小关系，故先进行离散化。
然后建一棵线段树，位置 \(i\) 存储 \(v_j=i\)为结尾时的LIS。
然后就有 \(f_i=1+\max_{j=1}^{v_j-1}f_j\)。
然后就做完了。

CF249D代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read(){
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}
const int maxn = 1e5 + 10;
int n;
int a, b, c, d;
ll x[maxn], y[maxn];
ll u[maxn], v[maxn];
pair<int,int> s[maxn];

struct Segment_Tree{
    int tot;
    struct node{
        int maxx;
        node(int maxx = 0):maxx(maxx){}
    }d[maxn << 2];
    node mergenode(node l,node r){return node(max(l.maxx,r.maxx));}
    void build(int l,int r,int p){
        if(l == r){d[p] = node();return;}
        int mid = l + r >> 1;
        build(l,mid,p << 1);build(mid + 1,r,p << 1 | 1);
    }
    void update(int l,int r,int pos,int p,int upd){
        if(l == r && l == pos){d[p].maxx = max(upd,d[p].maxx);return;}
        int mid = l + r >> 1;
        if(pos <= mid)update(l,mid,pos,p << 1,upd);
        else update(mid + 1,r,pos,p << 1 | 1,upd);
        d[p] = mergenode(d[p << 1],d[p << 1 | 1]);
    }
    node query(int l,int r,int s,int t,int p){
        if(s <= l && r <= t)return d[p];
        int mid = l + r >> 1;
        if(t <= mid)return query(l,mid,s,t,p << 1);
        if(mid < s)return query(mid + 1,r,s,t,p << 1 | 1);
        return mergenode(query(l,mid,s,t,p << 1),query(mid + 1,r,s,t,p << 1 | 1));
    }
    void build(int x){tot = x;build(1,tot,1);}
    void update(int pos,int upd){update(1,tot,pos,1,upd);}
    int query(int s,int t){if(s > t)return 0;return query(1,tot,s,t,1).maxx;}
}tree;

signed main(){
    n = read();scanf("%d/%d",&b,&a); scanf("%d/%d",&d,&c);
    for(int i = 1;i <= n;i++){
        x[i] = read(); y[i] = read();
        u[i] = -(ll)y[i] * c + x[i] * d;
        v[i] = -(ll)x[i] * b + y[i] * a;
        if(u[i] < 0 || v[i] < 0){n--;i--;continue;}
        // printf("i = %d, u = %lld, v = %lld\n",i,x[i],y[i]);
        x[i] = u[i]; y[i] = v[i];
    }
    if(n == 0){puts("0");return 0;}
    // printf("n = %d\n", n);
    sort(x + 1,x + 1 + n);int totx = unique(x + 1,x + 1 + n) - x - 1;
    sort(y + 1,y + 1 + n);int toty = unique(y + 1,y + 1 + n) - y - 1;
    for(int i = 1;i <= n;i++){
        u[i] = lower_bound(x + 1,x + 1 + totx,u[i]) - x;
        v[i] = lower_bound(y + 1,y + 1 + toty,v[i]) - y;
        s[i] = make_pair(u[i],v[i]);
        // printf("i = %d, u = %d, v = %d\n",i,s[i].first,s[i].second);
    }
    sort(s + 1,s + 1 + n,[](pair<int,int> a,pair<int,int> b)
    {return a.first != b.first ? a.first < b.first : a.second > b.second;});
    tree.build(toty);int ans = 0;
// puts("1111111");
    for(int i = 1;i <= n;i++){
        int cnt = 1 + tree.query(1,s[i].second - 1);
        ans = max(ans,cnt);
        tree.update(s[i].second,cnt);
    }
    printf("%d\n",ans);
    return 0;
}

CF249E

link

CF249E题意

给你一个形如下图的矩阵

并有 \(T\) 组询问 每组询问给出 \(x_1,y_1,x_2,y_2\)。

求 \(\sum_{i=x_1}^{x_2}\sum_{j=y_1}^{y_2}A[i][j]\)。

其中 \(A[i][j]\) 表示在矩阵中的数。

\(T\leq 10^5\)
\(1\leq x_1 \leq x_2 \leq 10^9\)
\(1\leq y_1 \leq y_2 \leq 10^9\)

CF249E题解

首先先将询问拆成 \((x_2,y_2)-(x_1-1,y_2)-(x_2,y_1-1)+(x_1-1,y_1-1)\)。
然后现在考虑怎么求 \((1,1)\to (x,y)\) 的总和。
首先知道一个结论，就是 \((1,y)=((y-1)^2+1),(x,1)=x^2\)。
设 \(n=\min(x,y)\)，现在知道了 \((1,1)\to(n,n)\) 的答案是 \(\frac{n^2\times(n^2+1)}{2}\)。
这里不妨设 \(sum(n)=\sum_{i=1}^n,squ(n)=\sum_{i=1}^ni^2\)。
然后分类讨论剩下的：

• \(x>y\)，观察图形，可知每一行都是从最左侧开始递减，每次递减一。
  • 先算递减一的代价，每一行的递减总和是 \(sum(y-1)\)，一共 \(x-y\) 行，所以对答案的贡献是 \(-sum(y-1)\times (x-y)\)。
  • 然后算剩下的，每一列的答案都是 \(squ(x)-squ(y)\)，总和就是 \((squ(x) -squ(y))\times y\)。
• \(x<y\)，同样观察图形，可知每一列都是从最上面开始递增，每次递增一。
  • 先算递增一的贡献，每一列的递增总和是 \(sum(y)\)，一共 \(y-x\) 行，所以对答案的贡献是 \(sum(y)\times (y-x)\)。
  • 然后算剩下的，每一行的答案都是 \(squ(y - 1) - squ(x - 1)\)，总和就是 \((squ(y - 1) -squ(x-1))\times x\)

哦对了中间的答案最大不会超过 \(n^4\)，__int128可以驾驭，但long long好像不太行。
大水题快来切啊（bushi）

CF249E代码

#include<bits/stdc++.h>
#ifndef ONLINE_JUDGE
#define __int128 long long
#endif
#define i128 __int128
#define ll long long
using namespace std;
inline ll read(){
    ll x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9'){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * f;
}

inline i128 summ(i128 x){return (x + 1) * x / 2;}
inline i128 squu(i128 x){return x * (x + 1) * (2 * x + 1) / 6;}

i128 solve(i128 x,i128 y){
    if(x <= 0 || y <= 0)return 0;
    i128 n = min(x, y);
    i128 ans = summ(n * n);
    if(x > y){
        ans -= (x - y) * summ(y - 1);
        ans += (squu(x) - squu(y)) * y;
    }
    else if(x < y){
        ans += (y - x) * summ(x);
        ans += (squu(y - 1) - squu(x - 1)) * x;
    }
    return ans;
}

signed main(){
int T = read();
while(T--){
    ll xl = read(), yl = read(), xr = read(), yr = read();
    i128 ans = solve(xr,yr) - solve(xl - 1,yr) - solve(xr,yl - 1) + solve(xl - 1,yl - 1);
    if(ans > (i128)1e10){ans = ans % (i128)1e10;printf("...%010lld\n",(ll)ans);}
    else printf("%lld\n",(ll)ans);
}
    // printf("%lld\n",(ll)solve(1,3));
    return 0;
}