网络流杂题+不多的归纳

照着ppt写博客的时代应是一去不复返了，借不同题目阐述基本思想当为至道。
转个链接：https://www.cnblogs.com/SYCstudio/p/7260613.html ，这篇笔记写得很好。
引入题目之前，阐明一些想法。

首先，在网络流中最重要的就是建图，有了图，基本就能解决问题了。将这个过程模式化一下，便会有不同的建图思想/方法，这是我们应该重点探寻的。

公平分配类

UVA1306 The-K-League

题意：

有 \(n\) 支队伍进行比赛，每支队伍需要打的比赛数目相同。每场比赛恰好一支队伍胜，另一支败。给出每支队伍目前胜的场数和败的场数，以及每两个队伍还剩下的比赛场数，确定所有可能得冠军的球队（获胜场数最多的得冠军，可以并列）。

令 \(w[i]\) 为第 \(i\) 支队伍已赢过的场数，\(d[i]\) 为第 \(i\) 支队伍已输过的场数，\(a[i][j]\) 为第 \(i\) 支队伍和第 \(j\) 支队伍还剩的比赛场数。

要想要一个队伍获胜，就需要让它的获胜场数成为所有队伍中最多的。根据题目中给出的信息，我们能够确定每个队伍的最大获胜场数，即假定它剩下的场数全赢，并加上其之前获胜的场数，记这个数字为 \(maxwin[i] = w[i] + \sum_j^{n}a[i][j]\)。

钦定 \(i\) 为冠军，那么队伍 \(j\) 在剩下的场数中最多能赢的数量就为 \(max(0,maxwin[i] - w[j])\)，否则的话，就会有队总共赢的场数大于 \(i\) 队伍，使假设不成立。

如此，问题就转化为一个分配问题：在 \(a\) 与 \(b\) 的比赛中，\(a\) 赢的场数为 \(x\)，\(b\) 赢的场数为 \(y\)，\(x + y = a[i][j]\)，如何分配 \(x\) 和 \(y\) 能满足题设。

在网络流中，诸如这种分配问题，常建一个点，源点到这个点有一条边，最大容量为你希望分配下去的值。这个题目中，分配的值即为 \(a[i][j]\)，它分配的对象为 \(i\) \(j\) 两个点。

显然，我们可以对 \(u\) 和 \(v\) 之间的比赛 \((u,v)\) 建一个点，从源点向这个点连一条最大容量为 \(a[u][v]\) 的点，再从这个点向 \(u\) 和 \(v\) 各连一条容量无穷大的点。再从 \(u\) 向汇点连一条容量为 \(max(0,maxwin[i] - w[u])\) 的边，从 \(v\) 向汇点连一条 \(max(0,maxwin[i] - w[v])\) 的边。如此反复进行。

源点向其他点的边的最大容量限定了分配总数量，点向汇点的边限定了每个单位被分配的最大值。

每次枚举一个 \(i\)，钦定它为冠军，按上面的方法建一个图，跑一次最大流。如果图满流，说明所有可供分配的比赛都分配下去了，则 \(i\) 可能为冠军；如果不能满流，就说明在分配过程中出了冲突，\(i\) 不能为冠军。

点击查看代码

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int MAXN = 2e3;
const int INF = 0x7fffffff;
int n,T,total,head[MAXN + 5],tot = 1,w[MAXN + 5],d[MAXN + 5],a[MAXN + 5][MAXN + 5],s,t,dep[MAXN + 5],cur[MAXN + 5];
struct EDGE{
	int u,v,c,next;
}edge[MAXN + 5];
void ADD(int u,int v,int ww){
	++tot;
	edge[tot].u = u;
	edge[tot].v = v;
	edge[tot].c = ww;
	edge[tot].next = head[u];
	head[u] = tot;
}
void add(int u,int v,int ww){
	ADD(u,v,ww);
	ADD(v,u,0);
}
bool check(int u){
	for(int i = 1; i <= n; i++){
		if(w[i] > total - d[u])return 0;
	}
	return 1;
}
inline bool bfs(){
    queue<int>q;
    q.push(s);
    memset(dep,0,sizeof(dep));
    cur[s] = head[s];
    dep[s] = 1;
    while(!q.empty()){
        int x = q.front();
        q.pop();
        for(int i = head[x]; i; i = edge[i].next){
            int y = edge[i].v;
            if(dep[y] || !edge[i].c){
                continue;
            }
            dep[y] = dep[x]+1;
            cur[y] = head[y];
            q.push(y);
            if(y == t){
                return 1;
            }
        }
    }
    return 0;
}
inline int dfs(int x,int flow){
    if(x == t || !flow){
        return flow;
    }
    int limit,res=0;
    for(int i = cur[x]; i && flow;i=edge[i].next){
        cur[x] = i;
        int y = edge[i].v;
        if(dep[y] == dep[x] + 1 && edge[i].c){
            limit = dfs(y,min(flow,edge[i].c));
            if(!limit){
                dep[y] = 0;
            }
			else{
                edge[i].c -= limit;
                edge[i^1].c += limit;
                res += limit;
                flow -= limit;
            }
        }
    }
    return res;
}
inline int dinic(){
    int res = 0;
    while(bfs()){
        res += dfs(s,INF);
    }
    return res;
}
int main(){
	t = 1500;
	scanf("%d",&T);
	while(T--){
		total = 0,tot = 1;
		scanf("%d",&n);
		int sum = 0;
		for(int i = 1; i <= n; i++){
			scanf("%d%d",&w[i],&d[i]);
		}
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= n; j++){
				scanf("%d",&a[i][j]);
				sum += a[i][j];
			}
		}
		sum /= 2;
		for(int i = 1; i <= n; i++)total += a[1][i];
		total += w[1] + d[1];
		bool flag = 0;
		for(int i = 1; i <= n; i++){
			if(!check(i))continue;
			memset(head,0,sizeof head);
			memset(edge,0,sizeof edge);
			tot = 1;
			int num = 0;
			for(int j = 1; j <= n; j++){
				for(int k = j + 1; k <= n; k++){
					if(a[j][k]){
						add(++num,j + 1000,a[j][k]);
						add(num,k + 1000,a[j][k]);
						add(s,num,a[j][k]);
					}
				}
			}
			for(int j = 1; j <= n; j++){
				add(j + 1000,t,total - d[i] - w[j]);
			}
			if(dinic() == sum){
				if(!flag)cout << i;
				else cout << " " << i;
				flag = 1;
			}
		}
		puts("");
	}	
}

转移问题

这种问题一般涉及到人、物在地点之间的转移，同时两地之间的转移数量有一个上限，也可能有时间限制。

UVA10983 Buy one,Get the rest free

有 \(N\) 个城市，每个城市都有一些选手要到第 \(N\) 个城市去参加比赛。比赛的组织者可以租用城市之间的一些飞机，他们的出发时间可能不同，但是都是从某天晚上出发，然后第二天早上到大目的地，每架飞机上都有载客上限和租金。现在有一个优惠：只要租用一架飞机，就可以免费使用所有价格小于等于该租金的飞机。组织者希望在 \(d\) 天内花最少的钱把所有的选手送到比赛地。
比如说，有 \(4\) 架飞机，租金分别是 \(10000\)，\(25000\)，\(30000\)，\(40000\)，你租下 \(30000\) 元的那架，那么就可以免费使用 \(10000\) 和 \(25000\) 的那架。相当于租下3架飞机的费用就是\(30000\)。

题目中出现了天数的限制，从第 \(0\) 天到第 \(d\) 天，每个城市有不同的状态，不妨把每个城市拆成 \(d + 1\) 个点（这种根据状态拆点的思想在今后很常用），每个点表示当前城市在这天的情况。每个城市不同状态的点两两间连容量为正无穷的边，表示旅客可以停留在当前城市，以第 \(n\) 个城市第 \(d\) 天的状态为汇点。自然，从起点向每个城市第 \(0\) 天状态连的边的最大容量应为这个城市第 \(0\) 的人数。

而航班，在这个题目中承担着沟通不同状态城市的任务。因此把航班作为边。对于一个 第 \(e\) 天从 \(u\) 出发，第 \(e + 1\) 天到达 \(v\)，载客量为 \(c\) 的航班，不妨将它作为从 \(u\) 的第 \(e\) 天状态连向 \(v\) 的第 \(e + 1\) 个状态，最大容量为 \(c\) 的边。

然后将航班按照价格从小到大排序，每次二分一个航班编号，将价格小于等于它的航班按上面的标准在图上连边，跑一边最大流，如果最大流等于所有旅客数量，则合法。

点击查看代码

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int MAXN = 350;
int T,n,m,d,tot,head[MAXN + 5],dis[MAXN + 5],node[50][20],cnt,z[MAXN + 5],hum,cntt,s,t,cur[MAXN + 5];
struct EDGE{
	int u,v,w,next;
}edge[400005];
struct PLA{
	int u,v,c,p,e;
	bool operator<(const PLA a)const{
		return this->p < a.p;
	}
}pla[400000 + 5];
void add(int u,int v,int w){
	++tot;
	edge[tot].u = u;
	edge[tot].v = v;
	edge[tot].next = head[u];
	edge[tot].w = w;
	head[u] = tot;
	++tot;
	edge[tot].u = v;
	edge[tot].v = u;
	edge[tot].next = head[v];
	edge[tot].w = 0;
	head[v] = tot;
}
bool bfs(){
	queue<int> q;
	memset(dis,0,sizeof dis);
	q.push(s);
	dis[s] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		for(int i = head[u]; i; i = edge[i].next){
			int v = edge[i].v;
			if(!dis[v] && edge[i].w > 0){
				q.push(v);
				dis[v] = dis[u] + 1;
			}
		}
	}
	if(dis[t])return 1;
	return 0;
}	
int dfs(int u,int dist){
	if(u == t)return dist;
	for(int &i = cur[u]; i; i = edge[i].next){
		int v = edge[i].v;
		if(dis[v] == dis[u] + 1 && edge[i].w > 0){
			int di = dfs(v,min(dist,edge[i].w));
			if(di > 0){
				edge[i].w -= di;
				edge[i ^ 1].w += di;
				return di;
			}
		}
	}
	return 0;
}
int dinic(){
	int ans = 0;
	while(bfs()){
		for(int i = 0; i <= cnt; i++)cur[i] = head[i];
		while(int di = dfs(s,1000000000))ans += di;
	}
	return ans;
}
void build(int u){
	memset(head,0,sizeof head);
	memset(edge,0,sizeof edge);
	tot = 1;
	for(int i = 1; i <= n; i++){
		add(s,node[i][0],z[i]);
	}
	for(int i = 1; i <= n; i++){
		for(int j = 0; j < d; j++){
			add(node[i][j],node[i][j + 1],1000000000);
		}
	}
	for(int i = 1; pla[i].p <= pla[u].p && i <= m; i++){
		add(node[pla[i].u][pla[i].e],node[pla[i].v][pla[i].e + 1],pla[i].c);
	}
}
bool check(int u){
	build(u);
	int k = dinic();
	if(k >= hum)return 1;
	return 0;
}
signed main(){
	scanf("%d",&T);
	while(T--){
		cnt = hum = 0;
		memset(pla,0,sizeof pla);
		scanf("%d%d%d",&n,&d,&m);
		for(int i = 1; i <= m; i++){
			scanf("%d%d%d%d%d",&pla[i].u,&pla[i].v,&pla[i].c,&pla[i].p,&pla[i].e);
		}
		for(int i = 1; i <= n; i++){
			for(int j = 0; j <= d; j++)node[i][j] = ++cnt;
		}
		for(int i = 1; i <= n; i++)scanf("%d",&z[i]),hum += z[i];
		s = 0,t = node[n][d];
		sort(pla + 1,pla + 1 + m);
		int l = 0,r = m + 1;
		bool flag = 0;
		if(z[n] == hum){
			printf("Case #%d: 0\n",++cntt);
			continue;
		}
		while(l + 1 < r){
			int mid = (l + r) / 2;
			PLA p = pla[mid];
			if(check(mid))r = mid,flag = 1;
			else l = mid;
		}
		if(flag)printf("Case #%d: %d\n",++cntt,pla[r].p);
		else printf("Case #%d: Impossible\n",++cntt);
	}
}

UVA12125 March of the Penguins

题目描述
给定 \(n\) 块冰的坐标和企鹅能跳的距离 \(d\)，每块冰有 \(4\) 个属性，分别为 \(x\) 坐标，\(y\) 坐标，上面原有的企鹅的数量 \(m\) 和最多能跳出多少次 \(k\)，求哪些冰块可以让所有企鹅都跳到上面。
输入格式
第一行一个正整数 \(T\)，代表数据组数；
对于每组数据，第一行一个整数 \(n\) 和一个浮点数 \(d\)，代表冰块总数和企鹅能跳多远；
后 \(n\) 行，每行有 \(4\) 个整数，分别为冰块的坐标、原本冰块上有几只企鹅、每块冰最多能跳出多少次。
输出格式
对于每组数据，输出若干个数，为能让所有企鹅跳到上面的冰块的序号，如果没有一块冰符合条件，输出 \(-1\)。

类似于上题，对于距离小于等于 \(d\) 的两块冰块 \(a\) \(b\)，从 \(a\) 向 \(b\) 连一个最大容量为 \(k[a]\) 的边，从 \(b\) 向 \(a\) 连一个最大容量为 \(k[b]\) 的边。从汇点向每块冰连一个 最大容量 \(m[i]\) 的边。枚举每一块冰作为汇点，跑最大流，如果最大流等于企鹅数则可行。

点击查看代码

#include<iostream>
#include<queue>
#include<cmath>
#include<cstring>
using namespace std;
const int MAXN = 1e5;
int T,n,tot,head[1000 + 5],dis[1000 + 5],cur[1000 + 5],pen,s,t,cnt;
pair<int,int> divv[1000 + 5];
double d;
struct EDGE{
	int u,v,c,next;
}edge[MAXN + 5];
struct ICE{
	int x,y,n,m;
}ice[1000 + 5];
double get(int x1,int y1,int x2,int y2){
	return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
void add(int u,int v,int w){
	edge[++tot].next = head[u];
	edge[tot].u = u;
	edge[tot].v = v;
	edge[tot].c = w;
	head[u] = tot;
}
void build(int u){
	memset(head,0,sizeof head);
	memset(edge,0,sizeof edge);
	tot = 1;
	for(int i = 1; i <= n; i++){
		if(i == u)continue;
		add(s,divv[i].first,ice[i].n);
		add(divv[i].first,s,0);
		add(divv[i].first,divv[i].second,ice[i].m);
		add(divv[i].second,divv[i].first,0);
	}
	for(int i = 1; i <= n; i++){
		if(i == u)continue;
		for(int j = i + 1; j <= n; j++){
			double di = get(ice[i].x,ice[i].y,ice[j].x,ice[j].y);
			if(di > d)continue;
			add(divv[i].second,divv[j].first,1000000000);
			add(divv[j].first,divv[i].second,0);
			add(divv[j].second,divv[i].first,1000000000);
			add(divv[i].first,divv[j].second,0);
		}
		double di = get(ice[i].x,ice[i].y,ice[u].x,ice[u].y);
		if(di > d)continue;
		add(divv[i].second,t,ice[i].m);
		add(t,divv[i].second,0);
	}
}
bool bfs(){
	queue<int> q;
	q.push(s);
	memset(dis,0,sizeof dis);
	dis[s] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		for(int i = head[u]; i; i = edge[i].next){
			int v = edge[i].v;
			if(!dis[v] && edge[i].c){
				dis[v] = dis[u] + 1;
				q.push(v);
			}
		}
	}
	if(dis[t])return 1;
	return 0;
}
int dfs(int u,int dist){
	if(u == t)return dist;
	for(int &i = cur[u]; i; i = edge[i].next){
		int v = edge[i].v;
		if(dis[v] == dis[u] + 1 && edge[i].c > 0){
			int di = dfs(v,min(dist,edge[i].c));
			if(di > 0){
				edge[i].c -= di;
				edge[i ^ 1].c += di;
				return di;
			}
		}
	}
	return 0;
}
int dinic(){
	int ans = 0;
	while(bfs()){
		for(int i = 0; i <= cnt; i++)cur[i] = head[i];
		while(int di = dfs(s,1000000000))ans += di;
	}
	return ans;
}
int main(){
	scanf("%d",&T);
	while(T--){
		cnt = pen = 0; 
		memset(divv,0,sizeof divv);
		scanf("%d%lf",&n,&d);
		for(int i = 1; i <= n ; i++){
			scanf("%d%d%d%d",&ice[i].x,&ice[i].y,&ice[i].n,&ice[i].m);
			pen += ice[i].n;
			divv[i] = make_pair(++cnt,++cnt);
		}
		s = 0,t = ++cnt;
		bool flag = 0;
		int f = 0;
		for(int i = 1; i <= n; i++){
			build(i);
			int k = dinic();
			if(k == pen - ice[i].n){
				flag = 1;
				if(!f)cout << i - 1;
				else cout << " " << i - 1;
				f = 1;
			}
			
		}
		if(!flag)cout << "-1";
		puts("");
	}
}

最大流最小割定理的应用

POJ3469：Dual Core CPU

给 \(n\) 个模块，每个模块在 \(A\) 核花费为 \(a_i\)，在 \(B\) 核跑花费为 \(b_i\)，然后有 \(m\) 个任务 \((u_i,v_i,w_i)\)，表示如果 \(u_i\)，\(v_i\) 不在同一个核上跑，额外的花费为 \(w_i\)，求最小的花费。

这个题用最大流似乎并不好想。

既然有两个核，也就是要将所有模块分成两部分，也就相当于割掉一些边，并求最小值，这不就相当于最小割吗？

不妨一个设为源点，一个设为汇点。从 \(A\) 出发向每个模块连最大容量为 \(a_i\) 的边，从每个模块出发向 \(B\) 连最大容量为 \(b_i\) 的边。在从给出的任务中，在 \(u_i\) 和 \(v_i\) 之间连一条最大容量为 \(w_i\) 的双向边。这样就保证了将 \(u_i\) 和 \(v_i\) 割开必须额外付出 \(w_i\) 的代价。

跑一边最大流，即可求出最小割。

点击查看代码

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int MAXN = 1e6;
int n,m,head[MAXN + 5],tot,s,t,dis[MAXN + 5],cur[MAXN + 5];
struct EDGE{
	int u,v,c,next;
}edge[3 * MAXN + 5];
void add(int u,int v,int ww){
	edge[++tot].next = head[u];
	edge[tot].u = u;
	edge[tot].v = v;
	edge[tot].c = ww;
	head[u] = tot;
}
bool bfs(){
	queue<int> q;
	q.push(s);
	memset(dis,0,sizeof dis);
	dis[s] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		for(int i = head[u]; i; i = edge[i].next){
			int v = edge[i].v;
			if(!dis[v] && edge[i].c != 0){
				q.push(v);
				dis[v] = dis[u] + 1;
			}
		}
	}
	if(!dis[t])return 0;
	return 1;
}
int dfs(int u,int dist){
	if(u == t)return dist;
	for(int &i = cur[u]; i; i = edge[i].next){
		int v = edge[i].v;
		if(dis[v] == dis[u] + 1 && edge[i].c > 0){
			int di = dfs(v,min(dist,edge[i].c));
			if(di > 0){
				edge[i].c -= di;
				edge[i ^ 1].c += di;
				return di;
			}
		}
	}
	return 0;
}
int dinic(){
	int ans = 0;
	while(bfs()){
		for(int i = 0; i <= n + 1; i++)cur[i] = head[i];
		while(int d = dfs(s,1090000000))ans += d;
	}
	return ans;
}
int main(){
	scanf("%d%d",&n,&m);
	s = 0,t = n + 1;
	tot = 1;
	for(int i = 1; i <= n; i++){
		int a,b;
		scanf("%d%d",&a,&b);
		add(s,i,a);
		add(i,s,0);
		add(i,t,b);
		add(t,i,0);
	}
	for(int i = 1; i <= m; i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
		add(v,u,0);
		add(v,u,w);
		add(u,v,0);
	}
	int ans = dinic();
	cout << ans << "\n";
}

其他类型

UVA11082 矩阵解压 Matrix Decompressing

计算出每行、每列的和，给每行、每列各自建一个点，从源点向所有行点各自连一条边，最大容量为该行元素和；从所有列点向汇点各自连一条边，最大容量为该列元素和，行点、列点两两相连，最大容量为正无穷。跑一遍最大流，记录行点与列点之间的边的流量，这就是该行与该列交点的大小。

为了使最后的结果每个数字大于等于 \(1\)，可以先假设将矩阵中每个点减一，输出时加一即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 410;
const int INF = 0x3f3f3f3f;
int T,s,t,n,m,tot,cnt,dis[50 + 5],cur[50 + 5],col[50 + 5],row[50 + 5],cntt,head[50 + 5],r[50 + 5],c[50 + 5],a[50 + 5][50 + 5];
struct EDGE{
	int u,v,w,next,f;
}edge[800 + 5];
void add(int u,int v,int w){
	++tot;
	edge[tot].next = head[u];
	edge[tot].u = u;
	edge[tot].v = v;
	edge[tot].w = w;
	head[u] = tot;
	a[u][v] = tot;
	++tot;
	edge[tot].next = head[v];
	edge[tot].u = v;
	edge[tot].v = u;
	edge[tot].w = 0;
	head[v] = tot;
	a[v][u] = tot;
}
void build(){
	memset(cur,0,sizeof cur);
	memset(edge,0,sizeof edge);
	memset(head,0,sizeof head);
	tot = 1;
	for(int i = 1; i <= n; i++){
		add(s,++cnt,row[i] - m);
		r[i] = cnt;
	}
	for(int i = 1; i <= m; i++){
		add(++cnt,t,col[i] - n);
		c[i] = cnt;
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			add(r[i],c[j],19);
		}
	}
	++cnt;
}
bool bfs(){
	queue<int> q;
	q.push(s);
	memset(dis,0,sizeof dis);
	dis[s] = 1;
	while(!q.empty()){
		int u = q.front();
		q.pop();
		for(int i = head[u]; i; i = edge[i].next){
			int v = edge[i].v;
			if(!dis[v] && edge[i].w > 0){
				dis[v] = dis[u] + 1;
				q.push(v);
			}
		}
	}
	if(dis[t])return 1;
	return 0;
}
int dfs(int u,int dist){
	if(u == t)return dist;
	for(int &i = cur[u]; i; i = edge[i].next){
		int v = edge[i].v;
		if(dis[v] == dis[u] + 1 && edge[i].w > 0){
			int di = dfs(v,min(edge[i].w,dist));
			if(di > 0){
				edge[i].w -= di;
				edge[i].f += di;
				edge[i ^ 1].w += di; 
				return di;
			}
		}
	}
	return 0;
}
int dinic(){
	int ans = 0;
	while(bfs()){
		for(int i = 0; i <= cnt; i++)cur[i] = head[i];
		while(int di = dfs(s,INF))ans += di;
	}
	return ans;
}
int main(){
	//freopen("a","w",stdout);
	scanf("%d",&T);
	while(T--){
		memset(a,0,sizeof a);
		cnt = 0;
		if(cntt != 0)puts("");
		scanf("%d%d",&n,&m);
		for(int i = 1; i <= n; i++)scanf("%d",&row[i]);
		for(int i = n; i >= 1; i--)row[i] -= row[i - 1];
		for(int i = 1; i <= m; i++)scanf("%d",&col[i]);
		for(int i = m; i >= 1; i--)col[i] -= col[i - 1];
		t = n + m + 1;
		build();
		int k;
		k = dinic();
		printf("Matrix %d\n",++cntt);
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= m; j++){
				int l = edge[a[r[i]][c[j]] ^ 1].w;
				if(j != 1)cout << " ";
				cout << l + 1;
			}
			puts("");
		}
	}	
} 

捆绑模型

捆绑类问题是网络流中常出现的问题之一。一般是做出一个选择后，要求必须做规定的另一个选择，否则将会付出无穷大的代价，并求问最小的代价为多少。这样的问题一般能转化为最小割问题。下面由简单到难看几道例题。

洛谷 P4313 文理分科

文理分科是一件很纠结的事情！（虽然看到这个题目的人肯定都没有纠
结过）
小P所在的班级要进行文理分科。他的班级可以用一个 \(n*m\) 的矩阵进行
描述，每个格子代表一个同学的座位。每位同学必须从文科和理科中选择
一科。同学们在选择科目的时候会获得一个满意值。满意值按如下的方式
得到：
1．如果第 \(i\) 行第 \(j\) 列的同学选择了文科，则他将获得 \(art[i][j]\) 的满意值，如
果选择理科，将得到 \(science[i][j]\)的满意值。
2．如果第 \(i\) 行第 \(j\) 列的同学选择了文科，并且他相邻（两个格子相邻当且
仅当它们拥有一条相同的边）的同学全部选择了文科，则他会更开
心，所以会增加 \(same-art[i][j]\)的满意值。
3．如果第 \(i\) 行第 \(j\) 列的同学选择了理科，并且他相邻的同学全部选择了理
科，则增加 \(same-science[i][j]\) 的满意值。
小P想知道，大家应该如何选择，才能使所有人的满意值之和最大。请
告诉他这个最大值。

还记得上文提到的 \(Dual\) \(CPU\) \(Core\) 那个题吗？那个题也相当于是一个捆绑——两个物品同在一个核上处理可节省 \(w[i]\) 的代价。我们可以通过新建一个点来表示两者间是否在一个核处理。这个题也是类似的——只不过捆绑关系从两个变成了四个。鉴于此，尝试新建一个点 \(a\) 表示点 \((i,j)\) 周围的点是否都选了文科。连边的时候，从源点向 \(a\) 连一条容量为 \(same-art[i][j]\) 的边，从 \(a\) 向表示 \((i,j)\)、\((i + 1,j)\)、\((i,j + 1)\)、\((i - 1,j)\)、\((i,j - 1)\) 的点各连一条容量为正无穷的边。类似的，新建一个点 \(b\) 表示该点周围的点是否都选了理科。从 \(b\) 向源点连一条容量为 \(same-science[i][j]\) 的边，由表示 \((i,j)\)、\((i + 1,j)\)、\((i,j + 1)\)、\((i - 1,j)\)、\((i,j - 1)\) 的点向 \(b\) 各连一条容量为正无穷的边。效果如下：

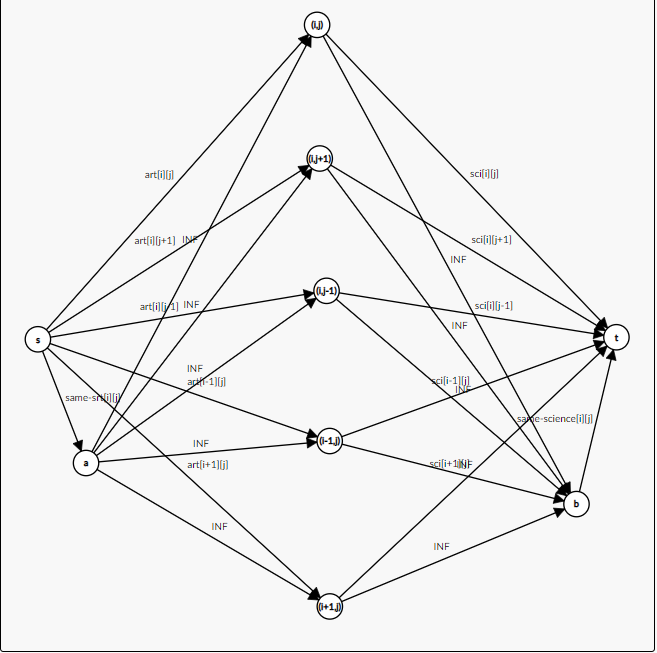
割掉其中的一条边，就相当于放弃了这条边所能带来的满意度。显然，容量为 \(INF\) 的边肯定不会出现在最小割中，这就防止出现相邻的几个同学选择的科目不同，但是能得到 \(same-art\) 或\(same-science\) 的满意度。所以最小割就相当于我们所需要付出的最小代价，用总共的满意度减去这个最小代价即可。

一个脑筋急转弯：

P1935 [国家集训队]圈地计划

最近房地产商 \(GDOI(Group of Dumbbells Or Idiots)\) 从 \(NOI(Nuts Old Idiots)\) 手中得到了一块开发土地。据了解，这块土地是一块矩形的区域，可以纵横划分为N×M块小区域。\(GDOI\) 要求将这些区域分为商业区和工业区来开发。根据不同的地形环境，每块小区域建造商业区和工业区能取得不同的经济价值。更具体点，对于第 \(i\) 行第 \(j\) 列的区域，建造商业区将得到\(A_{ij}\)收益，建造工业区将得到 \(B_{ij}\) 收益。另外不同的区域连在一起可以得到额外的收益，即如果区域 \((i,j)\) 相邻（相邻是指两个格子有公共边）有 \(K\) 块（显然 \(K\) 不超过4）类型不同于 \((i,j)\) 的区域，则这块区域能增加 \(K×C_{ij}\)收益。经过 \(Tiger.S\)教授的勘察，收益矩阵\(A\),\(B\),\(C\)都已经知道了。你能帮 \(GDOI\) 求出一个收益最大的方案么？

第一个转化：周围 \(K\) 块的区域类型与它不同能增加 \(K * c[i][j]\) 的收益，就相当于该位置的区域类型只要与相邻的一块区域不同，就可以增加一个 \(c[i][j]\)，所以只需新建一个点表示相邻两个点之间的区域类型种类是否一样即可。

第二个转化：之前做的都是两两选择相同才会有收益的捆绑问题，而这个要求的是两两选择不同。如何转化？不妨考虑黑白染色。这是一种对于相邻者的选择需要相反的问题常用的思维方式。

容易发现，白色位置的附加权值取决于相邻的四个黑色位置。假设白色的是工业区，那黑色块的只有是商业区才能带来附加权值。那么不妨交换黑色块 \(A\) 和 \(B\) 的值，这样两个位置本来要选择不一样才会有附加权值，现在变成了两个位置集合相同才会有附加权值。剩下的就不必说了。

这种取反的思想我觉得是很重要的。

Destroying The Graph [POJ - 2125]

细节题意请参见原题。

给定一个 \(n\) 个点，\(m\) 条边的有向图。破坏所有从 \(i\) 点出发的边需要付出 \(a[i]\) 的代价，破坏所有到达 \(i\) 的边需要付出 \(b[i]\) 的代价。问破坏图中所有边的最小代价为多少，并输出破坏方案。

输出最小代价是比较简单的。问题是怎么输出方案，直接看残量网络图中哪些边的剩余流量为 \(0\) 是肯定不行的。

不妨考虑下 \(dfs\)，从源点 \(s\) 开始，对访问到的每一个点打上标记，对于一个入点，如果没访问到它，说明这一条边被割掉了，输出。 对于一个出点，如果访问到它了，说明他之前的所有路径都没有割断，因为跑了最大流后，残量网络中是不存在增广路径的，因此就说明它的这条边被割断了，输出即可。

这种 \(dfs\) 的方式可以用来看做最小割后哪些边被割掉了。

Neerc2006 Hard Life

在一家公司中，人事部经理与业务部经理不和。一次，总经理要求人事部从公司的职员中挑选出一些来帮助业务部经理完成一项任务。人事部经理发现，在公司的所有职员中，有一些人相处得很不好。如果把他们同时放在一个工作小组中，他们将会给主管带来不小的麻烦。人事部经理还知道，在一个工作小组中，主管人员的麻烦程度可以认为是(带来麻烦的人的对数/总人数) 。于是，人事部经理决定选取这样的一些人，使得业务部经理的麻烦度最大。你的任务是帮助人事部经理达到他的目的。当麻烦度最大时，输出选取的总人数。在这样的一个公司中，保证公司的人数小于 \(100\) 人，带来麻烦的员工不会多于 \(1000\) 对。

这是一个 \(01\) 分数规划问题。关于分数规划问题可以参见https://www.cnblogs.com/Judge/p/10173795.html。

这个题，我认为难点仍然是怎么查找人数。

先挂个代码：

void DFS(int u)
{
	vis[u] = 1, ans += (u <= n);
	for(int i = head[u]; i; i = edge[i].next)
		if(edge[i].w >= eps && !vis[edge[i].v]) DFS(edge[i].v);
}