第十五周:比热容比
第十五周实验:比热容比
一、实验目的
- 理解气体比热容比 \(\gamma = \dfrac{C_p}{C_v}\) 的物理意义及其在热学中的重要作用。
- 掌握利用绝热膨胀法(或里德法/克莱门—德索姆法)测量空气比热容比的实验原理。
- 学习压力、温度变化过程中气体热力学过程的分析方法。
- 熟悉气体实验装置的结构及压力测量仪器的使用方法。
- 培养实验数据处理与误差分析能力。
二、实验仪器
根据教材内容,本实验主要仪器包括:
- 比热容比实验装置(容器、阀门系统)
- 压力传感器或 U 形压差计
- 温度计(或环境温度传感器)
- 手动或电动打气装置
- 秒表
- 数据采集与显示系统(若配套)
- 支架及连接管路
三、实验原理
1. 比热容比的定义
气体的比热容比定义为:
\[\gamma = \frac{C_p}{C_v}
\]
其中:
- \(C_p\) 为气体在 等压过程 中的摩尔比热容
- \(C_v\) 为气体在 等容过程 中的摩尔比热容
理想气体中,\(\gamma\) 是表征气体热学性质的重要参数。
2. 绝热膨胀过程的基本关系
理想气体在绝热过程中满足泊松方程:
\[pV^\gamma = \text{常量}
\]
同时也可写为:
\[T^\gamma p^{1-\gamma} = \text{常量}
\]
3. 比热容比的测量思想(克莱门—德索姆法)
实验步骤的物理过程可分为三段:
-
等温充气过程
将容器内气体缓慢充气,使其压力从大气压 \(p_0\) 升高到 \(p_1\),此过程近似为等温过程。 -
绝热膨胀过程
快速打开阀门,气体迅速膨胀至压力 \(p_2 \approx p_0\),该过程近似为绝热过程,温度下降。 -
等容回温过程
关闭阀门后,气体在恒定体积下与外界热交换,温度回升至环境温度,压力上升至 \(p_3\)。
4. 比热容比的计算公式
由热力学关系可推导出比热容比的实验计算公式:
\[\gamma = \frac{\ln \left( \dfrac{p_1}{p_0} \right)}
{\ln \left( \dfrac{p_1}{p_3} \right)}
\]
在使用压差计测量时,设:
- \(h_1 = p_1 - p_0\)
- \(h_2 = p_3 - p_0\)
则公式可写为更便于实验测量的形式:
\[\gamma = \frac{\ln \left( \dfrac{h_1 + p_0}{p_0} \right)}
{\ln \left( \dfrac{h_1 + p_0}{h_2 + p_0} \right)}
\]
在 \(h_1, h_2 \ll p_0\) 的条件下,可近似为:
\[\gamma \approx \frac{h_1}{h_1 - h_2}
\]
四、实验操作步骤
- 检查实验装置气密性,确认阀门连接良好。
- 记录实验室环境温度与大气压 \(p_0\)。
- 缓慢向容器充气,使压力稳定在 \(p_1\),记录对应压差 \(h_1\)。
- 快速打开阀门,使气体发生绝热膨胀,随后立即关闭阀门。
- 等待气体在等容条件下恢复至室温,记录此时压差 \(h_2\)。
- 重复上述测量 5–8 次,取平均值以减小随机误差。
- 根据实验公式计算比热容比 \(\gamma\)。
五、误差分析与不确定度来源
实验误差主要来源包括:
- 绝热过程不完全(阀门开启不够迅速)
- 压力测量仪器分辨率有限
- 气体泄漏导致压力变化
- 环境温度波动
- 人为读数误差
比热容比的不确定度主要由 \(h_1\) 与 \(h_2\) 的测量误差引起,其相对不确定度可通过误差传播公式估算。
六、原始数据
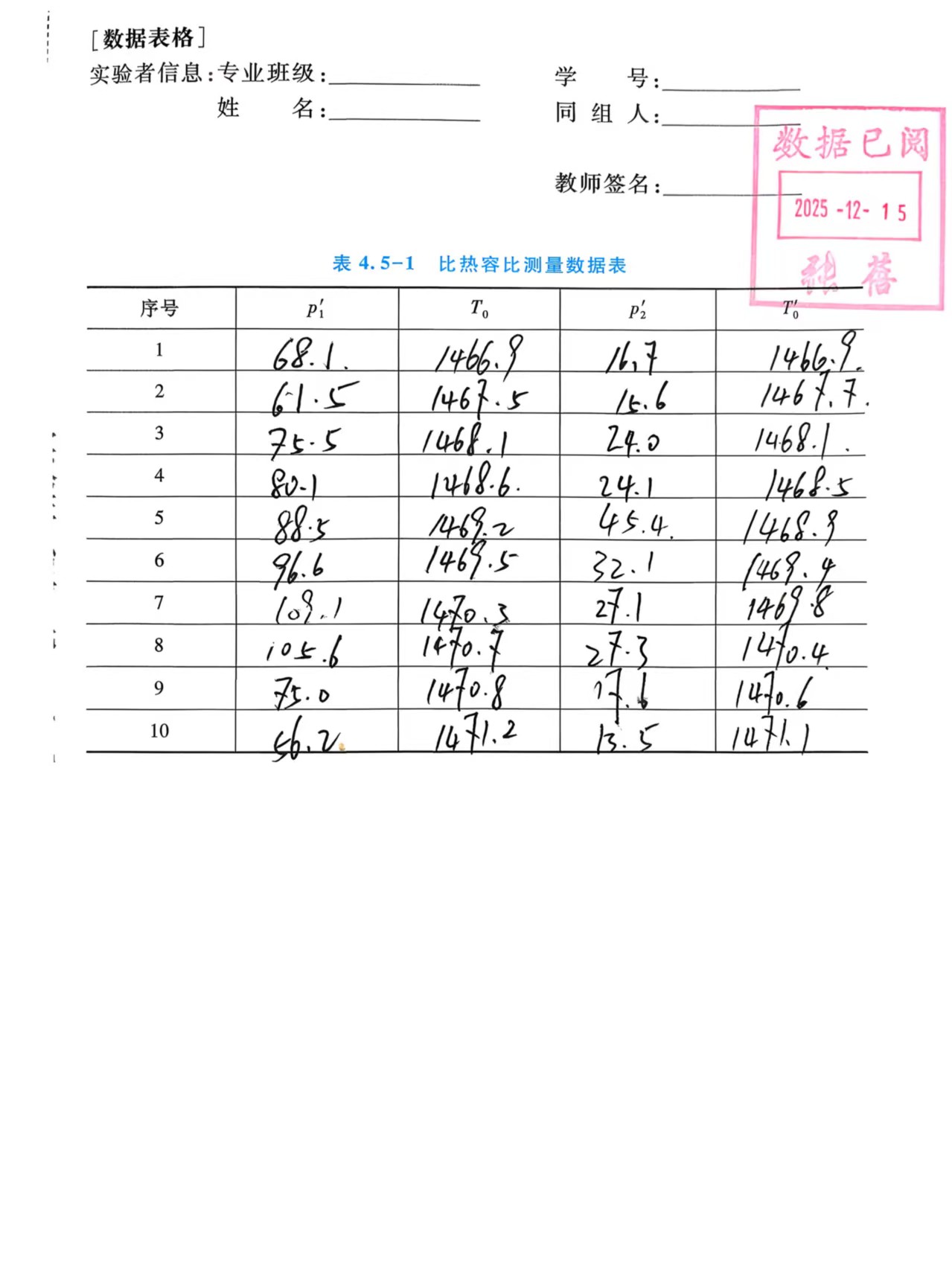
七、数据处理
实验记录空气在绝热膨胀前后的压差读数 \(p_1'\)、\(p_2'\),对应温度 \(T_0\)、\(T_0'\)。
| 序号 | \(p_1'\) | \(T_0\) | \(p_2'\) | \(T_0'\) |
|---|---|---|---|---|
| 1 | 68.1 | 1466.8 | 16.7 | 1466.9 |
| 2 | 61.5 | 1467.5 | 15.6 | 1467.7 |
| 3 | 75.5 | 1468.1 | 24.0 | 1468.1 |
| 4 | 80.1 | 1468.6 | 24.1 | 1468.5 |
| 5 | 88.5 | 1469.2 | 45.4 | 1468.9 |
| 6 | 96.6 | 1469.5 | 32.1 | 1469.4 |
| 7 | 109.1 | 1470.3 | 27.1 | 1469.8 |
| 8 | 105.6 | 1470.7 | 27.3 | 1470.4 |
| 9 | 75.0 | 1470.8 | 17.6 | 1470.6 |
| 10 | 56.2 | 1471.2 | 13.5 | 1471.1 |
---
在 \(p_1', p_2' \ll p_0\) 条件下,比热容比 \(\gamma\) 可近似表示为:
\[\gamma \approx \frac{p_1'}{p_1' - p_2'}
\]
逐条代入公式:
\[\gamma_i = \frac{p_1'}{p_1' - p_2'}
\]
计算结果如下:
| 序号 | \(p_1'\) | \(p_2'\) | \(\gamma\) |
|---|---|---|---|
| 1 | 68.1 | 16.7 | 1.324 |
| 2 | 61.5 | 15.6 | 1.340 |
| 3 | 75.5 | 24.0 | 1.466 |
| 4 | 80.1 | 24.1 | 1.431 |
| 5 | 88.5 | 45.4 | 2.053 |
| 6 | 96.6 | 32.1 | 1.498 |
| 7 | 109.1 | 27.1 | 1.331 |
| 8 | 105.6 | 27.3 | 1.349 |
| 9 | 75.0 | 17.6 | 1.307 |
| 10 | 56.2 | 13.5 | 1.316 |
第 5 组数据计算得到:
\[\gamma_5 = 2.053
\]
该值显著偏离空气理论值 \(\gamma \approx 1.40\),主要原因可能包括:
- 阀门开启时间过长,绝热条件破坏;
- 气体未充分恢复至室温即读数;
- 压差读数误差较大。
因此,按照实验规范,将第 5 组数据作为异常值剔除,不参与平均计算。
对其余 9 组数据取算术平均值:
\[\bar{\gamma} = \frac{1}{9} \sum_{i=1}^{9} \gamma_i
\]
代入数值:
\[\bar{\gamma}
= \frac{
1.324 + 1.340 + 1.466 + 1.431 + 1.498 + 1.331 + 1.349 + 1.307 + 1.316
}{9}
\]
计算得到:
\[\boxed{\bar{\gamma} = 1.374}
\]
- 实验测得空气的比热容比为:
\[\gamma \approx 1.37
\]
- 理论值为空气的比热容比:
\[\gamma_{\text{theory}} \approx 1.40
\]
- 相对偏差约为 \(2\%\),在教学实验允许范围内。
实验结果与理论值基本一致,说明实验方法正确,绝热近似条件总体满足。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号