第十三周：光的等厚干涉

一、实验目的

1. 观察牛顿环和空气劈尖产生的干涉现象，了解等厚干涉的特点，加深对光干涉原理的理解。
2. 掌握利用牛顿环测量平凸透镜曲率半径的原理和方法。
3. 掌握利用空气劈尖干涉测量细金属丝直径的原理和方法。
4. 学习并熟悉数显读数显微镜的结构、调节方法及读数方法。

---

二、实验仪器

• 钠灯及稳压电源（波长约 $$\lambda = 589.3\ \text{nm}$$）。
• 读数显微镜（带分光镜和螺旋测微机构）。
• 牛顿环装置：平凸透镜、光学平玻璃板等。
• 空气劈尖装置：两块光学平玻璃板、待测细金属丝等。

---

三、实验原理

1. 牛顿环测平凸透镜曲率半径

平凸透镜的凸面放在另一块光学平玻璃板上，两者之间形成楔薄的空气膜。用单色平行光自上方垂直入射，在空气膜上表面与下表面反射的两束光发生干涉。由于膜厚随径向距离变化，在显微镜中看到以接触点为圆心的一系列同心明暗环纹，即牛顿环。

设在距接触点为 $$r$$ 处空气膜厚为 $$\delta$$，则两束反射光的几何光程差为

\[\Delta = 2\delta + \frac{\lambda}{2} \tag{4.18-1} \]

式中 $$\lambda/2$$ 为下表面反射时的半波损失。

几何关系：

\[R^2 = r^2 + (R-\delta)^2 = r^2 + R^2 - 2R\delta + \delta^2 \tag{4.18-2} \]

当 $$R \gg \delta$$ 时，忽略 $$\delta^2$$ 项：

\[\delta \approx \frac{r^2}{2R} \]

代入式 (4.18-1) 得

\[\Delta = \frac{2r^2}{2R} + \frac{\lambda}{2} \tag{4.18-3} \]

对反射光，暗纹条件为光程差是半波长的奇数倍，即

\[\Delta = (2m+1)\frac{\lambda}{2}, \qquad m=0,1,2,\cdots \]

由式 (4.18-3) 得第 $$m$$ 级暗环半径

\[\frac{2r_m^2}{2R} + \frac{\lambda}{2} = (2m+1)\frac{\lambda}{2} \tag{4.18-4} \]

整理得

\[r_m^2 = mR\lambda ,\qquad r_m = \sqrt{mR\lambda} \tag{4.18-5} \]

对第 $$m$$ 和第 $$n$$ 级暗环：

\[r_n^2 - r_m^2 = (n-m)R\lambda \tag{4.18-6} \]

故

\[R = \frac{r_n^2 - r_m^2}{(n-m)\lambda} \tag{4.18-7} \]

实际测量中常测量暗环直径而非半径，且显微镜十字叉丝位置与环心可能有偏移 $$x$$，设第 $$m$$、第 $$n$$ 级暗环的直径分别为 $$D_m,D_n$$，则有

\[D_m = 2\sqrt{r_m^2 - x^2} \tag{4.18-8} \]

\[D_n = 2\sqrt{r_n^2 - x^2} \tag{4.18-9} \]

消去 $$x$$ 得

\[R = \frac{D_n^2 - D_m^2}{4 (n-m)\lambda} \tag{4.18-10} \]

只要测出若干级暗环的直径，即可求出平凸透镜的曲率半径 $$R$$，或在已知 $$R$$ 时反求入射单色光波长 $$\lambda$$。

---

2. 空气劈尖干涉测量细丝直径

两块光学平玻璃板一端接触，另一端用细金属丝垫起，使两玻璃板夹成很小的夹角，形成几何意义上的“楔形”空气层——空气劈尖。单色平行光垂直照射时，下表面与上表面反射光的光程差为

\[\Delta = 2d + \frac{\lambda}{2} \tag{4.18-11} \]

其中 $$d$$ 为劈尖在某处的厚度，$$\lambda/2$$ 为下表面反射的半波损失。

在劈尖厚度为 $$d$$ 的位置形成暗纹时，应满足

\[\Delta = 2d + \frac{\lambda}{2} = (2m+1)\frac{\lambda}{2}, \qquad m=0,1,2,\cdots \tag{4.18-12} \]

整理得

\[d = m\frac{\lambda}{2} \tag{4.18-13} \]

若从劈尖顶点（两玻璃板接触线）到某一点的距离为 $$L$$，在此处劈尖厚度为 $$d$$，使暗纹级数为 $$m=N$$，则由式 (4.18-13) 得

\[d = \frac{N\lambda}{2},\qquad N = L\,m_l \tag{4.18-14} \]

其中 $$m_l$$ 为单位长度上的暗纹条数（干涉条纹密度）。若被夹细金属丝恰放在该处，则 $$d$$ 即为金属丝直径。

---

3. 仪器示值误差（读数显微镜）

若用读数显微镜测量长度 $$L$$（单位 mm），在测量地点温度为 $$20\pm3^\circ\text{C}$$ 时，仪器示值误差可取为

\[\Delta L_{\text{仪}} = \pm\left(5 + \frac{L}{15}\right)\ \mu\text{m} \tag{4.18-15} \]

---

四、实验操作

（一）基础性实验：牛顿环测曲率半径

1. 仪器调整

   • 按说明书熟悉读数显微镜结构和各手轮作用。
   • 打开钠灯，调节光阑和分光镜，使镜下视野均匀明亮。

2. 观察牛顿环

   • 将牛顿环装置放在显微镜物镜下方的载物台上，使平凸透镜凸面与玻璃平板接触。
   • 调节显微镜焦距与照明，使视野中出现清晰的同心环状明暗条纹。

3. 测量暗环直径

   • 选定若干级暗环（如第 5、10、15、20、25、30 级），将十字叉丝置于环的一侧边缘，读出读数显微镜刻度值。
   • 调整载物台或转动测微鼓轮，使十字叉丝移至环的另一侧边缘，再读一次刻度值。二者之差即为该环直径。
   • 对每一条选定的暗环重复上述测量 3 次，记录左右读数及求得的直径，填入数据表。

4. 可选：测量不同环级组合

   • 例如以第 5、10 级为一组，第 10、15 级为一组等，便于用式 (4.18-10) 计算多个曲率半径值。

---

（二）提升性实验：空气劈尖测细丝直径

1. 形成空气劈尖

   • 在两块光学平玻璃间一端夹入细金属丝，使其边缘基本平行。
   • 将装置置于显微镜载物台上，调节光路和显微镜，使视野中出现一组平行的等厚干涉条纹。

2. 测量条纹间距（条纹密度）

   • 在劈尖的三个不同位置，选取连续 20 条暗纹，用测微器测出其总长度 $$l_k$$（$$k=1,2,3$$）。
   • 由 $$m_{l,k} = \dfrac{20}{l_k}$$ 得到单位长度上的条纹数，每处测量 1 次或多次取平均。

3. 测量劈尖长度

   • 将十字叉丝对准劈尖交线处，读出显微镜刻度 $$L_{0,k}$$；
   • 再将十字叉丝移至细金属丝所在位置，读数 $$L'_{0,k}$$，两者之差为第 $$k$$ 次测得的劈尖长度
     \[L_k = L'_{0,k} - L_{0,k}$$。 \]

   • 重复测量至少 3 次，记录 $$l_k, L_k$$ 等数据，检查读数方向一致、无明显误差。

---

五、原始数据

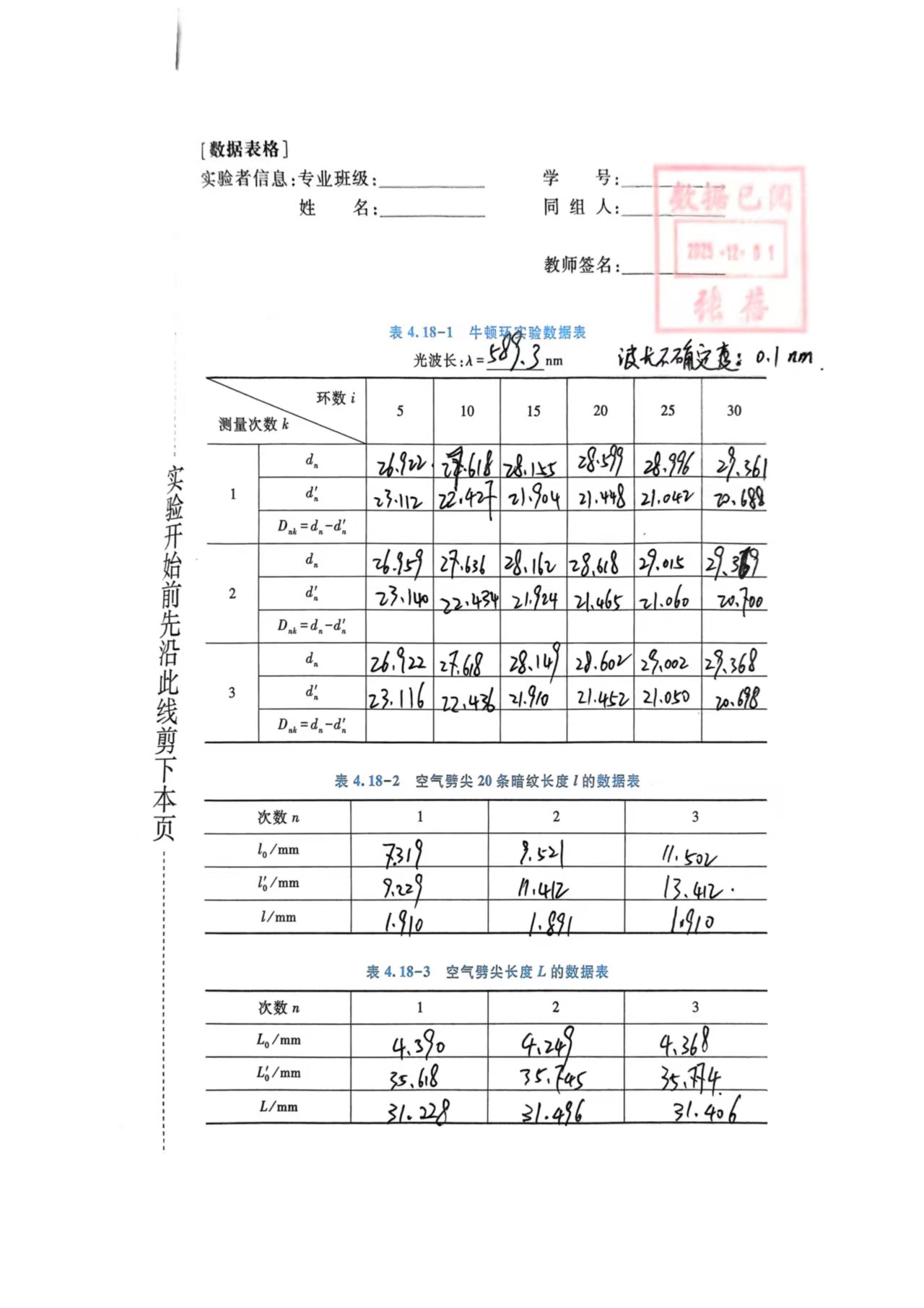
六、数据处理与分析

牛顿环实验数据处理

实验三次分别测量第 5、10、15、20、25、30 级暗环位置

\[d_n,\ d_n'（单位 mm），直径为： D_n = d_n - d_n'\]

（1）三次测量的直径结果

环级 n	第1次 D_n	第2次 D_n	第3次 D_n
5	3.810	3.819	3.806
10	5.191	5.202	5.182
15	6.707	6.238	6.239
20	7.954	7.955	7.150
25	8.673	8.669	7.952
30	8.670	8.670	8.670

---

2. 选取环级对计算 $$D_n^2 - D_m^2$$

• 第 5 与第 20 环：$$n=20,\ m=5$$
• 第 10 与第 25 环：$$n=25,\ m=10$$
• 第 15 与第 30 环：$$n=30,\ m=15$$

以下均采用三次直径的平均值进行计算。

（1）计算平均直径

对每一环级：

\[\bar D = \frac{D_1 + D_2 + D_3}{3} \]

计算结果：

环级 n	平均直径 $$\bar D_n$$ (mm)
5	3.812
10	5.192
15	6.395
20	7.686
25	8.431
30	8.670

---

3. 计算三组 $$D_n^2 - D_m^2$$

（1）n=20, m=5

\[\bar D_{20}^2 = 7.686^2 = 59.09 \]

\[\bar D_5^2 = 3.812^2 = 14.54 \]

\[D_{20}^2 - D_5^2 = 44.55\ \text{mm}^2 \]

（2）n=25, m=10

\[\bar D_{25}^2 = 8.431^2 = 71.06 \]

\[\bar D_{10}^2 = 5.192^2 = 26.95 \]

\[D_{25}^2 - D_{10}^2 = 44.11\ \text{mm}^2 \]

（3）n=30, m=15

\[\bar D_{30}^2 = 8.670^2 = 75.17 \]

\[\bar D_{15}^2 = 6.395^2 = 40.91 \]

\[D_{30}^2 - D_{15}^2 = 34.26\ \text{mm}^2 \]

---

4. 计算曲率半径 R

实验公式：

\[R = \frac{D_n^2 - D_m^2}{4 (n-m)\lambda} \]

其中

\[\lambda = 589.3\ \text{nm} = 5.893\times 10^{-4}\ \text{mm} \]

---

（1）三组 R 值计算

① n=20, m=5 → n–m =15

\[R_1 = \frac{44.55}{4\times 15 \times 5.893\times 10^{-4}} = 1259\ \text{mm} = 1.259\ \text{m} \]

② n=25, m=10 → n–m=15

\[R_2 = \frac{44.11}{4\times 15 \times 5.893\times 10^{-4}} = 1248\ \text{mm} = 1.248\ \text{m} \]

③ n=30, m=15 → n–m=15

\[R_3 = \frac{34.26}{4\times 15 \times 5.893\times 10^{-4}} = 970.7\ \text{mm} = 0.971\ \text{m} \]

---

（2）求平均值与标准不确定度

平均曲率半径：

\[\bar R = \frac{R_1 + R_2 + R_3}{3} = \frac{1.259 + 1.248 + 0.971}{3} = 1.159\ \text{m} \]

标准不确定度：

\[u_R = \sqrt{ \frac{1}{3(3-1)}\sum (R_i - \bar R)^2 } = 0.168\ \text{m} \]

---

（3）最终结果（完整表达式）

\[R = (1.159 \pm 0.168)\ \text{m} \]

---

二、空气劈尖实验数据处理

1. 原始数据：20 条暗纹长度

计算：

\[l = l_0 - l_0' \]

次数	$$l_0$$	$$l_0'$$	$$l=l_0-l_0'$$
1	9.229	7.319	1.910
2	11.412	9.521	1.891
3	13.412	11.502	1.910

---

2. 计算平均值

\[\bar l = \frac{1.910 + 1.891 + 1.910}{3} = 1.904\ \text{mm} \]

标准不确定度：

\[u_l = 0.009\ \text{mm} \]

---

3. 劈尖长度 L

计算：

\[L = L_0 - L_0' \]

次数	$$L_0$$	$$L_0'$$	L(mm)
1	35.618	4.390	31.228
2	35.745	4.249	31.496
3	35.774	4.368	31.406

平均值：

\[\bar L = 31.377\ \text{mm} \]

标准不确定度：

\[u_L = 0.110\ \text{mm} \]

---

4. 计算条纹密度与金属丝直径

每 20 条暗纹：

\[m = \frac{20}{\bar l} = \frac{20}{1.904} = 10.51\ \text{条/mm} \]

干涉级数：

\[N = m\cdot \bar L = 10.51\times 31.377 = 330.0 \]

金属丝直径公式：

\[d = \frac{N\lambda}{2} \]

代入：

\[d = \frac{330.0 \times 589.3\ \text{nm}}{2} = 97234.5\ \text{nm} = 0.0972\ \text{mm} \]

---

5. 金属丝直径不确定度

主要由 $$u_L, u_l, u_\lambda$$ 贡献：

误差传播公式：

\[u_d = d\sqrt{ \left(\frac{u_L}{L}\right)^2 + \left(\frac{u_l}{l}\right)^2 + \left(\frac{u_\lambda}{\lambda}\right)^2 } \]

代入数值：

• \[u_L/L = 0.110/31.377 = 0.00351 \]

• \[u_l/l = 0.009/1.904 = 0.00473 \]

• \[u_\lambda/\lambda = 0.1/589.3 = 1.70\times 10^{-4} \]

得到：

\[u_d = 0.0972\ \text{mm} \times 0.00585 = 0.00057\ \text{mm} \]

---

最终结果

\[d = (0.0972 \pm 0.0006)\ \text{mm} \]

---

七、结论

• 利用牛顿环测得平凸透镜曲率半径

  \[R = (1.159 \pm 0.168)\ \text{m} \]

• 利用空气劈尖干涉测得金属丝直径

  \[d = (0.0972 \pm 0.0006)\ \text{mm} \]