bzoj 2301: [HAOI2011] Problem b

Time Limit: 50 Sec  Memory Limit: 256 MB
Submit: 2833  Solved: 1256
[Submit][Status][Discuss]

Description

对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

Input

第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

Output

共n行，每行一个整数表示满足要求的数对(x,y)的个数

Sample Input

2
2 5 1 5 1
1 5 1 5 2

Sample Output

14
3

HINT

100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

题解：

　　首先先放个PoPoQQQ的ppt，其次再来份题解。(题解中的容斥定理把c和b写反了，无视就好)

　　总结一下，莫比乌斯反演有两种形式

　　形式一：

           　

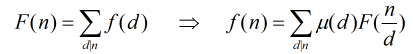
　　形式二：

　　        

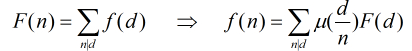
　　本题用到的是第二种形式，题目要求求x∈[a,b]，y∈[c,d]。x和y满足gcd(x,y)==k的x和y的数对数。

　　令f(i)为x∈[1,N]，y∈[1,M]，gcd(x,y)==i 的(x,y)数对数。

　　令F(i)为x∈[1,N]，y∈[1,M]，i|gcd(x,y) 的(x,y)数对数。

　　可以感觉，a和c的限制有些不好处理，不妨先忘掉a,c的限制。再看形式二，考虑f(i)与F(i)的关系，f(i)是gcd(x,y)==i，F(i)是gcd(x,y)==t*i(t∈Z)，所以F(i)=sigma(f(d))(i|d)，所以f(i)与F(i)正好满足形式二的第一个，可以利用莫比乌斯反演用F(i)表示f(i)。而F[i]=[N/i]*[M/i]  ([]表示向下取整)

　　再考虑a和c的限制，设g(x,y,k)表示[1,x],[1,y] gcd(x1,y1)==k的对数，这个式子其实等价于g(x/k,y/k,1)。

　　再有容斥原理可得：Ans=g(b/k,d/k,1)-g((a-1)/k,d/k,1)-g(c/k,b/k,1)+g((a-1)/k,(c-1)/k,1),对于每个g(,,)我们都可以用f()来求。

　　O(n)的复杂度不足以解决此题，还有一个O(sqrt(n))的优化，具体看ppt或题解，讲的很清楚。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
typedef long long LL; 
const LL maxn=50000; 
LL mu[maxn],prime[maxn],sum[maxn],tot,N;
bool not_prime[maxn];
LL a,b,c,d,k,ANS;
inline void pre(){
    memset(not_prime,false,sizeof(not_prime));
    mu[1]=1;
    for(LL i=2;i<=maxn;i++){
        if(not_prime[i]==false){
            prime[++tot]=i;
            mu[i]=-1;
        }
        for(LL j=1;j<=tot;j++){
            if(i*prime[j]>maxn) break;
            not_prime[prime[j]*i]=true;
            if(i%prime[j]==0){
                mu[prime[j]*i]=0;
                break;
            }
            else mu[prime[j]*i]=-mu[i];
        }
    }
}
inline LL solve(LL N,LL M){
    LL ans=0;
    if(N>M) swap(N,M);
    for(LL i=1,la=0;i<=N;i=la+1){
        la=min(N/(N/i),M/(M/i));
        ans+=(sum[la]-sum[i-1])*(N/i)*(M/i);
    }
    return ans;
} 
int main(){
//    freopen("b.in","r",stdin);
//    freopen("b.out","w",stdout);
    pre();
    sum[0]=0;
    for(LL i=1;i<=maxn;i++){
        sum[i]=sum[i-1]+mu[i];
    }
    scanf("%d",&N);
    while(N--){
        scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
        ANS=solve(b/k,d/k)-solve((a-1)/k,d/k)-solve(b/k,(c-1)/k)+solve((a-1)/k,(c-1)/k);
        printf("%lld\n",ANS);
    }
    return 0;
}