斐波那契数列问题的递归和动态规划

斐波那契数列问题的递归和动态规划

题目：斐波那契数 & 爬楼梯 & 斐波那契数列问题的递归和动态规划3

《程序员代码面试指南》第56题 P179 难度：将★★★★

这三个问题本质上都是斐波那契数列的问题。

首先是基本的斐波那契数问题。一共有三种解法。

第一种时间复杂度为O(2^N)，即暴力递归。（也是我解题时想到的方法）

public int f1(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    return f1(n - 1) + f1(n - 2);
}

第二种时间复杂度为O(N)，从左到右依次求出每一项的值。

public int f2(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    int res = 1;
    int pre = 1;
    int tmp = 0;
    for (int i = 3; i <= n; i++) {
        tmp = res;
        res = res + pre;
        pre = tmp;
    }
    return res;
}

第三种时间复杂度为O(logN)，详细解释见斐波那契数-官方题解，用了一种叫矩阵快速幂的方法。

可以得出如下的递推关系

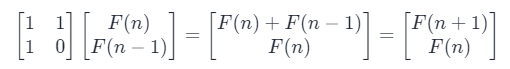
因此

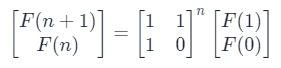
然后该问题就转化为了如何用最快的方法求一个矩阵N次方的问题。

这里举个例子：75的二进制数是1001011，10的75次方=10⁶⁴×10⁸×10²×10¹。

我们可以先求出10¹，再求出10²，然后10⁴……直到10⁶⁴。即75的二进制数形式有多少位，我们就使用了几次乘法。

同时，应当把需要累乘的数相乘。10⁶⁴、10⁸、10²、10¹应该累乘，10³²、10¹⁶、10⁴不应该累乘。应该累乘的幂64、8、2、1对于75二进制数中的1，不应该累乘的幂对应75二进制数中的0。

对矩阵来说同理，求矩阵m的p次方参照如下matrixPower方法，muliMatrix方法是两个矩阵相乘的具体实现。

public int[][] matrixPower(int[][] m, int p) {
    int[][] res = new int[m.length][m[0].length];
    // 先把res设为单位矩阵，相等于整数中的1。
    for (int i = 0; i < res.length; i++) {
        res[i][i] = 1;
    }
    int[][] tmp = m;
    for (; p != 0; p >>= 1) {
        if ((p & 1) != 0) {
            res = muliMatrix(res, tmp);
        }
        tmp = muliMatrix(tmp, tmp);
    }
    return res;
}

public int[][] muliMatrix(int[][] m1, int[][] m2) {
    int[][] res = new int[m1.length][m2[0].length];
    for (int i = 0; i < m1.length; i++) {
        for (int j = 0; j < m2[0].length; j++) {
            for (int k = 0; k < m2.length; k++) {
                res[i][j] += m1[i][k] * m2[k][j];
            }
        }
    }
    return res;
}

方法三的全部过程如下：

public int f3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    int[][] base = { { 1, 1 }, { 1, 0 } };
    int[][] res = matrixPower(base, n - 2);
    return res[0][0] + res[1][0];
}

对于爬楼梯问题，本质还是基本的斐波那契数列，只不过初始项不同：S(1)=1，S(2)=2。

public int s3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return n;
    }
    int[][] base = { { 1, 1 }, { 1, 0 } };
    int[][] res = matrixPower(base, n - 2);
    return 2 * res[0][0] + res[1][0];
}

至于母牛生产问题，首先推导出递推数列C(n)=C(n-1)+C(n-3)，可以理解为C(n) = [C(n-1)-C(n-3)] + 2C(n-3)。

其中2C(n-3)为3年前的全部母牛（第n年时已经成熟）在第n年生产了C(n-3)，加上它们自身，即为2C(n-3)。

而在第n-1年时，比第n-3年多出来的母牛为不成熟母牛，即C(n-1)-C(n-3)，它们在第n年虽然不生产，但是也是总数量的一部分。

最终就得到了递推数列C(n) = [C(n-1)-C(n-3)] + 2C(n-3) = C(n-1) + C(n-3)。

这是一个三阶递推数列，公式如下：

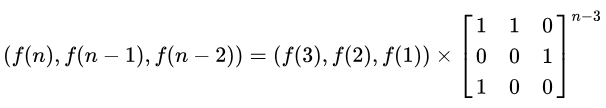
（注意，矩阵在×号左右移动时需要进行转置）

public int c3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2 || n == 3) {
        return n;
    }
    int[][] base = { { 1, 1, 0 }, { 0, 0, 1 }, { 1, 0, 0 } };
    int[][] res = matrixPower(base, n - 3);
    return 3 * res[0][0] + 2 * res[1][0] + res[2][0];
}