ConcurrentHashMap
简介:
ConcurentHashMap是java.util.concurrent包下的一个线程安全的类,继承自Map类,用于存储具有键(key)、值(value)映射关系的双列集合。其数据结构与HashMap类似,都是使用数组+链表+树(红黑树)的结构实现。
CAS:在没有hash冲突时(Node要放在数组上时)
优点
- 线程安全,在高并发情况下与HashTable相比效率更高(HashTable使用粗粒度的synchronize实现)
- 在使用Iterator迭代时不会抛出ConcurrentModificationException异常(fail-fast机制)
数据结构
存储的结构:数组+链表+红黑树
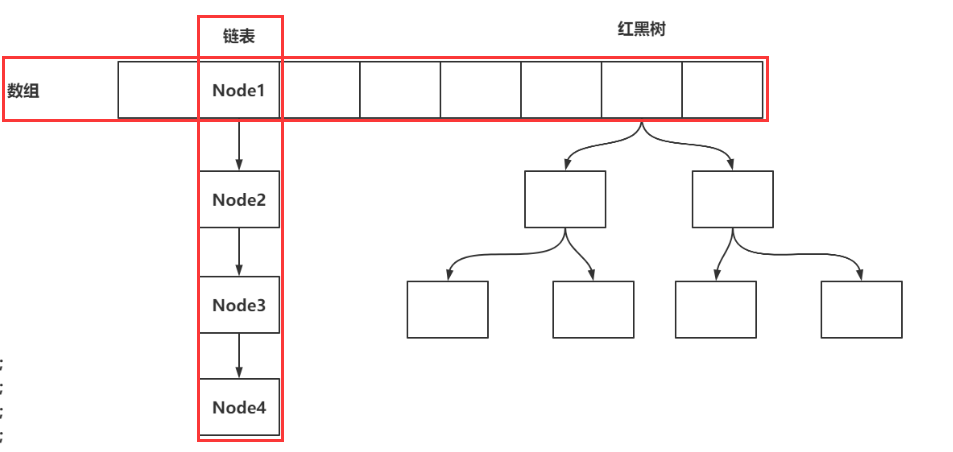
ConcurentHashMap数据结构的实现主要通过Node、TreeNode、TreeBin等内部类实现,其UML图如下:
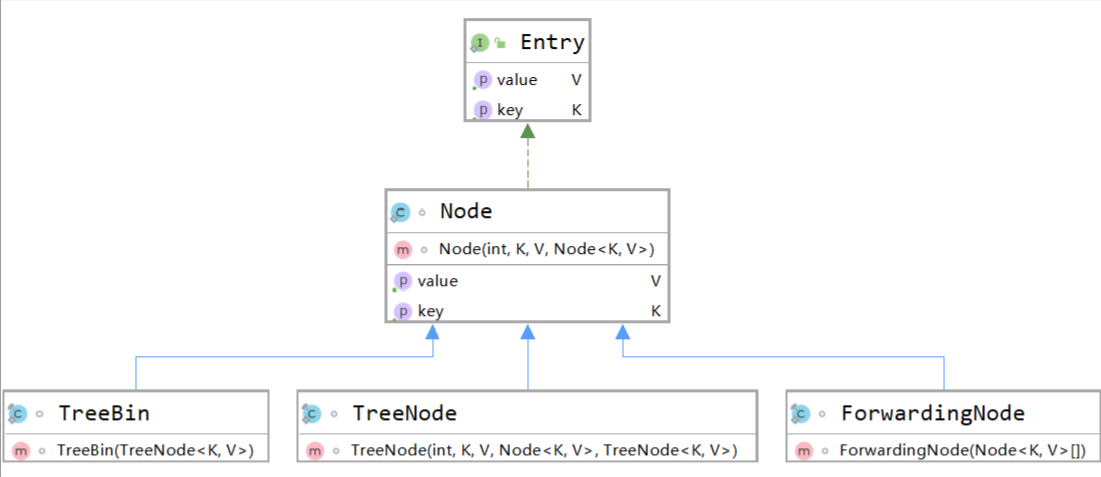
Node
static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; volatile V val; volatile Node<K,V> next; Node(int hash, K key, V val, Node<K,V> next) { //key的hash值 this.hash = hash; this.key = key; this.val = val; // 下一个节点的地址 this.next = next; } }
Node类实现了Entry接口,用于存储节点的hash(哈希值)、key(键)、value(值)以及next(下一个节点的地址)四个属性。
TreeNode
TreeNode继承了Node类,用于存储ConcurentHashMap中的树结构,其属性如下:
static final class TreeNode<K,V> extends Node<K,V> { //父节点 TreeNode<K,V> parent; // 红黑树链接 //左节点 TreeNode<K,V> left; //右节点 TreeNode<K,V> right; //前驱节点 TreeNode<K,V> prev; // 需要在删除时断开连接 //节点有红黑两种颜色 boolean red; }
其构造方法如下:
TreeNode(int hash, K key, V val, Node<K,V> next,
TreeNode<K,V> parent) {
super(hash, key, val, next);
this.parent = parent;
}
在构造方法中,TreeNode调用了Node的构造方法,并指定了该节点的父节点
TreeBin
TreeBin用于包装TreeNode类,当链表过长时,TreeBin会把TreeNode转换为红黑树。事实上,在ConcurentHashMap的“数组”中(也就是树的根节点)所存储的并不是TreeNode而是TreeBin。
TreeBin不存储key/value,TreeBin还维护了一个读写锁,使得读必须等待写操作完成才能进行。
ForwardingNode
ForwardingNode用于标记正在迁移中的Node。在其构造方法会生成一个key、value 和 next 都为 null,且 hash 为 MOVED 的 Node。
static final class ForwardingNode<K,V> extends Node<K,V> {
final Node<K, V>[] nextTable;
ForwardingNode(Node<K, V>[] tab) {
super(MOVED, null, null, null);
this.nextTable = tab;
}
}
是怎么保证线程安全的
1、CAS机制
对数组中节点的修改操作都通过CAS来完成,CAS机制实现了无锁化的修改值的操作,可以大大降低锁代理的性能消耗。
2、volatile关键字
在ConcurentHashMap中,部分变量使用了volatile关键字修饰,保证了变量的可见性和指令的有序性。例如对节点操作进行控制的sizeCtl变量,在Node类中的val、next变量。
3、synchronized
ConcurentHashMap需要使用synchronized对数组中的的非空节点进行加锁操作,这里锁的是该数组位置上的节点(空节点可通过CAS直接进行操作,不需要加锁),如put方法及transfer方法。
4、Unsafe类和三个tabAt方法
Java是无法对操作系统底层进行操作的,所以CAS等操作的具体实现都需要Unsafe类以对底层进行操作。而对于节点的取值、设值、修改等操作,ConcurentHashMap基于Unsafe类封装了三个tabAt方法。
/** * ((long)i << ASHIFT) + ABASE用于计算出元素的真实地址 * ASHIFT为每个节点(Node)的偏移量(位数) * ABASE为头节点的地址(arrayBaseOffset) */ // 获得在i位置上的Node节点 static final <K,V> Node<K,V> tabAt(Node<K,V>[] tab, int i) { return (Node<K,V>)U.getObjectVolatile(tab, ((long)i << ASHIFT) + ABASE); } // 利用CAS算法设置i位置上的Node节点 static final <K,V> boolean casTabAt(Node<K,V>[] tab, int i, Node<K,V> c, Node<K,V> v) { return U.compareAndSwapObject(tab, ((long)i << ASHIFT) + ABASE, c, v); } // 设置节点位置的值 static final <K,V> void setTabAt(Node<K,V>[] tab, int i, Node<K,V> v) { U.putObjectVolatile(tab, ((long)i << ASHIFT) + ABASE, v); }
方法详解
构造函数
ConcurentHashMap有多个重载的构造方法,可传入三个参数
- (int) initialCapacity 指ConcurrentHashMap的初始容量
- (float) loadFactor 加载因子
- (int) concurrencyLevel 并发度
在Java7中,ConcurentHashMap使用Segment分片的形式实现,Segment之间允许线程进行并发操作,而concurrencyLevel则是用来设置Segment[]数组长度的,concurrencyLevel的最小2次幂便为实际并发度。
而在Java8中,ConcurentHashMap摒弃了Segment,改用CAS加上TreeBin等辅助类实现,并发度concurrencyLevel也就没有实际意义了。
public ConcurrentHashMap(int initialCapacity) { if (initialCapacity < 0) throw new IllegalArgumentException(); // MAXIMUM_CAPACITY = 1 << 30(2^30 = 1073741824) // 如果大小为MAXIMUM_CAPACITY最大总量的一半,那么直接将容量设为MAXIMUM_CAPACITY,否则计算最小幂次方 int cap = ((initialCapacity >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : // 1.5 * initialCapacity + 1 tableSizeFor(initialCapacity + (initialCapacity >>> 1) + 1)); this.sizeCtl = cap; }
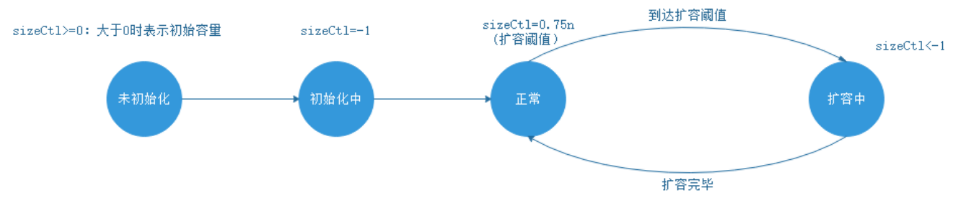
构造函数进行了sizeCtl的赋值,sizeCtl是数组在初始化和扩容操作时的一个控制变量,不同的数值代表不同的意义
- -1代表正在初始化
- 小于-1:低16位代表当前数组正在扩容的线程个数(如果1个线程扩容,值为-2,如果2个线程扩容,值为-3)
- 0:代表数组还没初始化
- 大于0:代表当前数组的扩容阈值,或者是当前数组的初始化大小
- 初始化之后,它的值始终是当前ConcurrentHashMap容量的0.75倍
final V putVal(K key, V value, boolean onlyIfAbsent) { // 省略部分代码………… // 将Map的数组赋值给tab,死循环 for (Node<K,V>[] tab = table;;) { // 声明了一堆变量~~ // n:数组长度 // i:当前Node需要存放的索引位置 // f: 当前数组i索引位置的Node对象 // fn:当前数组i索引位置上数据的hash值 Node<K,V> f; int n, i, fh; // 判断当前数组是否还没有初始化 if (tab == null || (n = tab.length) == 0) // 将数组进行初始化。 tab = initTable(); // 基于 (n - 1) & hash 计算出当前Node需要存放在哪个索引位置 // 基于tabAt获取到i位置的数据 else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { // 现在数组的i位置上没有数据,基于CAS的方式将数据存在i位置上 if (casTabAt(tab, i, null,new Node<K,V>(hash, key, value, null))) // 如果成功,执行break跳出循环,插入数据成功 break; } // 判断当前位置数据是否正在扩容…… else if ((fh = f.hash) == MOVED) // 让当前插入数据的线程协助扩容 tab = helpTransfer(tab, f); // 省略部分代码………… } // 省略部分代码………… }
initTable(初始化数组方法)
private final Node<K,V>[] initTable() { // 声明标识 Node<K,V>[] tab; int sc; // 再次判断数组没有初始化,并且完成tab的赋值 while ((tab = table) == null || tab.length == 0) { // 将sizeCtl赋值给sc变量,并判断是否小于0 if ((sc = sizeCtl) < 0) Thread.yield(); // 可以尝试初始化数组,线程会以CAS的方式,将sizeCtl修改为-1,代表当前线程可以初始化数组 else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { // 尝试初始化! try { // 再次判断当前数组是否已经初始化完毕。 if ((tab = table) == null || tab.length == 0) { // 开始初始化, // 如果sizeCtl > 0,就初始化sizeCtl长度的数组 // 如果sizeCtl == 0,就初始化默认的长度 int n = (sc > 0) ? sc : DEFAULT_CAPACITY; // 初始化数组! Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; // 将初始化的数组nt,赋值给tab和table table = tab = nt; // sc赋值为了数组长度 - 数组长度 右移 2位 16 - 4 = 12 // 将sc赋值为下次扩容的阈值 sc = n - (n >>> 2); } } finally { // 将赋值好的sc,设置给sizeCtl sizeCtl = sc; } break; } } return tab; }
互斥同步进入阻塞状态需要很大的开销,initTable方法使用了自旋锁,通过Thread.yield()使线程让步,然后忙循环直到sizeCtl满足条件
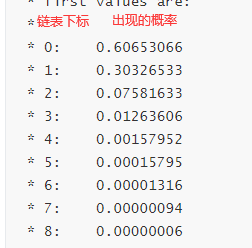
为什么链表长度为8转换为红黑树,不是能其他数值嘛?
答案:泊松分布,可以看出,长度达到8时概率已经很小了
tableSizeFor函数详解(返回大于输入参数且最近的2的整数次幂的数)
/** * 使最高位的1后面的位全变为1,最后再让结果n+1,即得到了2的整数次幂的值 */ private static final int tableSizeFor(int c) { int n = c - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }
put(实际调用putVal方法)
final V putVal(K key, V value, boolean onlyIfAbsent) { // 判空,key和value不能为空 if (key == null || value == null) throw new NullPointerException(); // spread将较高的哈希值扩展为较低的哈希值,并将最高位强制为0 int hash = spread(key.hashCode()); // binCount用于记录相应链表的长度 int binCount = 0; // 死循环 for (Node<K,V>[] tab = table;;) { Node<K,V> f; int n, i, fh; // tab为空,初始化table if (tab == null || (n = tab.length) == 0) tab = initTable(); // 根据hash值计算出在table里面的位置,若该位置的值为空,直接放入元素 else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value, null))) break; // no lock when adding to empty bin } // 存在节点,说明发生了hash碰撞,需要对表进行扩容 // 如果该位置的节点存在值且为MOVED(-1),说明正在扩容 else if ((fh = f.hash) == MOVED) // helpTransfer方法用于增加线程以协助扩容 tab = helpTransfer(tab, f); else { V oldVal = null; // 节点上锁 synchronized (f) { if (tabAt(tab, i) == f) { // fh > 0 说明这个节点是一个链表的节点 不是树的节点 if (fh >= 0) { binCount = 1; // 遍历节点 for (Node<K,V> e = f;; ++binCount) { K ek; // 存在该key,替换其值 if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; if (!onlyIfAbsent) e.val = value; break; } Node<K,V> pred = e; // 不存在该key,插入新Node if ((e = e.next) == null) { pred.next = new Node<K,V>(hash, key, value, null); break; } } } // 树节点 else if (f instanceof TreeBin) { Node<K,V> p; binCount = 2; if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key, value)) != null) { oldVal = p.val; if (!onlyIfAbsent) p.val = value; } } } } if (binCount != 0) { // TREEIFY_THRESHOLD = 8 // 链表长度达到临界值8,转换为树节点 if (binCount >= TREEIFY_THRESHOLD) treeifyBin(tab, i); if (oldVal != null) return oldVal; break; } } } // 将当前ConcurrentHashMap的元素数量+1 addCount(1L, binCount); return null; }
putVal()方法大概的流程图如下:
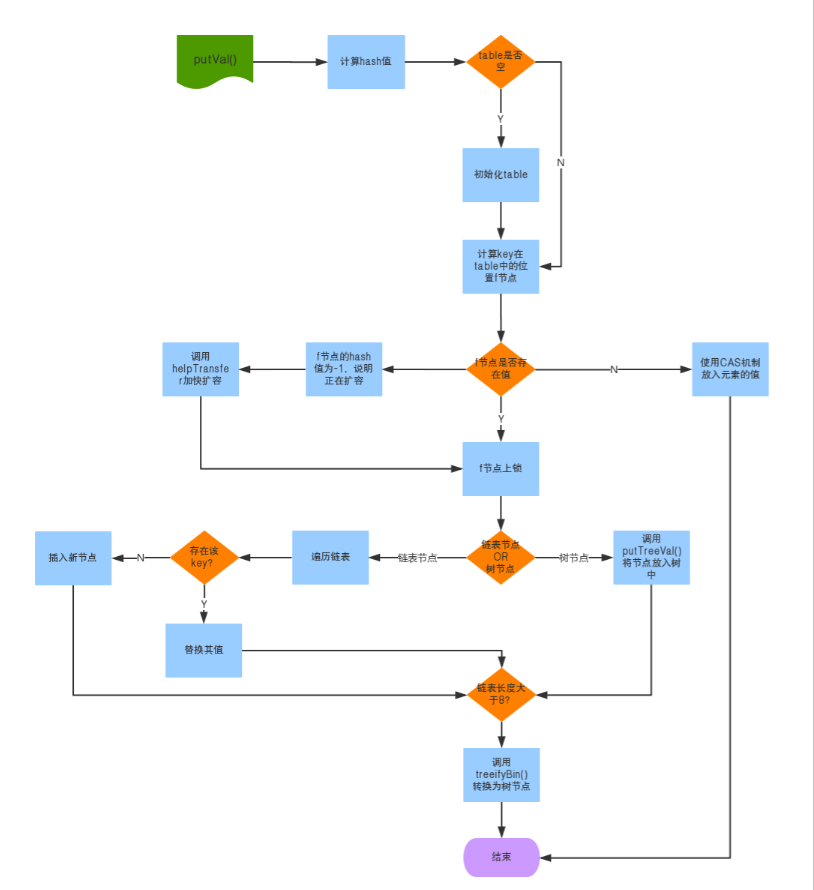
treeifyBin(尝试扩容或者转为红黑树,)
private final void treeifyBin(Node<K,V>[] tab, int index) { Node<K,V> b; int n, sc; if (tab != null) { // 数组的长度小于64(MIN_TREEIFY_CAPACITY=64)时,进行扩容 if ((n = tab.length) < MIN_TREEIFY_CAPACITY) // 调用tryPresize进行扩容(所传参数n即数组长度 * 2,即每次扩容都是增大2倍) tryPresize(n << 1); // 开启链表转红黑树操作 // 当前桶内有数据,并且是链表结构 else if ((b = tabAt(tab, index)) != null && b.hash >= 0) { synchronized (b) { // 再次判断数据是否有变化,DCL if (tabAt(tab, index) == b) { // 开启准备操作,将之前的链表中的每一个Node,封装为TreeNode,作为双向链表 // hd:是整个双向链表的第一个节点。 // tl:是单向链表转换双向链表的临时存储变量 TreeNode<K,V> hd = null, tl = null; // 遍历链表,建立红黑树 for (Node<K,V> e = b; e != null; e = e.next) { TreeNode<K,V> p = new TreeNode<K,V>(e.hash, e.key, e.val, null, null); if ((p.prev = tl) == null) hd = p; else tl.next = p; tl = p; } // hd就是整个双向链表 // TreeBin的有参构建,将双向链表转为了红黑树 setTabAt(tab, index, new TreeBin<K,V>(hd)); } } } } }
tryPresize(扩容)
// size是将之前的数组长度 左移 1位得到的结果 private final void tryPresize(int size) { // 如果扩容的长度达到了最大值,就使用最大值 // 否则需要保证数组的长度为2的n次幂 // 这块的操作,是为了初始化操作准备的,因为调用putAll方法时,也会触发tryPresize方法 // 如果刚刚new的ConcurrentHashMap直接调用了putAll方法的话,会通过tryPresize方法进行初始化 int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : tableSizeFor(size + (size >>> 1) + 1); // 这些代码和initTable一模一样 // 声明sc int sc; // 将sizeCtl的值赋值给sc,并判断是否大于0,这里代表没有初始化操作,也没有扩容操作 while ((sc = sizeCtl) >= 0) { // 将ConcurrentHashMap的table赋值给tab,并声明数组长度n Node<K,V>[] tab = table; int n; // 数组是否需要初始化 if (tab == null || (n = tab.length) == 0) { // 进来执行初始化 // sc是初始化长度,初始化长度如果比计算出来的c要大的话,直接使用sc,如果没有sc大, // 说明sc无法容纳下putAll中传入的map,使用更大的数组长度 n = (sc > c) ? sc : c; // 设置sizeCtl为-1,代表初始化操作 if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { try { // 再次判断数组的引用有没有变化 if (table == tab) { // 初始化数组 Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; // 数组赋值 table = nt; // 计算扩容阈值 sc = n - (n >>> 2); } } finally { // 最终赋值给sizeCtl sizeCtl = sc; } } } // 如果计算出来的长度c如果小于等于sc,直接退出循环结束方法 // 数组长度大于等于最大长度了,直接退出循环结束方法 else if (c <= sc || n >= MAXIMUM_CAPACITY) break; // 省略部分代码 } }
transfer
红黑树操作
-
每个节点必须是红色或者黑色。
-
根节点必须是黑色。
-
如果当前节点是红色,子节点必须是黑色
-
所有叶子节点都是黑色。
-
从任意节点到每个叶子节点的路径中,黑色节点的数量是相同的。
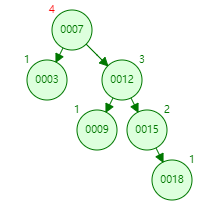
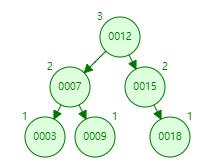
右旋:
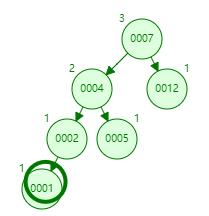
TreeBin()
// 将双向链表转为红黑树的操作。 b:双向链表的第一个节点 // TreeBin继承自Node,root:代表树的根节点,first:双向链表的头节点 TreeBin(TreeNode<K,V> b) { // 构建Node,并且将hash值设置为-2 super(TREEBIN, null, null, null); // 将双向链表的头节点赋值给first this.first = b; // 声明r的TreeNode,最后会被赋值为根节点 TreeNode<K,V> r = null; // 遍历之前封装好的双向链表 for (TreeNode<K,V> x = b, next; x != null; x = next) { next = (TreeNode<K,V>)x.next; // 先将左右子节点清空 x.left = x.right = null; // 如果根节点为null,第一次循环 if (r == null) { // 将第一个节点设置为当前红黑树的根节点 x.parent = null; // 根节点没父节点 x.red = false; // 不是红色,是黑色 r = x; // 将当前节点设置为r } // 已经有根节点,当前插入的节点要作为父节点的左子树或者右子树 else { // 拿到了当前节点key和hash值。 K k = x.key; int h = x.hash; Class<?> kc = null; // 循环? for (TreeNode<K,V> p = r;;) { // dir:如果为-1,代表要插入到父节点的左边,如果为1,代表要插入的父节点的右边 // ph:是父节点的hash值 int dir, ph; // pk:是父节点的key K pk = p.key; // 父节点的hash值,大于当前节点的hash值,就设置为-1,代表要插入到父节点的左边 if ((ph = p.hash) > h) dir = -1; // 父节点的hash值,小于当前节点的hash值,就设置为1,代表要插入到父节点的右边 else if (ph < h) dir = 1; // 父节点的hash值和当前节点hash值一致,基于compare方式判断到底放在左子树还是右子树 else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) dir = tieBreakOrder(k, pk); // 拿到当前父节点。 TreeNode<K,V> xp = p; // 将p指向p的left、right,并且判断是否为null // 如果为null,代表可以插入到这位置。 if ((p = (dir <= 0) ? p.left : p.right) == null) { // 进来就说明找到要存放当前节点的位置了 // 将当前节点的parent指向父节点 x.parent = xp; // 根据dir的值,将父节点的left、right指向当前节点 if (dir <= 0) xp.left = x; else xp.right = x; // 插入一个节点后,做一波平衡操作 r = balanceInsertion(r, x); break; } } } } // 将根节点复制给root this.root = r; // 检查红黑树结构 assert checkInvariants(root); }
// 红黑树的插入动画:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html // 红黑树做自平衡以及保证特性的操作。 root:根节点, x:当前节点 static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) { // 先将节点置位红色 x.red = true; // xp:父节点 // xpp:爷爷节点 // xppl:爷爷节点的左子树 // xxpr:爷爷节点的右子树 for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { // 拿到父节点,并且父节点为红 if ((xp = x.parent) == null) { // 当前节点为根节点,置位黑色 x.red = false; return x; } // 父节点不是红色,爷爷节点为null else if (!xp.red || (xpp = xp.parent) == null) // 什么都不做,直接返回 return root; // ===================================== // 左子树的操作 if (xp == (xppl = xpp.left)) { // 通过变色满足红黑树特性 if ((xppr = xpp.right) != null && xppr.red) { // 叔叔节点和父节点变为黑色 xppr.red = false; xp.red = false; // 爷爷节点置位红色 xpp.red = true; // 让爷爷节点作为当前节点,再走一次循环 x = xpp; } else { // 如果当前节点是右子树,通过父节点的左旋,变为左子树的结构 if (x == xp.right) {、 // 父节点做左旋操作 root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { // 父节点变为黑色 xp.red = false; if (xpp != null) { // 爷爷节点变为红色 xpp.red = true; // 爷爷节点做右旋操作 root = rotateRight(root, xpp); } } } } // 右子树(只需知道左子树就足够了,因为业务都是一样的) else { if (xppl != null && xppl.red) { xppl.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.left) { root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateLeft(root, xpp); } } } } } }
确定左子树和右子数之后,直接维护双向链表和红黑树结构,并且再判断是否需要自平衡。
// 添加节点到红黑树内部 final TreeNode<K,V> putTreeVal(int h, K k, V v) { // Class对象 Class<?> kc = null; // 搜索节点 boolean searched = false; // 死循环,p节点是根节点的临时引用 for (TreeNode<K,V> p = root;;) { // dir:确定节点是插入到左子树还是右子数 // ph:父节点的hash值 // pk:父节点的key int dir, ph; K pk; // 根节点是否为诶null,把当前节点置位根节点 if (p == null) { first = root = new TreeNode<K,V>(h, k, v, null, null); break; } // 判断当前节点要放在左子树还是右子数 else if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; // 如果key一致,直接返回p,由putVal去修改数据 else if ((pk = p.key) == k || (pk != null && k.equals(pk))) return p; // hash值一致,但是key的==和equals都不一样,基于Compare去判断 else if ((kc == null && (kc = comparableClassFor(k)) == null) || // 基于compare判断也是一致,就进到if判断 (dir = compareComparables(kc, k, pk)) == 0) { // 开启搜索,查看是否有相同的key,只有第一次循环会执行。 if (!searched) { TreeNode<K,V> q, ch; searched = true; if (((ch = p.left) != null && (q = ch.findTreeNode(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.findTreeNode(h, k, kc)) != null)) // 如果找到直接返回 return q; } // 再次判断hash大小,如果小于等于,返回-1 dir = tieBreakOrder(k, pk); } // xp是父节点的临时引用 TreeNode<K,V> xp = p; // 基于dir判断是插入左子树还有右子数,并且给p重新赋值 if ((p = (dir <= 0) ? p.left : p.right) == null) { // first引用拿到 TreeNode<K,V> x, f = first; // 将当前节点构建出来 first = x = new TreeNode<K,V>(h, k, v, f, xp); // 因为当前的TreeBin除了红黑树还维护这一个双向链表,维护双向链表的操作 if (f != null) f.prev = x; // 维护红黑树操作 if (dir <= 0) xp.left = x; else xp.right = x; // 如果如节点是黑色的,当前节点红色即可,说明现在插入的节点没有影响红黑树的平衡 if (!xp.red) x.red = true; else { // 说明插入的节点是黑色的 // 加锁操作 lockRoot(); try { // 自平衡操作。 root = balanceInsertion(root, x); } finally { // 释放锁操作 unlockRoot(); } } break; } } // 检查一波红黑树结构 assert checkInvariants(root); // 代表插入了新节点 return null; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号