- 2025.8.31
- 2025.9.1
- 2025.9.2
- 2025.9.3
- 2025.9.9
- 2025.9.14
- 2025.9.18
- 3.4 傅里叶变换的性质 III
- 3.4* 信号的能量谱与功率谱
- 2025.9.29
3.1连续时间周期信号的傅里叶级数
狄利克雷条件:
\[\begin{align}
&在一个周期内 :
\begin{cases}
函数连续或只有有限个第一类间断点\\ \\
有有限个极大、极小值\\ \\
函数绝对可积
\end{cases}
\end{align}
\]
三角形式的傅里叶级数
三角形式傅里叶级数的定义
给定周期为\(T\)的周期信号\(f(t)\),当满足狄利克雷条件时,可以表示为\((t_{0},t_{0}+T)\)上的完备正交函数集合\(\{ 1,\cos n\Omega t,\sin n\Omega t \}\ \left( n\to \infty,\Omega=\frac{2\pi}{T} \right)\)中各个函数的线性组合 :
\[f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}(a_{n}\cos n\Omega t+b_{n}\sin n\Omega t)
\]
其中:
- 直流分量:\(\frac{a_{0}}{2}\)
- \(n\)次余弦分量:\(a_{n}\cos n\Omega t\),\(n\)次正弦分量:\(b_{n}\sin n\Omega t\)
- 基波角频率:\(\Omega=\frac{2\pi}{T}\)
- 基波频率:\(f=\frac{1}{T}\)
\[\begin{align}
&\frac{a_{0}}{2}=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)dt\\ \\
&a_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\cos n\Omega tdt\\ \\
&b_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\sin n\Omega tdt
\end{align}
\]
三角级数的直流、基波、谐波分量
同频率项合并:(辅助角)
\[\begin{align}
&f(t)=\frac{A_{0}}{2}+\sum_{n=1}^{\infty}A_{n}\cos(n\Omega t+\varphi_{n})\\ \\
&其中:\\ \\
&A_{0}=a_{0},A_{n}=\sqrt{ a_{n}^{2}+b_{n}^{2} },\varphi_{n}=-\arctan \frac{b_{n}}{a_{n}}\\ \\
&a_{n}=A_{n}\cos \varphi_{n},b_{n}=-A_{n}\sin \varphi_{n}
\end{align}
\]
上式表明:任何满足狄利克雷条件的周期信号都可以分解为直流分量,基波分量和无穷多项谐波分量之和。其中各次谐波分量的角频率必然是基波频率的整数倍
\[\begin{align}
&直流分量:\frac{A_{0}}{2}=\frac{a_{0}}{2}=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)dt\\ \\
&基波分量(n=1):A_{1}\cos(\Omega t+\varphi_{1})\\ \\
&n次谐波分量(n\neq 1):A_{n}\cos(n\Omega t+\varphi_{n})
\end{align}
\]
\[f(t)=直流+基波+谐波
\]
傅里叶系数的奇偶性
将系数视为谐波次数\(n\)或者\(n\)倍基波角频率\(n\Omega\)的函数,以\(n\)或者\(n\Omega\)为自变量进行分析:
\[\begin{align}
&a_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\cos n\Omega tdt\quad a_{-n}=a_{n}\quad 为n的偶函数\\ \\
&b_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\sin n\Omega tdt\quad b_{-n}=-b_{n}\quad 为n的奇函数\\ \\
&A_{n}=\sqrt{ a_{n}^{2}+b_{n}^{2} }\quad A_{-n}=A_{n}\quad 为n的偶函数\\ \\
&\varphi_{n}=-\arctan \frac{b_{n}}{a_{n}}\quad \varphi_{-n}=-\varphi_{n}\quad 为n的奇函数
\end{align}
\]
信号的对称性与傅里叶系数的关系
信号为\(t\)的偶函数
- \(f(t)\cos n\Omega t\)为偶函数,\(f(t)\sin n\Omega t\)为奇函数
- \(a_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\cos n\Omega tdt=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(t)\cos n\Omega tdt\)
- \(b_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\sin n\Omega tdt=0\)
- 此时,傅里叶级数不包含正弦项:\(f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\cos n\Omega t\)
信号为\(t\)的奇函数
- \(f(t)\cos n\Omega t\)为奇函数,\(f(t)\sin n\Omega t\)为偶函数
- \(a_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\cos n\Omega tdt=0\)
- \(b_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\sin n\Omega tdt=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(t)\sin n\Omega tdt\)
- 此时,傅里叶级数不包含直流和余弦项:\(f(t)=\sum_{n=1}^{\infty}b_{n}\sin n\Omega t\)
信号为半波对称函数

\(f(t)=f\left( t\pm \frac{T}{2} \right)\)信号沿时间轴平移半个周期以后与原波形完全重合
\[\Omega=\frac{2\pi}{T}\implies \Omega'=\frac{2\pi}{\frac{T}{2}}=\frac{4\pi}{T}=2\Omega
\]
- 信号实际周期为\(\frac{T}{2}\),\(2\Omega\)为实际的基波角频率,故只含有\(\Omega\)的偶次谐波
- 此时傅里叶级数只含有偶次谐波,不含奇次谐波,又称为偶谐函数
- 此处的偶谐函数是相对于原函数而言的,因为实际上可以直接令\(T'=\frac{T}{2}\)
信号为半波镜像对称函数

\(f(t)=-f\left( t\pm \frac{T}{2} \right)\)信号平移半个周期以后与原波形关于横轴对称
\[\begin{align}
&a_{0}=a_{2}=\dots=a_{2n}=b_{0}=b_{2}=\dots=b_{2n}=0\\ \\
&a_{1},a_{3},\dots,a_{2n+1},b_{1},b_{3},\dots,b_{2n+1}\neq 0
\end{align}
\]
- 此时傅里叶级数只含有奇次谐波,不含偶次谐波,又称为奇谐函数
任意信号分解为偶分量和奇分量之和
\[f(t)= \frac{f(t)+f(-t)}{2}+ \frac{f(t)-f(-t)}{2}=f_{ev}(t)+f_{od}(t)
\]
其中:
- \(ev\to even,od\to odd\)
- 偶分量:\(f_{ev}(t)=\frac{f(t)+f(-t)}{2}\)
- 奇分量:\(f_{od}(t)= \frac{f(t)-f(-t)}{2}\)
指数形式的傅里叶级数
指数形式的傅里叶级数的定义
给定周期为\(T\)的周期信号\(f(t)\),当它满足狄利克雷条件时,可以表示为\((t_{0},t_{0}+T)\)上完备正交函数集合\(\{ e^{jn\Omega t} \}\left( n\to \infty,\Omega=\frac{2\pi}{T} \right)\)中各个函数的线性组合:
\[\begin{align}
&f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}\\ \\
&F_{n}=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)e^{-jn\Omega t}dt
\end{align}
\]
指数形式傅里叶级数中出现了负频率,负频率没有实际的物理意义,它的出现完全是采用复指数信号集合表示周期信号的结果,是数学分析的过程,当正负频率合并在一起的时候才能合成实际的频率分量
指数形式与三角形式傅里叶系数的关系
\[\begin{align}
F_{n}&=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)e^{-jn\Omega t}dt=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)\cos n\Omega tdt-j \frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)\sin n\Omega tdt\\ \\
&=\frac{1}{2}(a_{n}-jb_{n})\\ \\
F_{-n}&=\frac{1}{2}(a_{-n}-jb_{-n})=\frac{1}{2}(a_{n}+jb_{n})\\ \\
\implies&\begin{cases}
a_{n}=F_{n}+F_{-n}\\ \\
b_{n}=j(F_{n}-F_{-n})
\end{cases}
\end{align}
\]
对于复数\(F_{n}\),可以转换为\(F_{n}=|F_{n}|\cdot e^{j\cdot\angle F_{n}}\)
\[\begin{align}
&|F_{n}|=\frac{1}{2}\sqrt{ a_{n}^{2}+b_{n}^{2} }=\frac{1}{2}A_{n}\ ,\ |F_{n}|=|F_{-n}|\quad 为n的偶函数\\ \\
&\angle F_{n}=-\arctan \frac{b_{n}}{a_{n}}=\varphi_{n}\ ,\ \varphi_{-n}=-\varphi_{n}\quad 为n的奇函数\\ \\
&\therefore F_{n}=\frac{1}{2}A_{n}e^{j\varphi_{n}}
\end{align}
\]
例
求图示周期信号的指数形式傅里叶级数
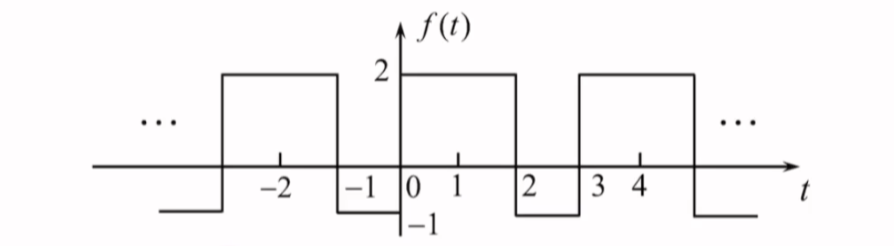
\[\begin{align}
&T=3,\Omega=\frac{2\pi}{T}=\frac{2\pi}{3}\\ \\
F_{n}&=\frac{1}{T}\int_0^{T}f(t)e^{-jn\Omega t} dt=\frac{1}{3}\left[ 2\int_{0}^{2}e^{-jn\Omega t}dt-\int_{2}^{3}e^{-jn\Omega t}dt \right]\\ \\
&=\frac{2}{3}\cdot \frac{1}{j\cdot3n\Omega}e^{-jn\Omega t}\bigg|_{0}^{2}-\frac{1}{3}\cdot \frac{1}{-j\cdot n\Omega}e^{-jn\Omega t}\bigg|_{2}^{3}\\ \\
&=\frac{2-3e^{-j\cdot 2n\Omega}+e^{-j\cdot 3n\Omega}}{j\cdot 3n\Omega}\\ \\
&将\Omega=\frac{2\pi}{3}代入得:\\ \\
原式&=\frac{2-3e^{-j\cdot \frac{4\pi}{3}n}+e^{-j\cdot 2\pi n}}{j\cdot 2\pi n}\\ \\
&由于e^{-j\cdot 2\pi n}=\cos_{}2\pi n-j\cdot \sin 2\pi n=1:\\ \\
原式&=\frac{3}{j\cdot 2\pi n}\left( 1-e^{j\cdot \frac{4\pi}{3}n} \right)\\ \\
&\therefore f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}=\sum_{n=-\infty}^{\infty}\frac{3}{j\cdot 2\pi n}\left( 1-e^{j\cdot \frac{4\pi}{3}n} \right)e^{jn \frac{2\pi}{3}t}
\end{align}
\]
- 在最后一步化简的时候,可以将复数展开为三角形式,判断是否可以进一步整理成常数
3.2 连续时间周期信号的频谱分析
周期信号的频谱
频谱的概念
为了直观表示信号各个频率分量的分布及其所占比重,引入频谱的概念
\[\begin{align}
&幅频特性:A_{n},F_{n}\sim n\Omega\\ \\
&相频特性:\varphi_{n}\sim n\Omega
\end{align}
\]
\[频谱\begin{cases}
幅度谱(幅频特性曲线):幅度A_{n}(|F_{n}|)随离散频率n\Omega变化的图\\ \\
相位谱(相频特性曲线):相位\varphi_{n}随离散频率n\Omega变化的图
\end{cases}
\]
- 频谱为离散谱,\(\omega=n\Omega\)必然是基波\(\Omega\)的整数倍
单边频谱与双边频谱
单边频谱
\[f(t)=\frac{A_{0}}{2}+\sum_{n=1}^{\infty}A_{n}\cos(n\Omega t+\varphi_{n})
\]
信号分解为三角级数时可以用单边频谱表示,此时频谱中只有正频率分量
双边频谱
\[f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}
\]
信号分解为指数型级数时可以用双边频谱表示,此时频谱中同时有正、负频率分量
单边频谱与双边频谱的关系
\[F_{n}=\frac{1}{2}A_{n}e^{j\varphi_{n}}
\]
- 单边幅度谱除了直流分量之外幅度减半且关于纵轴偶对称即可得到双边幅度谱
- 单边相位谱关于纵轴奇对称即可得到双边相位谱
- \(|F_{n}|= \frac{1}{2}A_{n}\)
作频谱图的说明
- 作单边频谱图:
- 需要注意周期信号各个分量必须是余弦\(\cos\)函数相加的形式,若所给的信号里有\(sin\)形式的分量,则需要通过诱导公式转化成\(\cos\)函数的形式
- 若有符号为负的\(\cos\)项,则需要通过三角公式转为正项的\(\cos\)函数进行分析
- 当指数形式的傅里叶级数系数为非零实数时:
- 相位只有0(对应正系数)和\(\pi\)(对应负系数)两种情况
- 相位为\(0,\pi\)时,复数展开为三角形式的\(j\sin \theta\)项为0
- 此时的幅度谱和相位谱可以用同一个频谱图表示,正谱线代表0相位,负谱线代表\(\pi\)相位
这一块不是很懂
例
已知某一个周期信号的傅里叶级数展开式为:
\[f(t)=1-\frac{1}{2}\cos\left( \frac{\pi}{4}t- \frac{2\pi}{3} \right)+\frac{1}{4}\sin\left( \frac{\pi}{3}t- \frac{\pi}{6} \right)
\]
试求基波角频率\(\Omega\),谐波的次数
\[\begin{align}
&\omega_{1}=\frac{\pi}{4}\quad \omega_{2}=\frac{\pi}{3}\implies T_{1}=8\quad T_{2}=6\\ \\
&\therefore T=lcm(T_{1},T_{2})=24\quad \Omega=\frac{2\pi}{T}=\frac{\pi}{12}\\ \\
&f(t)=1-\frac{1}{2}\cos\left( \frac{\pi}{4}t+ \frac{\pi}{3}-\pi \right)+\frac{1}{4}\sin\left( \frac{\pi}{3}t- \frac{2\pi}{3}+ \frac{\pi}{2} \right)\\ \\
&=1+\frac{1}{2}\cos\left( \frac{\pi}{4}t+ \frac{\pi}{3} \right)+\frac{1}{4}\cos\left( \frac{\pi}{3}t - \frac{2\pi}{3}\right)\\ \\
&=1+\frac{1}{2}\cos\left( 3\Omega t+\frac{\pi}{3} \right)+\frac{1}{4}\cos\left( 4\Omega t- \frac{2\pi}{3} \right)\\ \\
& \frac{A_{0}}{2}=1\ ,\ A_{3}=\frac{1}{2}\ ,\ \varphi_{3}=\frac{\pi}{3}\ ,\ A_{4}=\frac{1}{4}\ ,\ \varphi_{4}=-\frac{2\pi}{3}\\ \\
&谐波的次数为3,4
\end{align}
\]
周期信号频谱的特点
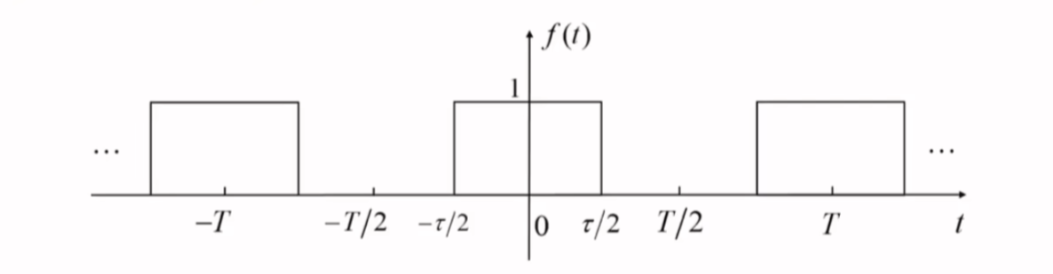
以周期矩形脉冲信号为例讨论周期信号频谱的特点:
\[\begin{align}
F_{n}&=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\Omega t}dt=\frac{1}{T}\int_{-\frac{\tau}{2}}^{\frac{\tau}{2}}e^{-jn\Omega t}dt\\ \\
&=\frac{1}{T}\cdot \frac{1}{-jn\Omega}e^{-jn\Omega t}\bigg|_{-\frac{\tau}{2}}^{\frac{\tau}{2}}=\frac{2}{T}\cdot \frac{1}{2jn\Omega}\left( e^{jn\Omega\frac{\tau}{2}}-e^{-jn\Omega \frac{\tau}{2}} \right)\\ \\
&而 \sin \theta= \frac{e^{j\theta}-e^{-j\theta}}{2j}:\\ \\
原式&=\frac{2}{Tn\Omega}\sin \left( n\Omega \frac{\tau}{2} \right)=\frac{2}{Tn\Omega}\cdot \frac{\sin\left( n\Omega \frac{\tau}{2} \right)}{n\Omega \frac{\tau}{2}}\cdot n\Omega \frac{\tau}{2}\\ \\
&而 Sa(t)= \frac{\sin t}{t}: \\ \\
原式&=\frac{\tau}{T}Sa\left( n\Omega \frac{\tau}{2} \right)
\end{align}
\]
结论:
\[F_{n}=\frac{\tau}{T}Sa\left( n\Omega \frac{\tau}{2} \right)
\]
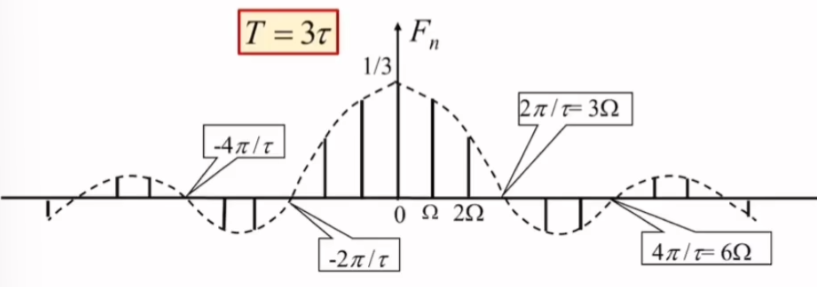
寻找频谱的过零点:
- 由于频谱函数为定义域离散的\(Sa\)函数\(Sa(t)=\frac{\sin t}{t}\),所以函数分子中的\(\sin\)为0时即为函数的零点
- 令\(n\Omega \frac{\tau}{2}=\pm m\pi\ (m=1,2,\dots)\)
- 过零点:\(n\Omega=\pm \frac{2m\pi}{\tau}\)
- 当\(T=k\tau\)时,\(n\Omega=m\cdot k\Omega\),过零点为\(\pm k\Omega,\pm 2k\Omega, \dots\)
周期信号频谱的性质
- 离散性:
- 谱线只出现在\(\omega=0,\Omega,2\Omega, \dots\)的离散频率点上,谱线最小间隔为\(\Omega\),为离散谱
- 谐波性:
- 周期信号所含频率分量的频率均为信号角频率\(\Omega\),即 基波角频率的整数倍
- 收敛性:
- 谐波分量幅度随着\(n\)的增大而减小,\(n\to \infty\)时,\(F_{n}\to 0\)
其他周期信号的频谱也具有这三个性质
周期信号的有效频带宽度(带宽)
带宽: 离散频谱的第一过零点带宽,有两种表示形式:
\[B_{\omega}=\frac{2\pi}{\tau}(rad/s) \quad B_{f}=\frac{1}{\tau}(Hz)
\]
- 信号的有效带宽内集中了信号绝大部分的谐波能量,若丢失有效 带宽之外的谐波成分,对信号影响不明显
- 脉冲时域宽度\(\tau\)越小,传输速率越高,但同时所需要的带宽\(B_{\omega}\)越大,是一对矛盾
脉冲宽度与信号周期对频谱的影响
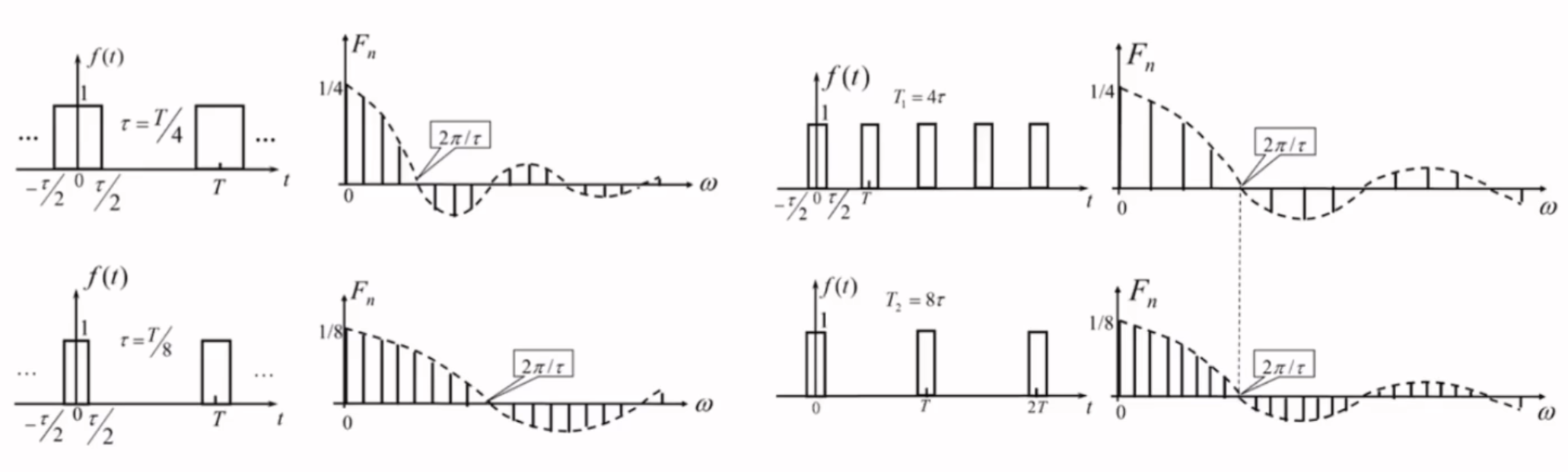
- \(T\)不变,\(\tau\)变:
- \(T\)相同,谱线的间隔不变
- 由于\(B_{\omega}=\frac{2\pi}{\tau}\),\(\tau\)越小,带宽越大,第一个过零点的频率越高
- \(\tau\)不变,\(T\)变:
- \(\tau\)不变,\(B_{\omega}\)不变,第一过零点频率不变
- 由于\(\Omega=\frac{2\pi}{T}\),\(T\)越小,\(\Omega\)越大,谱线的间隔越大
总而言之:
\[\begin{align}
B_{\omega}&\propto \frac{1}{\tau}\\ \\
\Omega &\propto \frac{1}{T}
\end{align}
\]
- 注意:当周期无限大时,谱线无限密集,幅度无限小,需要用密度来描述
周期信号的功率
\[\begin{align}
&三角级数:P=\left( \frac{A_{0}}{2} \right)^{2}+\sum_{n=1}^{\infty} \frac{A_{n}^{2}}{2}\\ \\
&指数级数:P=|F_{0}|^{2}+2\sum_{n=1}^{\infty}|F_{n}|^{2}=\sum_{n=-\infty}^{\infty}|F_{n}|^{2}
\end{align}
\]
- 对于任意余弦信号的功率的有效值,都等于\(\frac{A_{n}}{\sqrt{ 2 }}\),\(P=I^{2}Rt=I^{2}\)
- 上述两个功率的表达式称为功率信号的帕斯瓦尔\(Parseval\)恒等式,说明了周期信号平均功率和信号频谱中各个分量功率的关系
周期信号功率谱
- 对于不同的频率分量,\(|F_{n}|^{2}\)或\(\frac{A_{n}^{2}}{2}\)随离散频率\(n\Omega\)分布的特性称为周期信号的功率谱
例
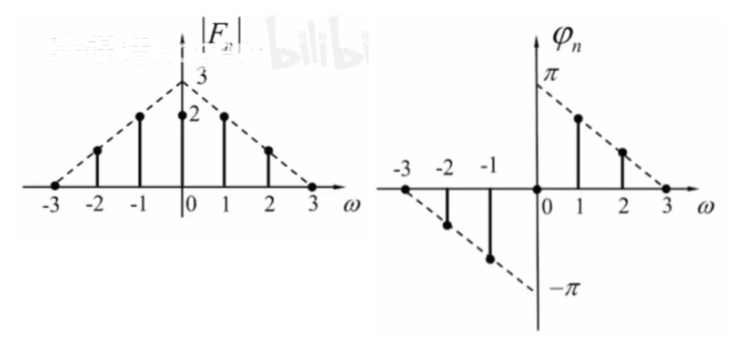
已知周期信号\(f(t)\)的双边频谱如图所示,写出\(f(t)\)指数以及三角形式的傅里叶级数
\[\begin{align}
&由图可知:\\ \\
&F_{n}\sim\left\{
\begin{array}{c}
-2&-1&0&1&2\ \\
e^{-j \frac{\pi}{3}} &2e^{-j \frac{2\pi}{3}}&2&2e^{j \frac{2\pi}{3}}&e^{j \frac{\pi}{3}}
\end{array}
\right\}\\ \\
&而f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}\quad 且由图知:间隔\Omega=1\\ \\
&\therefore f(t)=2+2e^{j\left( t+ \frac{2\pi}{3} \right)}+2e^{-j\left( t+ \frac{2\pi}{3} \right)}+e^{j\left( 2t+ \frac{\pi}{3} \right)}+e^{-j\left( 2t+ \frac{\pi}{3} \right)}\quad 即为指数形式\\ \\
&由\sin \theta= \frac{e^{j\theta}+e^{-j\theta}}{2}:\\ \\
&f(t)=2+4\cos\left( t+ \frac{2\pi}{3} \right)+2\cos\left( 2t+\frac{\pi}{3} \right)\quad 即为三角形式
\end{align}
\]
- 在写出指数形式之后,由于其对称性可以利用欧拉公式快速写出三角形式
3.3 连续时间信号的傅里叶变换
傅里叶变换的定义
频谱密度的引入
- 对于周期信号而言,信号周期\(T\)越大,频谱谱线越密集,幅度减小
- 信号周期\(T\)无限大时,周期信号变为非周期信号,谱线无限密集,幅度无穷小,离散谱过度为连续谱,需要改用密度描述频谱特性
傅里叶正变换
已知:
\[F_{n}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\Omega t}dt
\]
当\(T\to \infty\):
- \(\Omega\to d\omega\),频谱间隔无限密集,变为无穷小量
- \(n\Omega\to \omega\),离散频率\(\to\)连续频率
频谱密度:单位频率的信号频谱值
\[F(j\omega)=\lim_{ T \to \infty } \frac{F_{n}}{f} =\lim_{ T \to \infty } \int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\Omega t}dt=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt
\]
\[傅里叶正变换:F(j\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt
\]
傅里叶反变换
已知:
\[f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}=\frac{1}{T}\sum_{n=-\infty}^{\infty}F_{n}Te^{jn\Omega t}
\]
当\(T\to \infty\)时:
- \(\Omega\to d\omega\),频谱间隔无限密集,变为无穷小量
- \(n\Omega\to \omega\),离散频率\(\to\)连续频率
- \(\lim_{ T \to \infty }F_{n}T=F(j\omega)\)
- \(\frac{1}{T}=\frac{\Omega}{2\pi}\to \frac{d\omega}{2\pi}\)
则:
\[傅里叶反变换:f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}d\omega
\]
傅里叶变换对
\[f(t) \leftrightarrow F(j\omega)
\]
\[\begin{align}
&傅里叶正变换:F(j\omega)=\mathcal{F}[f(t)]\\ \\
&傅里叶反变换: f(t)=\mathcal{F}^{-1}[F(j\omega)]
\end{align}
\]
傅里叶变换存在的充分条件
\[信号满足绝对可积条件:\int_{-\infty}^{+\infty}|f(t)|dt<\infty \implies傅里叶变换存在
\]
- 注意此处为充分条件,傅里叶变换存在不一定信号绝对可积
- 阶跃信号\(\varepsilon(t)\)的广义傅里叶变换存在,但不满足绝对可积
常用结论
\[\begin{align}
&F(0)=F(j\omega)\bigg|_{\omega=0}=\int_{-\infty}^{+\infty}f(t)dt\\ \\
&f(0)=f(t)\bigg|_{\omega=0}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega )d\omega
\end{align}
\]
频谱密度函数
信号为实函数:
\[\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt=\int_{-\infty}^{+\infty}f(t)\cos \omega tdt-j\int_{-\infty}^{+\infty}f(t)\sin \omega tdt\\ \\
&=R(\omega)+jX(\omega)
\end{align}
\]
\[\begin{cases}
R(\omega)=\int_{-\infty}^{+\infty}f(t)\cos \omega tdt\quad R(-\omega)=R(\omega)\quad 为\omega的偶函数\\ \\
X(\omega)=-\int_{-\infty}^{+\infty}f(t)\sin \omega tdt\quad X(-\omega)=-X(\omega)\quad 为\omega的奇函数
\end{cases}
\]
\[F(j\omega)=|F(j\omega)|e^{j\varphi(\omega)}
\]
其中:
\[\begin{align}
&|F(j\omega)|=\sqrt{ R^{2}(\omega)+X^{2}(\omega) }\quad |F(-\omega)|=|F(\omega)|\quad 为\omega 的偶函数,具有幅频特性\\ \\
&\varphi(\omega)=\arctan \frac{X(\omega)}{R(\omega)}\quad \varphi(-\omega)=-\varphi(\omega)\quad 为\omega的奇函数,具有相频特性
\end{align}
\]
常见信号的傅里叶变换
矩形脉冲(门函数)
\[g_{\tau}(t)=\left[ \varepsilon\left( t+ \frac{\tau}{2} \right) -\varepsilon\left( t- \frac{\tau}{2} \right)\right]=\begin{cases}
1\quad|t|\leq \frac{\tau}{2}\\ \\
0\quad |t|> \frac{\tau}{2}
\end{cases}
\]
门函数傅里叶变换推导:
\[\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt=\int_{-\frac{\tau}{2}}^{ \frac{\tau}{2}}e^{-j\omega t}dt=\frac{1}{-j\omega}e^{-j\omega t}\bigg|_{-\frac{\tau}{2}}^{\frac{\tau}{2}}\\ \\
&= \frac{2\left( e^{j\omega \frac{\tau}{2}}-e^{-j\omega \frac{\tau}{2}} \right)}{2j\omega}=\frac{2}{\omega}\sin \frac{\omega \tau}{2}\\ \\
&=\frac{2}{\omega}\cdot \frac{\sin \frac{\omega \tau}{2}}{ \frac{\omega \tau}{2}}\cdot \frac{\omega \tau}{2}=\tau Sa\left( \frac{\omega \tau}{2} \right)
\end{align}
\]
结论:
\[g_{\tau}(t)\leftrightarrow \tau Sa\left( \frac{\omega \tau}{2} \right)
\]
-
该频谱为实频谱,实频谱的幅度、相位合二为一
-
有效带宽通过第一过零点可知\(B_{\omega}= \frac{2\pi}{\tau}(rad/s)\)
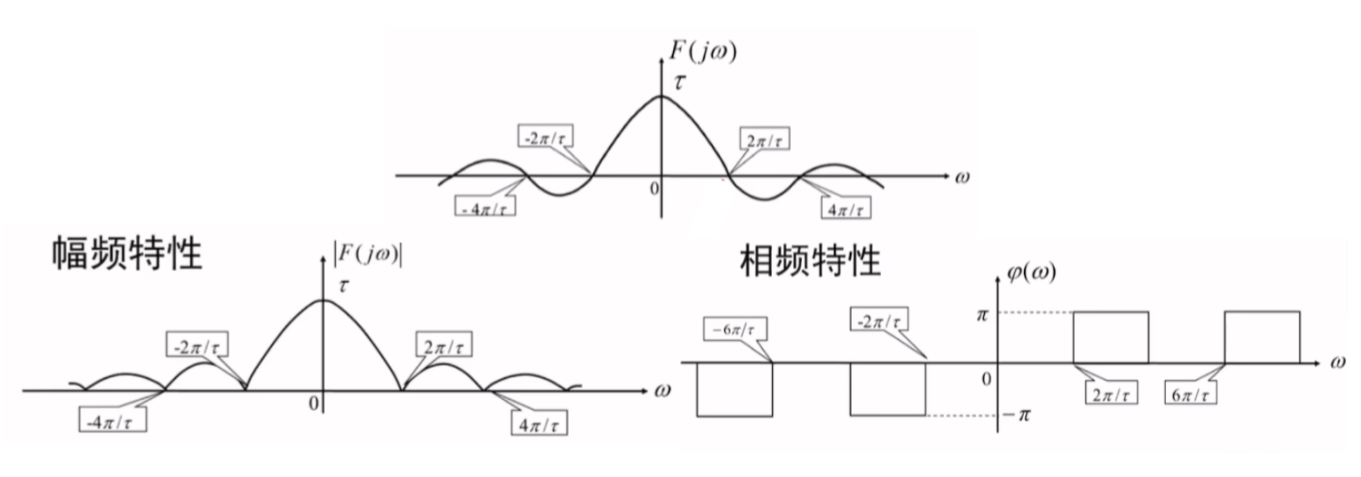
-
由于频谱为实频谱,幅频特性只需要取绝对值即可
-
由于频谱为实频谱,相频特性只会出现\(-\pi,0,\pi\),分别对应\(\cos \theta=\{ -1,1 \}\),即频谱密度为正时相频为\(0\),频谱密度为负时相频为\(\pi\),负半轴通过原点对称可得\(\pi\to-\pi\)
特殊结论:
时域有限的信号,频域上无限展宽
不知道啥意思
单边指数信号
\[f(t)=e^{\alpha t}\varepsilon(t)=\begin{cases}
e^{-\alpha t}\quad t\geq 0\\ \\
0\quad t< 0
\end{cases}(\alpha>0)
\]
单边指数函数傅里叶变换推导:
\[\begin{align}
F(j\omega)&=\int_{0}^{+\infty}e^{-\alpha t}\cdot e^{-j\omega t}dt=\int_{0}^{+\infty}e^{-(\alpha+j\omega)t}dt\\ \\
&=\frac{1}{-(\alpha+j\omega)}e^{-(\alpha+j\omega)t}\bigg|_{0}^{+\infty}=\frac{1}{\alpha+j\omega}
\end{align}
\]
结论:
\[e^{\alpha t}\varepsilon(t)\leftrightarrow \frac{1}{\alpha+j\omega}
\]
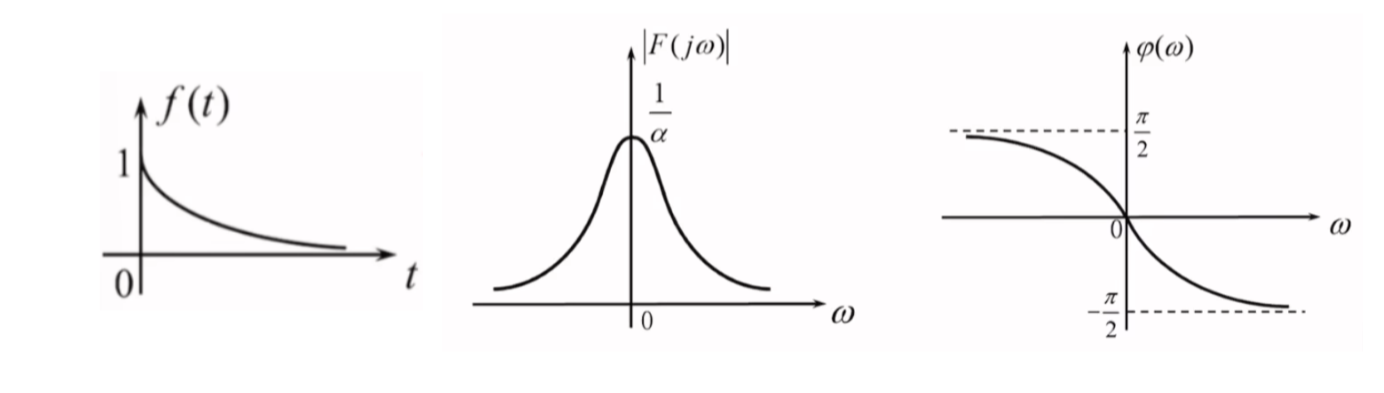
幅频特性:
\[|F(j\omega)|=\left| \frac{1}{\alpha+j\omega} \right|=\frac{1}{|\alpha+j\omega|}=\frac{1}{\sqrt{ \alpha^{2}+\omega^{2} }}
\]
相频特性:
\[\varphi(\omega)=\angle \frac{1}{\alpha+j\omega}=\angle 1-\angle(\alpha+j\omega)=0{\degree}-\arctan \frac{\omega}{\alpha}=-\arctan \frac{\omega}{\alpha}
\]
偶双边指数信号
\[f(t)=e^{-\alpha |t|}=\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
e^{\alpha t}\quad t<0
\end{cases}\quad(\alpha>0)
\]
偶双边指数函数傅里叶变换推导:
\[\begin{align}
F(j\omega)&=\int_{-\infty}^{0}e^{\alpha t}\cdot e^{-j\omega t}dt+\int_{0}^{+\infty}e^{-\alpha t}\cdot e^{-j\omega t}dt\\ \\
&=\int_{-\infty}^{0}e^{(\alpha-j\omega )t}dt+\int_{0}^{+\infty}e^{-(\alpha+j\omega)t}dt\\ \\
&=\frac{1}{\alpha-j\omega}e^{(\alpha-j\omega)t}\bigg|_{-\infty}^{0}+ \frac{1}{-(\alpha+j\omega )}e^{-(\alpha+j\omega)t}\bigg|_{0}^{+\infty}\\ \\
&=\frac{1}{\alpha-j\omega}+\frac{1}{\alpha+j\omega}= \frac{2\alpha}{\alpha^{2}+\omega^{2}}
\end{align}
\]
结论:
\[e^{-\alpha |t|}\leftrightarrow \frac{2\alpha}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)
\]
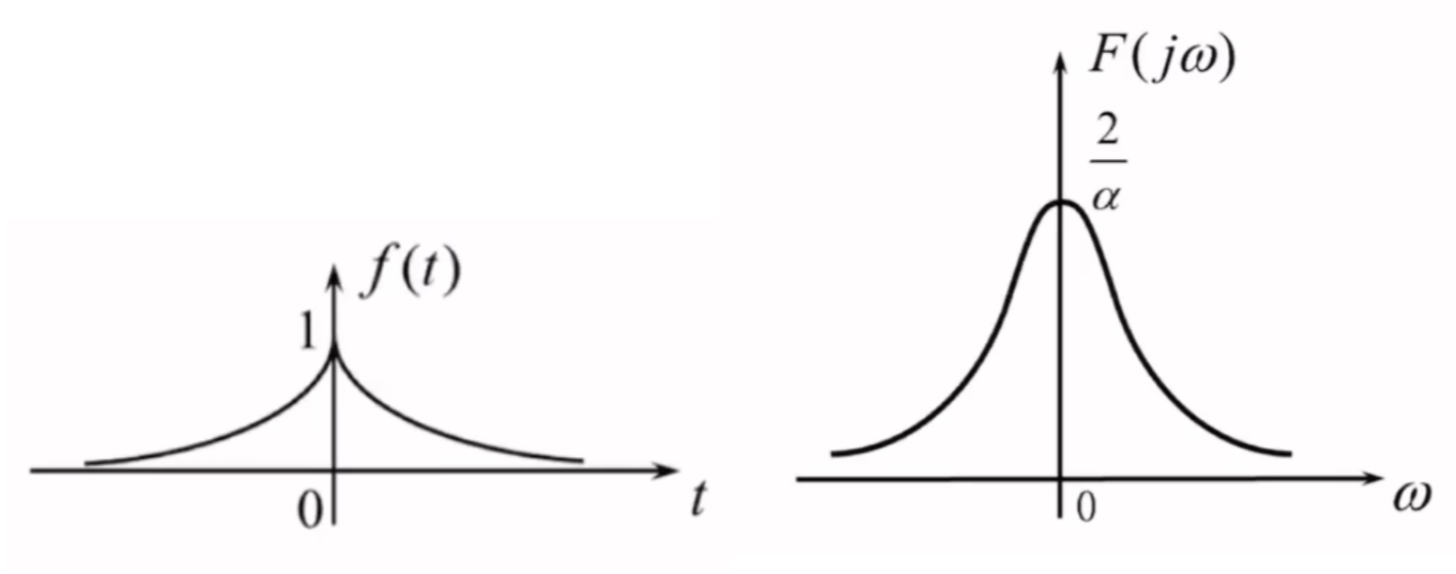
幅频特性:
- 由于频谱为实频谱,幅频特性直接取绝对值
- \(|F(j\omega)|= \frac{2\alpha}{\alpha^{2}+\omega^{2}}\)
相频特性:
- 由于频谱为恒正的实频谱,相位恒为0
- \(\varphi(\omega)=0\)
奇双边指数信号
\[f(t)=\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t }\quad t< 0
\end{cases}\quad (\alpha>0)
\]
奇双边指数函数傅里叶变换推导:
\[\begin{align}
F(j\omega)&=-\int_{-\infty}^{0}e^{\alpha t}\cdot e^{-j\omega t}dt+\int_{0}^{+\infty}e^{-\alpha t}\cdot t e^{-j\omega t}dt\\ \\
&=\frac{1}{\alpha+j\omega}-\frac{1}{\alpha-j\omega}= \frac{-j \cdot2\omega}{\alpha^{2}+\omega^{2}}
\end{align}
\]
结论:
\[\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t }\quad t< 0
\end{cases}
\leftrightarrow \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)
\]
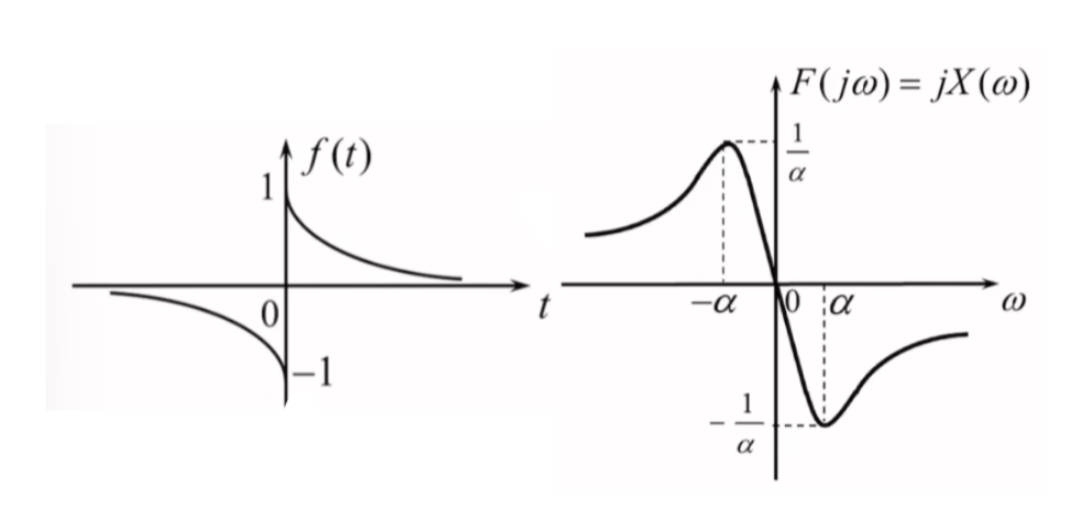
幅频特性:
- 由于频谱为虚频谱,幅频特性即为频谱去掉虚数单位后取绝对值
- \(|F(j\omega)|= \frac{2|\omega|}{\alpha^{2}+\omega^{2}}\)
相频特性:
- 由于频谱为虚频谱,三角展开为\(j\sin \theta\),则相频取\(\theta=\left\{ -\frac{\pi}{2} ,\frac{\pi}{2} \right\}\)对应着频谱取\(\{ -j,j \}\)
\[\varphi(\omega)=\begin{cases}
\frac{\pi}{2}\quad \omega<0\\ \\
-\frac{\pi}{2}\quad \omega>0
\end{cases}
\]
冲激信号及其导数
*傅里叶变换的时域微分性质
设函数\(f(t)\)的傅里叶变换为\(F(\omega)\):
\[\mathcal{F}\{ f(t) \}=F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt
\]
且\(f(t)\)及其各阶导数绝对可积,则有:
\[\mathcal{F}\{ f^{(n)}(t) \}=(j\omega)^{n}F(\omega)
\]
推导关键在于:
- \(\int_{-\infty}^{+\infty}f(t)dt<\infty\implies \lim_{ t \to \infty }f(t)=0\)
- 对原积分采用分部积分,常数项为\(f^{(n-1)}(t)e^{-j\omega t}\bigg|_{-\infty}^{+\infty}=0\)
- 可以得到递推\(\int_{-\infty}^{+\infty}f^{(n)}(t)e^{-j\omega t}dt=(j\omega )\int_{-\infty}^{+\infty}f^{(n-1)}(t)e^{-j\omega t}dt\)
冲激信号傅里叶变换推导:
\[\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty }\delta(t)e^{-j\omega t}dt=e^{-j\omega t}\bigg|_{t=0}=1\\ \\
即:\quad&\delta(t)\leftrightarrow 1
\end{align}
\]
\[\begin{align}
&由于\mathcal{F}\{ f^{(n)}(t) \}=(j\omega)^{n}\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt:\\ \\
&\mathcal{F}\{ \delta^{(n)}(t) \}=(j\omega)^{n}\int_{-\infty}^{+\infty}\delta(t)e^{-j\omega t}dt=(j\omega)^{n}\\ \\
&即:\quad \delta^{(n)}(t)\leftrightarrow (j\omega)^{n}
\end{align}
\]
直流信号\(f(t)=A\)
直流信号傅里叶变换推导过程:
\[\begin{align}
&\mathcal{F}^{-1}\{ \delta(\omega) \}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\delta(\omega)e^{j\omega t}d\omega=\frac{1}{2\pi}e^{j\omega t}\bigg|_{\omega=0}=\frac{1}{2\pi}\\ \\
&则: \frac{1}{2\pi}\leftrightarrow \delta(\omega)\implies 1\leftrightarrow 2\pi \delta(\omega)\implies A\leftrightarrow 2\pi A\delta(\omega)
\end{align}
\]
- 直流信号的傅里叶变换的推导过程借助了反傅里叶变换逆推而来
- 常数函数\(f(t)=A\)的傅里叶变换为\(2\pi A\delta(\omega)\),然而\(\int_{-\infty}^{+\infty}f(t)dt=\infty\)并不是绝对可积,这再次印证绝对可积是傅里叶变换的充分条件
- 冲激信号和常数的时、频特性存在对称性
- 冲激信号的傅里叶变换为常数\(\delta(t)\leftrightarrow 1\)
- 常数的傅里叶变换为冲激信号\(1\leftrightarrow 2\pi\delta(\omega)\)
符号函数
\[sgn(t)=\begin{cases}
-1\quad t<0\\ \\
1\quad t>0
\end{cases}
\]
符号函数傅里叶变换推导过程:
\[\begin{align}
&设f_{\alpha}(t)=\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t}\quad t<0
\end{cases}\quad (\alpha>0)\\ \\
&则f_{\alpha}(t)\leftrightarrow \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)\\ \\
&而sgn(t)=\lim_{ \alpha \to 0 }f_{\alpha}(t) \\ \\
&则sgn(t)\xleftrightarrow{广义傅里叶变换}\lim_{ \alpha \to 0 } \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}=\frac{2}{j\omega}
\end{align}
\]
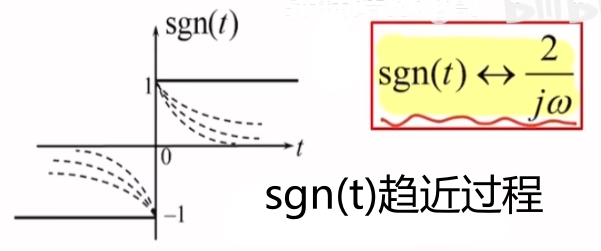
推导关键:
- 利用了奇双边指数信号在\(\alpha\to 0\)时趋近于\(sgn(t)\)的特性进行推导
- \(sgn(t)\leftrightarrow \frac{2}{j\omega}\)在广义傅里叶变换下成立
阶跃函数
\[\varepsilon(t)=\begin{cases}
1\quad t>0\\ \\
0\quad t<0
\end{cases}
\]
阶跃函数傅里叶变换推导过程:
\[\begin{align}
&由\varepsilon(t)=\frac{1}{2}+\frac{1}{2}sgn(t):\\ \\
&\varepsilon(t)\xleftrightarrow{广义傅里叶变换}\pi \delta(\omega)+ \frac{1}{j\omega}
\end{align}
\]
- 利用\(\varepsilon(t)\)与符号函数的关系从而得到傅里叶变换
总结
\[\begin{align}
&傅里叶正变换:F(j\omega)=\mathcal{F}\{ f(t) \}=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt\\ \\
&傅里叶反变换:f(t)=\mathcal{F}^{-1}\{ F(j\omega) \}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}d\omega\\ \\
& 时域t\xrightleftharpoons[\text{傅里叶反变换}]{\text{傅里叶正变换}}频域\omega
\end{align}
\]
\[\begin{align}
&门函数:g_{\tau}(t)\leftrightarrow \tau Sa\left( \frac{\omega \tau}{2} \right)\\ \\
&单边指数信号:e^{-\alpha t}\varepsilon(t)\leftrightarrow \frac{1}{\alpha+j\omega}\quad (\alpha>0)\\ \\
&偶双边指数信号:e^{-\alpha |t|}\leftrightarrow \frac{2\alpha}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)\\ \\
&奇双边指数信号:\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t}\quad t<0
\end{cases}\leftrightarrow \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)\\ \\
&冲激信号及其导数: \begin{cases}
\delta(t)\leftrightarrow 1\\ \\
\delta^{(n)}(t)\leftrightarrow (j\omega)^{n}
\end{cases}\\ \\
&直流信号:1\leftrightarrow 2\pi \delta(\omega)\\ \\
&符号函数:sgn(t)\leftrightarrow \frac{2}{j\omega}\\ \\
&阶跃函数: \varepsilon(t)=\frac{1}{2}+\frac{1}{2}sgn(n)\leftrightarrow \pi \delta(\omega)+ \frac{1}{j\omega}
\end{align}
\]
3.4 傅里叶变换的性质
线性性质
\[\begin{align}
&已知:f_{1}(t)\leftrightarrow F_{1}(j\omega)\quad f_{2}(t)\leftrightarrow F_{2}(j\omega)\\ \\
&则有:af_{1}(t)+bf_{2}(t)\leftrightarrow aF_{1}(t)+bF_{2}(t)
\end{align}
\]
- 线性性质是傅里叶变换最基本的性质
- 傅里叶变换是线性变换
例
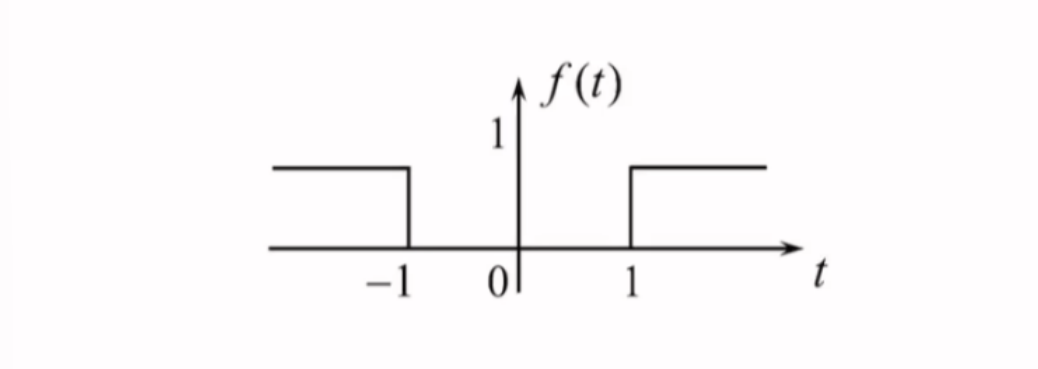
求图示信号\(f(t)\)的傅里叶变换
\[\begin{align}
&观察可知f(t)=1-g_{2}(t)\\ \\
&则f(t)=1-g_{2}(t)\leftrightarrow 2\pi \delta(\omega)-2Sa(\omega)
\end{align}
\]
奇偶性
\[\begin{align}
&若f(t)\leftrightarrow F(j\omega)\\ \\
&则:f(-t)\leftrightarrow F(-j\omega)
\end{align}
\]
实信号\(f(t)\)
\[\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt=\int_{-\infty}^{+\infty}f(t)cod\omega tdt-j\int_{-\infty}^{+\infty}f(t)\sin \omega tdt\\ \\
&=R(\omega)+jX(\omega)\\ \\
其中 :&\begin{cases}
R(-\omega)=R(\omega)\ 为偶函数\\ \\
X(-\omega)=-X(\omega)\ 为奇函数
\end{cases}
\end{align}
\]
若\(f(t)\)为偶函数:
\[\begin{align}
&X(\omega)=-\int_{-\infty}^{+\infty}f(t)\sin \omega tdt=0\\ \\
&F(j\omega)=\int_{-\infty}^{+\infty}f(t)\cos \omega tdt=R(\omega)
\end{align}
\]
若\(f(t)\)为奇函数:
\[\begin{align}
&R(\omega)=\int_{-\infty}^{+\infty}f(t)\cos \omega tdt=0\\ \\
&F(j\omega)=-j\int_{-\infty}^{+\infty}f(t)\sin \omega tdt=jX(\omega)
\end{align}
\]
虚信号\(f(t)=j\cdot g(t)\)
\[\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty}j\cdot g(t)e^{-j\omega t}dt=\int_{-\infty}^{+\infty}g(t)\sin \omega tdt+j\int_{-\infty}^{+\infty}g(t)\cos \omega tdt\\ \\
&=R(\omega)+j\cdot X(\omega)\\ \\
其中:&\begin{cases}
R(\omega)=\int_{-\infty}^{+\infty}g(t)\sin \omega tdt\quad R(-\omega)=-R(\omega)\quad 为\omega 的奇函数\\ \\
X(\omega)=\int_{-\infty}^{+\infty}g(t)\cos \omega tdt\quad X(-\omega)=X(\omega)\quad 为\omega的偶函数
\end{cases}
\end{align}
\]
\(f(t)\)为偶函数
\[R(\omega)=\int_{-\infty}^{+\infty}g(t)\sin \omega tdt=0\quad F(j\omega)=j\int_{-\infty}^{+\infty}g(t)\cos \omega tdt=j\cdot X(\omega)
\]
\(f(t)\)为奇函数
\[X(\omega)=\int_{-\infty}^{+\infty}g(t)\cos \omega tdt=0\quad F(j\omega)=\int_{-\infty}^{+\infty}g(t)\sin \omega tdt=R(\omega)
\]
实信号的奇偶分量的频谱
\[\begin{align}
&f(t)\leftrightarrow F(j\omega)=R(\omega)+j\cdot X(\omega)\\ \\
&f(-t)\leftrightarrow F(-j\omega)=F^{*}(j\omega)
\end{align}
\]
\[\begin{align}
&f_{ev}(t)= \frac{f(t)+f(-t)}{2}\leftrightarrow \mathrm{Re}[F(j\omega)]=R(\omega)\\ \\
&f_{od}(t)= \frac{f(t)-f(-t)}{2}\leftrightarrow j\cdot \mathrm{Im}[F(j\omega)]=j\cdot X(\omega)
\end{align}
\]
- 其中,\(\mathrm{Re}(x)\)为复数\(x\)的实部,\(\mathrm{Im}(x)\)为复数\(x\)的虚部
时移性质\(f(t+t_{0})\)
\[f(t)\leftrightarrow F(j\omega)\quad 则:f(t\pm t_{0})\leftrightarrow F(j\omega)e^{\pm \omega t_{0}}
\]
- 信号时移引起频域附加线性相位,幅度不变
- 信号左移\(t_{0}\):\(f(t)\to f(t+t_{0})\),相位超前\(w_{}t_{0}\),函数乘\(e^{j\omega t_{0}}\)
- 信号右移\(t_{0}\):\(f(t)\to f(t-t_{0})\),相位之后\(\omega t_{0}\),函数乘\(e^{-j\omega t_{0}}\)
例
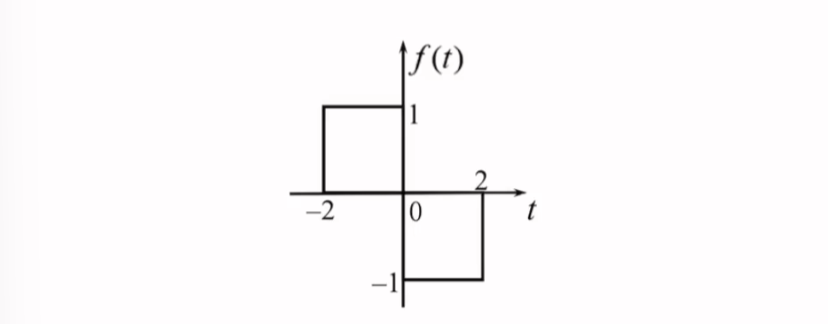
请求图示信号\(f(t)\)的傅里叶变换
\[\begin{align}
解:&\\ \\
&观察可知f(t)=g_{2}(t+1)-g_{2}(t-1)\\ \\
&由于g_{\tau}(t)\leftrightarrow \tau Sa\left( \frac{\tau \omega}{2} \right)\\ \\
&g_{2}(t+1)-g_{2}(t-1)\leftrightarrow 2Sa(\omega)e^{j\omega}-2Sa(\omega)e^{-j\omega}\\ \\
&而 \frac{e^{j\omega}-e^{-j\omega}}{2}=j\cdot \sin \omega\\ \\
&\therefore f(t)\leftrightarrow 4j\cdot Sa(\omega)\sin \omega
\end{align}
\]
频移性质\(F(j(\omega\mp \omega_{0}))\)
\[f(t)\leftrightarrow F(j\omega)\quad 则:f(t)e^{\pm j\omega_{0}t}\leftrightarrow F[j(\omega\mp \omega_{0})]
\]
\[\begin{align}
&f(t)\to f(t)e^{j\omega_{0}t}\quad F(j\omega)\to F[j(\omega-\omega_{0})]\quad 信号频谱右移\omega_{0}\\ \\
&f(t)\to f(t)e^{-j\omega_{0}t}\quad F(j\omega)\to F[j(\omega+\omega_{0})]\quad 信号频谱左移\omega_{0}
\end{align}
\]
重要结论:
\[e^{j\omega_{0}t}\leftrightarrow {2}\pi \delta(\omega-\omega_{0})\quad e^{-j\omega_{0}t}\leftrightarrow {2}\pi \delta(\omega+\omega_{0})
\]
\[\begin{align}
&\cos \omega_{0}t=\frac{1}{2}[e^{j\omega_{0}t}+e^{-j\omega_{0}t}]\implies \cos \omega_{0}t\leftrightarrow \pi[\delta(\omega+\omega_{0})+\delta(\omega-\omega_{0})] \\ \\
&\sin \omega_{0}t=\frac{1}{2j}[e^{j\omega_{0}t}-e^{-j\omega_{0}t}]\implies \sin \omega_{0}t\leftrightarrow j\cdot \pi[\delta(\omega+\omega_{0})-\delta(\omega-\omega_{0})]
\end{align}
\]
调制
\[\begin{align}
&f(t)\cos \omega_{0}t=f(t)\cdot \frac{1}{2}[e^{j\omega_{0}t}+e^{-j\omega_{0}t}]\leftrightarrow \frac{1}{2}\{ F[j(\omega+\omega_{0})]+F[j(\omega-\omega_{0})] \}\\ \\
&f(t)\sin \omega_{0}t=f(t)\cdot \frac{1}{2j}[e^{j\omega_{0}t}-e^{-j\omega_{0}t}]=\frac{j}{2}\{ F[j(\omega+\omega_{0})]-F[j(\omega-\omega_{0})] \}
\end{align}
\]
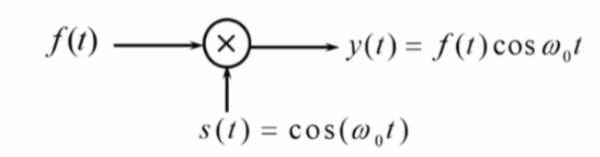
其中:
\[\begin{cases}
f(t):调制信号(含信息 )\\ \\
s(t):载波信号(单一高频率信号)\\ \\
y(t):已调信号
\end{cases}
\]
时域调制:
- 原函数\(f(t)\)将作为调制后的包络线
- 调制后的函数将会变为震荡
频域频谱搬移:
- 频域将会减半后搬移到两个冲激信号处
尺度变换性质
\[\begin{align}
&若f(t)\leftrightarrow F(j\omega)\quad 则:f(at)\leftrightarrow \frac{1}{|a|}F\left( j\cdot \frac{\omega}{a} \right),a\neq 0,a\in R
\end{align}
\]
- 可以类比\(\delta(t)\)的尺度变换性质:\(\delta(at+t_{0})= \frac{1}{|a|}\delta\left( t+ \frac{t_{0}}{a} \right)\)
- 特别地,若\(a=-1\),则\(f(-t)\leftrightarrow F(-j\omega)\),称为时间倒置定理
总结
\[e^{j\omega_{0}t}f(at+b)\leftrightarrow \frac{1}{|a|}F\left( j\cdot \frac{\omega-\omega_{0}}{a} \right)e^{j\cdot \frac{\omega-\omega_{0}}{a}\cdot b}
\]
- 时域内对单独的\(t\)变化
- 频域内对单独的\(\omega\)变化
例
求\(f(t)=3e^{-(3+2j)t}\varepsilon(t+1)\)的傅里叶变换
\[\begin{align}
解:&\\ \\
f(t)&=3\cdot e^{-2jt}\cdot e^{-3t}\varepsilon(t+1)\\ \\
&=3e^{3}\cdot e^{-2jt}\cdot e^{-3(t+1)}\varepsilon(t+1)\\ \\
&\begin{array}{r}
e^{-3t}\varepsilon(t)&\leftrightarrow & \frac{1}{j\omega+3} \\
e^{-3(t+1)}\varepsilon(t+1)&\leftrightarrow & \frac{e^{j\omega}}{j\omega+3} \\
e^{-2jt}\cdot e^{-3(t+1)}\varepsilon(t+1)&\leftrightarrow & \frac{e^{j(\omega+2)}}{j(\omega+2)+3} \\
3e^{3}\cdot e^{-2jt}\cdot e^{-3(t+1)}\varepsilon(t+1) &\leftrightarrow & \frac{e^{3}\cdot e^{j(\omega+2)}}{j(\omega+2)+3}
\end{array}
\end{align}
\]
傅里叶变换的性质 II
对称性
\[\begin{align}
若:f(t)&\leftrightarrow F(j\omega)\\ \\
则:F(jt)&\leftrightarrow 2\pi f(-\omega)
\end{align}
\]
推导:
\[\begin{align}
&若f(t)\leftrightarrow F(j\omega)\\ \\
&则:f(t)= \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{-j\omega t}d\omega\\ \\
&\implies {2}\pi f(-t)=\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}d\omega\\ \\
&\implies 2\pi f(-\omega)=\int_{-\infty}^{+\infty}F(jt)e^{j\omega t}dt=\mathcal{F}\{ F(jt) \}\\ \\
&即F(jt)\leftrightarrow 2\pi f(-\omega)
\end{align}
\]
记忆:
- 交换后\(\omega\)前加符号
- 交换后\(\omega\)侧乘\(2\pi\)
特殊情况:
\[\begin{align}
\delta(t)&\leftrightarrow 1\\ \\
1&\leftrightarrow 2\pi f(-\omega)
\end{align}
\]
例
求信号\(f(t)=Sa(\omega_{0}t)= \frac{\sin \omega_{0}t}{\omega_{0}t}\)的傅里叶变换
\[\begin{align}
g_{\tau}(t)&\leftrightarrow \tau Sa\left( \omega \cdot\frac{\tau}{2} \right)\\ \\
g_{2\tau}(t)&\leftrightarrow 2\tau Sa(\omega \tau)\\ \\
g_{2\omega_{0}}(t)&\leftrightarrow 2\omega_{0}Sa(\omega \omega_{0})\\ \\
2\pi g_{2\omega_{0}}(-\omega)&\leftrightarrow 2\omega_{0}Sa(\omega_{0}t)\\ \\
Sa(\omega_{0}t)&\leftrightarrow \frac{\pi}{\omega_{0}}g_{2\omega_{0}}(\omega)\quad(g(t)为偶函数)
\end{align}
\]
求频谱\(F(j\omega)=2\pi e^{2\omega}\varepsilon(-\omega)\)的傅里叶反变换
\[\begin{align}
e^{-2t}\varepsilon(t)&\leftrightarrow \frac{1}{2+j\omega}\\ \\
\frac{1}{2+jt}&\leftrightarrow 2\pi e^{-2(-\omega)}\varepsilon(-\omega)=2\pi e^{2\omega}e(-\omega)\\ \\
&\therefore f(t)=\frac{1}{2+jt}
\end{align}
\]
技巧:
- 在求傅里叶变换前,可以先观察式子的次数结构
- 利用已知傅里叶变换以及对称性化简求解
时域卷积性质
\[\begin{align}
&若f_{1}(t)\leftrightarrow F_{1}(j\omega)\quad f_{2}(t)\leftrightarrow F_{2}(j\omega)\\ \\
&则:f_{1}(t)*f_{2}(t)\leftrightarrow F_{1}(j\omega)\cdot F_{2}(j\omega)
\end{align}
\]
FFT变换原理:
\[f_{1}(t)*f_{2}(t)=\mathcal{F}^{-1}\{ \mathcal{F}\{ f_{1}(t) \}\times \mathcal{F}\{ f_{2}(t) \} \}
\]
记忆:时域卷积,频域相乘
例

求图示三角波信号的傅里叶变换
三角波可以由两个门函数卷积而成:
\[\begin{align}
&Ag_{\tau}(t)*Ag_{\tau}(t)=A^{2}(\tau-t)\varepsilon(t)+A^{2}(\tau+t)\varepsilon(-t)
\end{align}
\]
\[\begin{align}
解:&\\ \\
&已知f(t)=f_{1}(t)*f_{1}(t)=\sqrt{ \frac{2}{\tau} }g_{\frac{\tau}{2}}(t)* \sqrt{ \frac{2}{\tau} }g_{\frac{\tau}{2}}(t)\\ \\
&f_{1}(t)\leftrightarrow \sqrt{ \frac{2}{\tau} }\cdot \frac{\tau}{2}Sa\left( \frac{\omega \tau}{4} \right)=\sqrt{ \frac{\tau}{2} }Sa\left( \frac{\omega \tau}{4} \right)\\ \\
&\therefore f(t)=f_{1}(t)*f_{1}(t)\leftrightarrow\frac{\tau}{2}Sa^{2}\left( \frac{\omega \tau}{4} \right)
\end{align}
\]
频域卷积性质
\[\begin{align}
&若f_{1}(t)\leftrightarrow F_{1}(j\omega)\quad f_{2}(t)\leftrightarrow F_{2}(j\omega)\\ \\
&则:f_{1}(t)\cdot f_{2}(t)\leftrightarrow \frac{1}{2\pi}[F_{1}(j\omega)*F_{2}(j\omega)]
\end{align}
\]
记忆:时域相乘,频域卷积
例
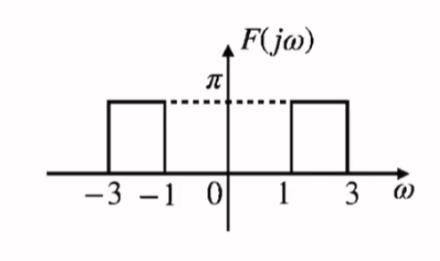
求图示频谱的傅里叶反变换
\[\begin{align}
&注意到:\\ \\
&F(j\omega)=g_{2}(\omega)*\delta(\omega-2)+g_{2}(\omega)*\delta(\omega+2)=g_{2}(\omega)*[\delta(\omega-2)+\delta(\omega+2)]\\ \\
&而:g_{2}(\omega)\leftrightarrow \frac{1}{\pi}Sa(t)\quad \cos2t\leftrightarrow \pi[\delta(\omega+2)+\delta(\omega-2)]\\ \\
&\therefore F(j\omega)= \frac{1}{2\pi}[2\pi g_{2}(\omega)]*\pi[\delta(\omega+2)+\delta(\omega-2)]\leftrightarrow \frac{1}{\pi}Sa(t)\cos 2t
\end{align}
\]
求解\(f(t)=\left( \frac{\sin t}{t} \right)^{2}\)
\[\begin{align}
&f(t)=Sa^{2}(t)\quad Sa(t)\leftrightarrow \pi g_{2}(\omega)\\ \\
&f(t)\leftrightarrow \frac{1}{2\pi}[\pi g_{2}(\omega)*\pi g_{2}(\omega)]=\frac{\pi}{2}[g_{2}(\omega)*g_{2}(\omega)]\\ \\
&画图可知卷积结果为三角波\\ \\
&f(t)\leftrightarrow(t+2)[\varepsilon(t+2)-\varepsilon(t)]+(2-t)[\varepsilon(t)-\varepsilon(t-2)]
\end{align}
\]
时域微分性质
\[若f(t)\leftrightarrow F(j\omega)\quad 则: \frac{d}{dt} f(t)\leftrightarrow j\omega F(j\omega)
\]
\[\frac{d^{n}}{dt^{n}}f(t)\leftrightarrow(j\omega)^{n}F(j\omega)
\]
推导:
\[\begin{align}
&已知 \frac{d}{dt}f(t)=f(t)*\delta'(t)\\ \\
&而f(t)\leftrightarrow F(t)\quad \delta'(t)\leftrightarrow j\omega\\ \\
&则 \frac{d}{dt}f(t)= f(t)*\delta'(t)\leftrightarrow j\omega F(t)
\end{align}
\]
- 利用了\(\delta'(t)\)卷积的求导性质
- 利用了时域卷积性质\(f_{1}(t)*f_{2}(t)\leftrightarrow F_{1}(t)\cdot F_{2}(t)\)
例
求解信号\(f(t)=\frac{1}{t^{2}}\)的傅里叶变换
\[\begin{align}
&已知sgn(t)\leftrightarrow \frac{2}{j\omega}\\ \\
&\implies \frac{2}{jt}\leftrightarrow 2\pi sgn(-\omega)=-2\pi sgn(\omega)\\ \\
&\implies \frac{1}{t}\leftrightarrow -j\pi sgn\omega\\ \\
& 则 \frac{d}{dt}\left( \frac{1}{t} \right)=-\frac{1}{t^{2}}\leftrightarrow(j\omega)(-j\pi sgn(\omega))=\pi \omega sgn(\omega)\\ \\
&\therefore \frac{1}{t^{2}}\leftrightarrow-\pi \omega sgn(\omega)=-\pi |\omega|
\end{align}
\]
- 关键点:由\(\frac{1}{t}\)的反比例结构联想到\(sgn(t)\)的傅里叶变换\(\frac{2}{j\omega}\)
时域积分性质
\[\begin{align}
&若f(t)\leftrightarrow F(j\omega)\\ \\
&则 \int_{{-\infty}}^{t}f(\tau)d\tau \leftrightarrow \frac{1}{j\omega}F(j\omega)+\pi F(0)\delta(\omega)\\ \\
&且\ F(0)=F(j\omega)\bigg|_{\omega=0}=\int_{-\infty}^{+\infty}f(t)dt
\end{align}
\]
推导:
\[\begin{align}
&已知\int_{-\infty}^{t}f(\tau)d\tau=f(t)*\varepsilon(t)\\ \\
&而f(t)\leftrightarrow F(j\omega)\quad \varepsilon(t)\leftrightarrow \pi \delta(\omega)+ \frac{1}{j\omega}\\ \\
&\therefore f(t)*\varepsilon(t)\leftrightarrow F(j\omega)\cdot\left[ \omega \delta(\omega)+ \frac{1}{j\omega} \right]=\pi F(0)\delta(\omega)+ \frac{F(j\omega)}{j\omega}
\end{align}
\]
- 利用了\(\varepsilon(t)\)卷积的积分性质
- 利用了时域卷积性质\(f_{1}(t)*f_{2}(t)\leftrightarrow F_{1}(t)\cdot F_{2}(t)\)
时域积分性质的使用注意事项
\[求导\to傅里叶变换\to 时域积分
\]
\[\begin{align}
&若f_{1}(t)=f'(t)\leftrightarrow F_{1}(j\omega)\\ \\
&则f(t)\leftrightarrow \frac{F_{1}(j\omega)}{j\omega}+\pi[f(-\infty)+f(+\infty)]\delta(\omega)
\end{align}
\]
推导:
\[\begin{align}
&\int_{-\infty}^{t}f_{1}(x)dx=\int_{-\infty}^{t} \frac{df(x)}{dx}dx=f(t)-f(-\infty)\leftrightarrow \frac{F_{1}(j\omega)}{j\omega}+\pi F_{1}(0)\delta(\omega)\\ \\
&而f(t)\leftrightarrow F(j\omega)\quad f(-\infty)\leftrightarrow 2\pi f(-\infty)\delta(\omega)\\ \\
&则f(t)-f(-\infty)\leftrightarrow F(j\omega)-2\pi f(-\infty)\delta(\omega)= \frac{F_{1}(j\omega)}{j\omega}+\pi F_{1}(0)\delta(\omega)\\ \\
&将F_{1}(0)=\int_{-\infty}^{+\infty}f_{1}(x)dx=\int_{-\infty}^{+\infty} \frac{df(x)}{dx}dx=f(+\infty)-f(-\infty)代入上式:\\ \\
&\implies f(t)\leftrightarrow F(j\omega)= \frac{F_{1}(j\omega)}{j\omega}+\pi[f(-\infty)+f(+\infty)]\delta(\omega)
\end{align}
\]
- 公式发生改变的根本原因:求导后积分不一定得到原函数!
- 特别地,若\(f(-\infty)+f(+\infty)=0\),设\(f^{(n)}(t)\leftrightarrow F_{n}(j\omega)\),则:
\[f(t)\leftrightarrow \frac{F_{n}(j\omega)}{(j\omega)^{n}}
\]
- 因此当傅里叶变换难求时,可尝试求其微分后的傅里叶变换
例
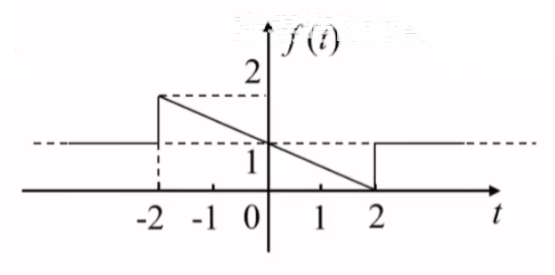
求图示信号的傅里叶变换
\[\begin{align}
&由图示可知f'(t)=- \frac{1}{2} g_{4}(t)+\delta(t-2)+\delta(t+2)\\ \\
&已知\cos \omega_{0}t \leftrightarrow \pi[\delta(\omega-\omega_{0})+\delta(\omega+\omega_{0})] \\ \\
& \implies \delta(t+\omega_{0})+\delta(t-\omega_{0})\leftrightarrow 2\cos 2\omega_{0}\omega \\ \\
&则f'(t)\leftrightarrow -2Sa(2\omega)+2\cos 2\omega=F_{1}(j\omega)\\ \\
&而f(t)\leftrightarrow F(j\omega)= \frac{F_{1}(j\omega)}{j\omega}+\pi[f(-\infty)+f(+\infty)]\delta(\omega),f(+\infty)+f(-\infty)=2 \\ \\
&则f(t)\leftrightarrow \frac{2\cos 2\omega-2Sa(2\omega)}{j\omega}+2\pi \delta(\omega)
\end{align}
\]
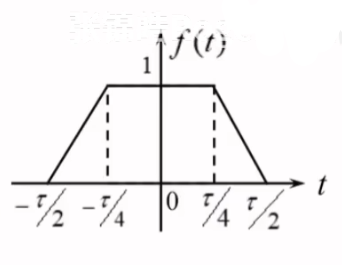
求解图示信号的傅里叶变换。
\[\begin{align}
&由图示可知,f''(t)=\frac{4}{\tau}\left[ \delta\left( t+\frac{\tau}{2} \right) -\delta\left( t+\frac{\tau}{4} \right)-\delta\left( t-\frac{\tau}{4} \right)+\delta\left( t+\frac{\tau}{2} \right)\right]\\ \\
&f''(t)\leftrightarrow \frac{4}{\tau}\left[ e^{\frac{1}{2}j\tau \omega}-e^{ \frac{1}{4}j\tau \omega }-e^{- \frac{1}{4}j\tau \omega}+e^{- \frac{1}{2}j\tau \omega} \right]=\frac{8}{\tau}\left[ \cos \frac{1}{2}\tau \omega -\cos \frac{1}{4}\tau \omega\right]\\ \\
&而f(+\infty)+f(-\infty)=0\\ \\
&\therefore f(t)\leftrightarrow \frac{F_{n}(j\omega)}{(j\omega)^{n}}=- \frac{8}{\omega^{2}\tau}\left[ \cos \frac{\tau}{2}\omega-\cos \frac{\tau}{4}\omega \right]
\end{align}
\]
计算积分\(\int_{-\infty}^{+\infty}Sa(t)\cos(2t)dt\)
\[\begin{align}
&已知F(0)=\int_{-\infty}^{+\infty}f(t)dt=F(j\omega)\bigg|_{\omega=0}\\ \\
&而Sa(t)\leftrightarrow \pi g_{2}(\omega)\\ \\
&\cos 2t\leftrightarrow \pi[\delta(\omega+2)+\delta(\omega-2)]\\ \\
&\implies Sa(t)\cos 2t\leftrightarrow \frac{1}{2\pi}\cdot \pi g_{2}(\omega)*\pi[\delta(\omega+2)+\delta(\omega-2)]\\ \\
&\implies F(j\omega)=\frac{\pi}{2}[g_{2}(\omega+2)+g_{2}(\omega-2)]\\ \\
&则\int_{-\infty}^{+\infty}Sa(t)\cos 2tdt=\int_{-\infty}^{+\infty}f(t)dt=F(j\omega)\bigg|_{\omega=0}=0\\ \\
&\therefore \int_{-\infty}^{+\infty}Sa(t)\cos 2tdt=0
\end{align}
\]
- 当积分难以计算时,可以尝试使用傅里叶变换的时域积分性质进行求解
3.4 傅里叶变换的性质 III
频域微分性质
\[\begin{align}
&f(t)\leftrightarrow F(j\omega),则:\\ \\
&(-jt)f(t)\leftrightarrow \frac{d}{dt}F(j\omega)\quad (-jt)^{n}f(t)\leftrightarrow \frac{d^{n}}{d\omega^{n}}F(j\omega)\\
\end{align}
\]
推导:
\[\begin{align}
& \frac{d}{d\omega}F(j\omega)=F(j\omega)*\delta'(\omega)\\ \\
&而\delta'(t)\leftrightarrow j\omega\implies - \frac{jt}{2\pi}\leftrightarrow \delta'(\omega)\\ \\
&且f(t)\leftrightarrow F(j\omega)\\ \\
&则F(j\omega)*\delta'(\omega)\leftrightarrow 2\pi \cdot f(t)\cdot \left( - \frac{jt}{2\pi} \right)=-jt\cdot f(t)\\ \\
&\therefore (-jt)f(t)\leftrightarrow \frac{d}{d\omega}F(j\omega) \quad 或 \quad tf(t)\leftrightarrow j \frac{d}{d\omega}F(j\omega)
\end{align}
\]
- 频域微分性质与时域微分性质对称:
- \(\frac{d}{dt}f(t)\leftrightarrow j\omega F(j\omega)\)
- \(tf(t)\leftrightarrow jF'(j\omega)\)
频域积分性质
\[\begin{align}
&f(t)\leftrightarrow F(j\omega)\\ \\
&则\pi f(0)\delta(t)+ \frac{1}{-jt}f(t)\leftrightarrow F^{(-1)}(j\omega)=\int_{-\infty}^{\omega}F(jx)dx\\ \\
&f(0)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}d\omega=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)d\omega
\end{align}
\]
推导:
\[\begin{align}
&\int_{-\infty}^{\omega}F(jx)dx=F(j\omega)*\varepsilon(\omega)\\ \\
&而\varepsilon(t)\leftrightarrow \pi \delta(\omega)+ \frac{1}{j\omega}\\ \\
&\implies \pi \delta(t)+ \frac{1}{jt}\leftrightarrow 2\pi \varepsilon(-\omega)=2\pi[1-\varepsilon(\omega)]\\ \\
&\implies \frac{1}{2}\delta(t)- \frac{1}{jt}\cdot \frac{1}{2\pi}\leftrightarrow \varepsilon(\omega)\\ \\
&而f(t)\leftrightarrow F(j\omega)\\ \\
&则 2\pi \cdot f(t)\cdot \left[ \frac{1}{2}\delta(t)- \frac{1}{jt}\cdot \frac{1}{2\pi} \right] \leftrightarrow F(j\omega)*\varepsilon(\omega)\\ \\
&\implies \pi f(0)\delta(t)+ \frac{1}{-jt}f(t)\leftrightarrow \int_{-\infty}^{\omega}F(jx)dx
\end{align}
\]
- 频域积分性质与时域积分性质对称:
- \(\int_{-\infty}^{t}f(\tau)d\tau \leftrightarrow \pi F(0)\delta(\omega)+ \frac{F(j\omega)}{j\omega}\)
- \(\pi f(0)\delta(t)+ \frac{1}{-jt}f(t)\leftrightarrow F^{(-1)}(j\omega)\)
例
计算\(\int_{{-\infty}}^{+\infty} \frac{\sin 2\omega}{\omega}d\omega\)
\[\begin{align}
&f(0)= \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)d\omega\\ \\
&令F(j\omega)= \frac{2\sin 2\omega}{2\omega}=2Sa(2\omega)\quad 而 \frac{1}{2}g_{4}(t)\leftrightarrow 2Sa(2\omega)\\ \\
&\implies f(t)= \frac{1}{2}g_{4}(t)\leftrightarrow F(j\omega)\\ \\
&\implies \int_{-\infty}^{+\infty} \frac{\sin 2\omega}{\omega}d\omega=2\pi f(0)=\pi
\end{align}
\]
求负无穷到正无穷上的积分:
\[\begin{align}
&\int_{-\infty}^{+\infty}f(t)dt=F(0)\\ \\
&\int_{-\infty}^{+\infty}F(j\omega)d\omega
=2\pi f(0)\end{align}
\]
能量定理
非周期信号与频谱函数的关系:
\[Parseval定理:E=\int_{-\infty}^{+\infty}|f(t)|^{2}dt= \frac{1}{2\pi}\int_{-\infty }^{+\infty}|F(j\omega)|^{2}d\omega
\]
能量谱密度函数:
\[\varepsilon(\omega)=|F(j\omega)|^{2}
\]
例
求信号\(f(t)= \frac{2}{t^{2}+1}\)的能量
\[\begin{align}
&已知 e^{-\alpha |t|}\leftrightarrow \frac{2\alpha}{\alpha^{2}+\omega^{2}}\implies e^{-|t|}\leftrightarrow \frac{2}{\omega^{2}+1}\\ \\
&\implies \frac{2}{t^{2}+1}\leftrightarrow 2\pi e^{-|\omega|}\\ \\
&E=\frac{1}{2\pi_{}}\int_{-\infty}^{+\infty}|F(j\omega)|^{2}d\omega=\frac{1}{2\pi}\int_{-\infty}^{+\infty}4\pi^{2}e^{-2|\omega|}d\omega\\ \\
&=2\pi \cdot 2\int_{0}^{+\infty}e^{-2\omega}d\omega=2\pi\ (J)
\end{align}
\]
例
![[Pasted image 20250917192811.png]]
图示信号频谱函数为\(F(j\omega)\),不计算\(F(j\omega)\),求:
- 1)\(F(j\omega)\)的相位函数\(\varphi(\omega)\)
\[\begin{align}
&1):\\ \\
&令f_{1}(t)=f(t+1)\quad f(t)为实、偶函数\quad 设f_{1}(t)\leftrightarrow F_{1}(j\omega)\\ \\
&则F_{1}(j\omega)为实、偶函数\quad F_{1}(j\omega)=|F_{1}(j\omega)|\cdot e^{\varphi_{1}(\omega)}\\ \\
&\implies \varphi_{1}(\omega)=\begin{cases}
0\quad F_{1}(j\omega)>0\\ \\
\pi\quad F_{1}(j\omega)<0
\end{cases}\\ \\
&f(t)=f_{1}(t-1)\quad F(j\omega)=F_{1}(j\omega)\cdot e^{-j\omega}\\ \\
&\therefore \varphi(\omega)=\varphi_{1}(\omega)-\omega=\begin{cases}
-\omega\quad F_{1}(j\omega)>0\\ \\
\pi-\omega\quad F_{1}(j\omega)<0
\end{cases}
\end{align}
\]
\[\begin{align}
&E=\int_{-\infty}^{+\infty}f^{2}(t)dt= \frac{1}{2\pi}\int_{-\infty}^{+\infty}|F(j\omega)|d\omega\\ \\
&\therefore \int_{-\infty}^{+\infty}|F(j\omega)|^{2}d\omega=2\pi \int_{-\infty}^{+\infty}f^{2}(t)dt=\int_{-1}^{0}4dt+\int_{0}^{1}(2-t)^{2}dt+\int_{1}^{2}t^{2}dt+\int_{2}^{3}4dt\\ \\
&=\frac{76}{3}\pi
\end{align}
\]
- 3)求\(\int_{-{\infty}}^{+\infty}F(j\omega) \frac{2\sin \omega}{\omega}e^{j 2\omega}d\omega\)
\[\begin{align}
&令X(j\omega)=F(j\omega)\cdot \frac{2\sin \omega}{\omega}=F(j\omega)\cdot 2Sa(\omega)\\ \\
&则X(j\omega)\leftrightarrow f(t)*g_{2}(t)=x(t)\\ \\
&而x(t)=f(t)*g_{2}(t)= \frac{1}{2\pi}\int_{-\infty}^{+\infty}X(j\omega)e^{j\omega t}d\omega\\ \\
&\implies x(2)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(j\omega)^{j 2t}d\omega\\ \\
&x(2)=f(t)*g_{2}(t)\bigg|_{t=2}=\int_{-\infty}^{+\infty}f(\tau)g_{2}(2-\tau)d\tau\\ \\
&画图可知x(2)=\int_{1}^{2}\tau d\tau+\int_{2}^{3}2d\tau=\frac{7}{2}\\ \\
&\therefore \int_{-\infty}^{+\infty}F(j\omega)\cdot \frac{2\sin \omega}{\omega}e^{j 2\omega}d\omega=2\pi x(2)=7\pi
\end{align}
\]
\[\begin{align}
&\mathrm{Re}[F(j\omega)]\leftrightarrow f_{ev}(t)= \frac{f(t)+f(-t)}{2}\\ \\
&\therefore 画出f_{ev}(t)波形即可
\end{align}
\]
\[\begin{align}
&f_{ev}(t)= \frac{f(t)+f(-t)}{2}\leftrightarrow \mathrm{Re}[F(j\omega)]=R(\omega)\\ \\
&f_{od}(t)= \frac{f(t)-f(-t)}{2}\leftrightarrow j\cdot \mathrm{Im}[F(j\omega)]=j\cdot X(\omega)
\end{align}
\]
3.4* 信号的能量谱与功率谱
能量信号的相关定理与能量谱
对于能量信号,互相关函数定义为:
\[\begin{align}
&R_{12}(\tau)=\int_{-\infty}^{+\infty}f_{1}(t)f_{2}(t-\tau)dt=\int_{-\infty}^{+\infty}f_{1}(t+\tau)f_{2}(t)dt\\ \\
&R_{21}(\tau)=\int_{-\infty}^{+\infty}f_{1}(t-\tau)f_{2}(t)dt=\int_{-\infty}^{+\infty}f_{1}(t)f_{2}(t+\tau)dt
\end{align}
\]
- 注意:角标数字中,前面的信号领先时间\(\tau\)
互相关函数的傅里叶变换满足:
\[\begin{align}
&若f_{1}(t)\leftrightarrow F_{1}(j\omega)\quad f_{2}(t)\leftrightarrow F_{2}(j\omega)\\ \\
&则\begin{cases}
R_{12}(\tau)\leftrightarrow F_{1}(j\omega)\cdot F^{*}_{2}(j\omega)\\ \\
R_{21}(\tau)\leftrightarrow F_{1}^{*}(j\omega)\cdot F_{2}(j\omega)
\end{cases}
\end{align}
\]
- 其中,\(F^{*}(j\omega)\)代表复数函数\(F(j\omega)\)的共轭函数
对于自相关函数:
\[\begin{align}
&R(\tau)=\int_{-\infty}^{+\infty}f(t)f(t-\tau)dt
\end{align}
\]
\[\begin{align}
&R(\tau)\leftrightarrow F(j\omega)\cdot F^{*}(j\omega)=|F(j\omega)|^{2}\\ \\
&令\tau=0\quad R(0)=\int_{-\infty}^{+\infty}f^{2}(t)dt=E
\end{align}
\]
- 自相关函数的傅里叶变换为信号的能量谱函数
- 自相关函数的0处值为能量信号的能量
功率信号的功率谱与维纳-辛钦定理
从信号\(f(t)\)猴子那个截取\(|t|\leq T/2\)的一段,得到一个\(T\)长截断函数\(f_{T}(t)\):
\[f_{T}(t)=f(t)\left[ e\left( t+\frac{T}{2} \right)-\varepsilon\left( t-\frac{T}{2} \right) \right]
\]
则\(T\)有限时,函数\(f_{T}(t)\)为能量信号,其能量为:
\[\begin{align}
&E_{T}=\int_{-\infty}^{+\infty}f^{2}_{T}(t)dt=\int_{-\frac{T}{2}}^{\frac{T}{2}}f^{2}(t)dt=\frac{1}{2\pi}\int_{-{\infty}}^{+\infty}|F_{T}(j\omega)|^{2}d\omega\quad \mathcal{F}[f_{T}(t)]=F_{T}(j\omega)\\ \\
&P=\lim_{ T \to \infty } \frac{1}{T}\int_{_{\frac{T}{2}}}^{\frac{T}{2}}f^{2}(t)dt=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\lim_{ T \to \infty }
\frac{|F_{T}(j\omega)|^{2}}{T}d\omega
\end{align}
\]
功率密度谱:
\[P(\omega)=\lim_{ T \to \infty } \frac{|F_{T}(j\omega)|^{2}}{T}
\]
- 功率谱为\(\omega\)的偶函数,仅取决于频谱函数的模量
功率信号自相关函数:
\[R(\tau)=\lim_{ T \to \infty } \left[ \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)f(t-\tau)dt \right]
\]
\[\begin{align}
\mathcal{F}[R(\tau)]&=\mathcal{F}\left[ \lim_{ T \to \infty } \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)f(t-\tau)dt \right]\\ \\
&=\lim_{ T \to \infty } \frac{1}{T}\mathcal{F}\left[ \int_{-\infty}^{+\infty}f_{T}(t)f_{T}(t-\tau)dt \right]\\ \\
&=\lim_{ T \to \infty } \frac{|F_{T}(j\omega)|^{2}}{T}\\ \\
&\implies R(\tau)\leftrightarrow P(\omega)
\end{align}
\]
- 结论:功率信号的功率谱与自相关函数是一对傅里叶变换,称为维纳-辛钦定理
总结:
\[\begin{align}
&能量信号:R(\tau)\leftrightarrow |F(j\omega)|^{2}\\ \\
&功率信号\quad R(t)\leftrightarrow \lim_{ T \to \infty } \frac{|F_{T}(j\omega)|^{2}}{T} =P(\omega)
\end{align}
\]
3.5 周期信号的傅里叶变换
一般周期信号的傅里叶变换
周期为\(T\)的周期信号可以展开为指数形式的傅里叶级数:
\[\begin{align}
&f_{T}(t)=\sum_{n=-\infty}^{+\infty}F_{n}e^{jn\Omega t},\Omega=\frac{2\pi}{T}\\ \\
&\mathcal{F}[f_{T}(t)]=\mathcal{F}\left[ \sum_{n=-\infty}^{+\infty}F_{n}e^{jn\Omega t} \right]
\end{align}
\]
而\(F_{n}\)与\(t\)无关,因此:
\[\begin{align}
&\mathcal{F}[f_{T}(t)]=\sum_{n=-\infty}^{+\infty}F_{n}\mathcal{F}[e^{jn\Omega t}]\\ \\
&而1\leftrightarrow 2\pi \delta(\omega)\\ \\
&\implies e^{jn\Omega}\leftrightarrow 2\pi \delta(\omega-n\Omega)
\end{align}
\]
一般周期信号的傅里叶变换:
\[\begin{align}
&\mathcal{F}[f_{t}(t)]=2\pi \sum_{nm=-\infty }^{+\infty}F_{n}\delta(\omega-n\Omega),\Omega= \frac{2\pi}{T}
\end{align}
\]
- 周期信号的频谱密度由冲激序列组成
- 冲激位置:\(\omega=n\Omega\),谐波频率处
- 冲激强度:\(2\pi F_{n}\)由傅里叶系数确定
例
求周期冲激序列\(\delta_{T}(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT)\)的傅里叶变换
\[\begin{align}
&F_{n}= \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\delta_{T}(t)e^{-jn\Omega t}dt=\frac{1}{T}[e^{-jn\Omega t}]\bigg|_{t=0}=\frac{1}{T}\\ \\
&而f_{T}(t)\leftrightarrow 2\pi \sum_{n=-\infty}^{+\infty}\delta(t-nT) \\ \\
&\delta_{T}(t)\leftrightarrow 2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega)= \frac{2\pi}{T}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega)=\Omega \delta_{\Omega}(\omega)
\end{align}
\]
结论:
\[\delta_{T}(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT) \leftrightarrow \Omega \sum_{n=-\infty }^{+\infty}\delta(\omega-n\Omega)=\Omega \delta_{\Omega}(\omega),\Omega=\frac{2\pi}{T}
\]
周期信号傅里叶系数与傅里叶变化的关系
任意周期为\(T\)的周期信号\(f_{T}(t)\)可以表示为第一个周期内的脉冲信号\(f_{0}(t)\)和周期冲激序列卷积的结果
\[\begin{align}
&f_{t}(t)=f_{0}(t)*\delta_{T}(t)=f_{0}(t)*\sum_{n=-\infty}^{+\infty}\delta(t-nT)\\ \\
&F(j\omega)=F_{0}(j\omega)\cdot \Omega \sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega)=\Omega \sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega)\\ \\
&=\Omega \sum_{n=-\infty}^{+\infty}F_{0}(jm\Omega)\delta(\omega-n\Omega)\\ \\
&而F(j\omega)=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega)\\ \\
&\implies 2\pi F_{n}=\Omega F_{0}(jn\Omega)\implies F_{n}=\frac{1}{T}F_{0}(jn\Omega)=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}
\end{align}
\]
求解周期信号傅里叶变换的方法
\[\begin{align}
&\mathcal{F}[f_{T}(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega),\Omega=\frac{2\pi}{T}\\ \\
&F_{n}=\frac{1}{T}F_{0}(jn\Omega)=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}
\end{align}
\]
- 找周期信号在第一个周期内的单体\(f_{0}(t)\)
- 求\(f_{0}(t)\)对应的傅里叶变换\(F_{0}(j\omega)\)
- 周期信号的傅里叶系数为\(F_{n}=\frac{1}{T}F_{0}(jn\Omega)=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}\)
- 周期信号的傅里叶变换\(\mathcal{F}[f_{T}(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega),\Omega=\frac{2\pi}{T}\)
例
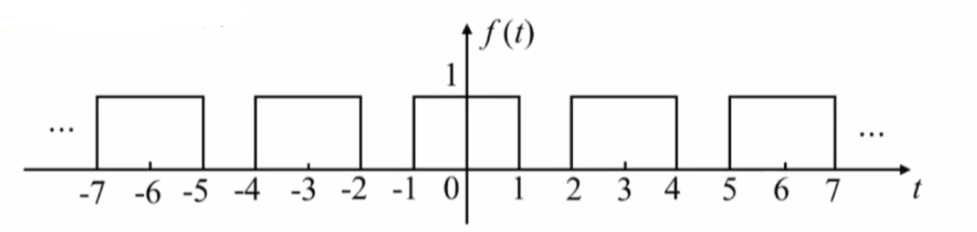
已知周期举行脉冲信号如图所示,求此信号的傅里叶变换与指数形式的傅里叶级数
\[\begin{align}
&f_{0}(t)=g_{2}(t),\ T=3,\ \Omega=\frac{2\pi}{T}= \frac{2\pi}{3}\\ \\
&f_{0}(t)\leftrightarrow 2Sa(\omega)=F_{0}(j\omega)\\ \\
&F_{n}=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}=\frac{2}{3}Sa\left( \frac{2\pi}{3}n \right)\\ \\
&\therefore \mathcal{F}[f_{T}(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega- n\Omega)\\ \\
&=\frac{4\pi}{3}\sum_{n=-\infty}^{{+\infty}}Sa\left( \frac{2\pi}{3}n \right)\cdot \delta\left( \omega-\frac{2\pi}{3}n \right)\\ \\
&\therefore f(t)=\sum_{n=-\infty}^{+\infty}F_{n}e^{jn\Omega t}=\frac{2}{3}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{2\pi}{3}n \right)e^{j \frac{2\pi}{3}nt}
\end{align}
\]
- 注意\(f_{0}(t)\)的定义域不一定要从原点开始取
- 将周期函数展开为傅里叶级数多了一种新思路:求基波信号的傅里叶变换,再求原函数的傅里叶级数系数,从而得到傅里叶级数
3.6 抽样定理
理想抽样及其信号的频谱
抽样的概念

抽样可以将模拟信号转化为一系列事件离散的样值信号。实际中多采用均匀抽样,抽样间隔\(T_{s}\)即为抽样周期,\(f_{s}=\frac{1}{T}\)称为抽样频率
\[f_{s}(t)=f(t)\cdot s(t)
\]
理想抽样信号及其频谱
\[\begin{align}
冲激脉冲序列:s(t)&=\delta_{T_{s}}(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})\\ \\
理想抽样信号:f_{s}(t)&=f(t)\cdot \delta_{T}(t)=f(t)\cdot \sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})\\ \\
&=\sum_{n=-\infty}
^{+\infty}f(nT_{s})\delta(t-nT_{s})\end{align}
\]
\[\begin{align}
s(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})\leftrightarrow S(j\omega)&=\Omega_{s}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega_{s}),\Omega_{s}=\frac{2\pi}{T_{s}}\\ \\
f_{s}(t)=f(t)\cdot s(t)\leftrightarrow F_{s}(j\omega)&=\frac{1}{2\pi}F(j\omega)*S(j\omega)\\ \\
&=\frac{1}{2\pi}F(j\omega)*\Omega_{s}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega_{s})\\ \\
&=\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}F[j(\omega-n\Omega_{s})]
\end{align}
\]
结论:
\[F_{s}(j\omega)=\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}F[j(\omega-n\Omega_{s})]
\]
- \(F_{s}(j\omega)\)为信号频谱\(F(j\omega)\)以\(\Omega_{s}\)为周期延拓
- 频谱幅度变为原先的\(\frac{1}{T}\)
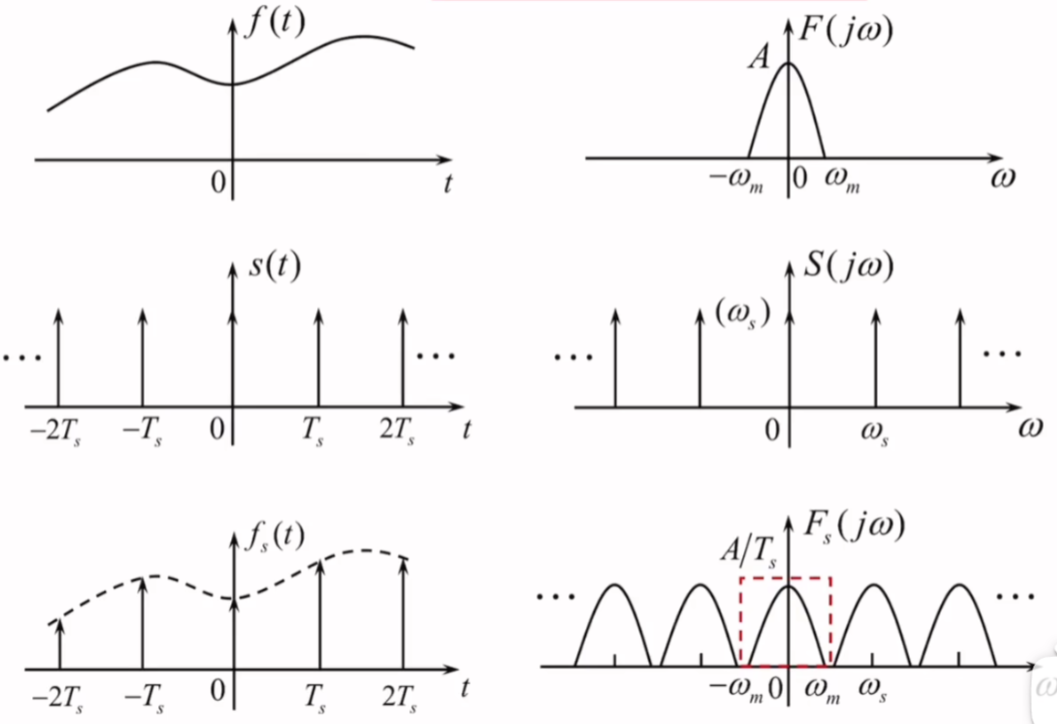
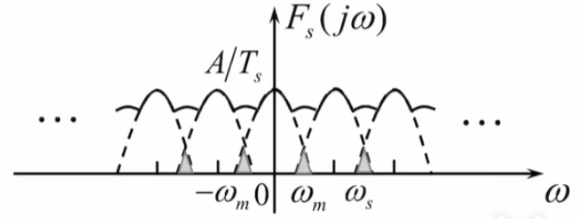
理想抽样信号及其频谱示意图:
-
\(f_{s}\geq 2f_{m}\)时,各个频谱之间无混叠,可以分离出原信号的频谱
- 由抽样序列\(\{ f(nT_{s}) \}\)可以无失真地恢复出\(f(t)\)
-
\(f_{s}<2f_{m}\)时,频谱之间产生混叠,无法分离出原信号的频谱
- 由\(\{ f(nT_{s}) \}\)不能无失真地恢复\(f(t)\)
-
其中\(\omega_{m}\)为原式连续信号的最高角频率,代表频谱的有效带宽
例


- 当\(f_{s}<2f_{m}\)时,频谱图像会存在重叠
矩形抽样及其信号的频谱
矩形抽样的定义:
抽样脉冲为矩形脉冲,此时抽样信号的脉冲顶部随着原信号\(f(t)\)变化,这样的抽样称为矩形抽样
矩形抽样的频谱:
设矩形脉冲脉宽为\(\tau\),周期为\(T\)
\[\begin{align}
s(t)&=g_{\tau}(t)*\delta_{T}(t)\\ \\
S(j\omega)&=\tau Sa\left( \frac{\omega \tau}{2} \right)\cdot \frac{2\pi}{T}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\omega_{s})=\frac{2\pi \tau}{T_{s}}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{n\omega_{s}\tau}{2} \right)\delta(\omega-n\omega_{s})\\ \\
而f_{s}(t)&=f(t)\cdot s(t)\\ \\
则F_{s}(j\omega)&=\frac{1}{2\pi}F(j\omega)*S(j\omega)=\frac{\tau}{T}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{n\omega_{s}\tau}{2} \right)F[j(\omega-n\omega_{s})]
\end{align}
\]
结论:
\[F_{s}(j\omega)=\frac{\tau}{T_{s}}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{n\omega_{s}\tau}{2} \right)F[j(\omega-n\omega_{s})]
\]
- \(F_{s}(j\omega)\)为\(Sa\)函数加权,包络满足\(Sa\)函数的变化规律
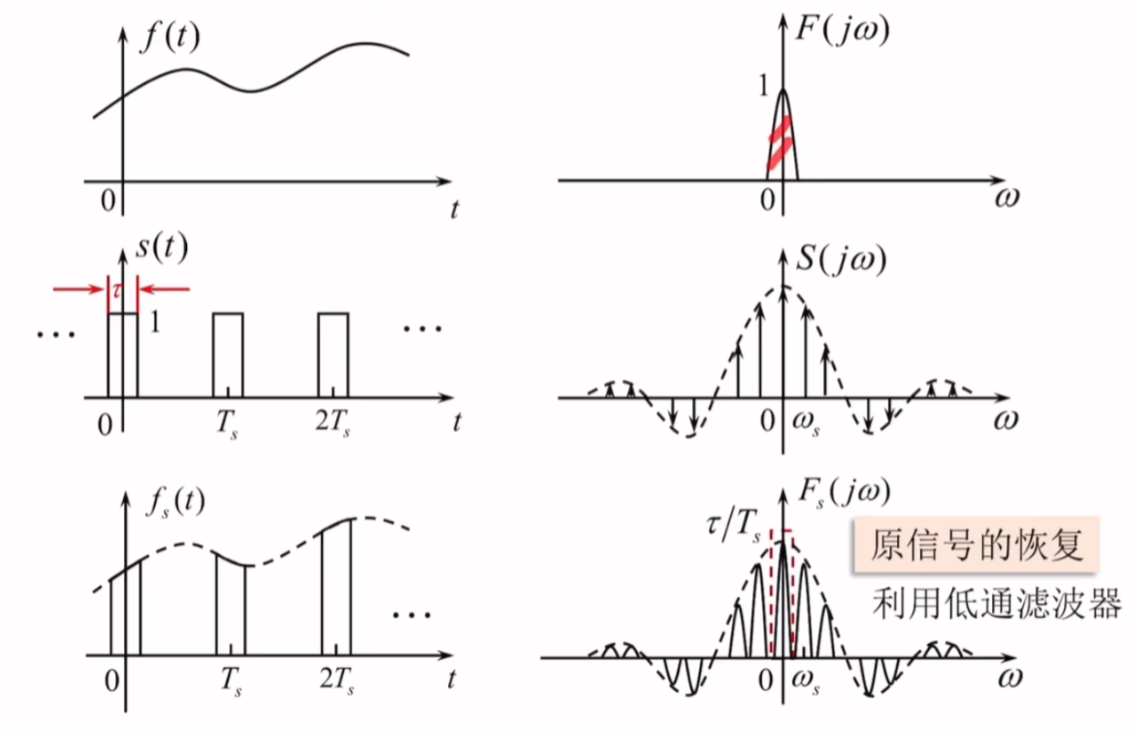
- 当\(f_{s}\geq2 f_{m}\)时,同样可以通过低通滤波器来还原出原信号
理想抽样与矩形抽样的异同点
相同点:
- 均为无穷多个间隔为\(\omega_{s}\)的\(F(j\omega)\)叠加而成的
- 抽样频率满足要求时,均可以通过低通滤波器恢复原信号
不同点:
- 矩形理想抽样信号频谱被常数加权,带宽无穷大
- 矩形抽样信号频谱被\(Sa\)函数加权,最终收敛于0,第一过零点带宽为\(B_{\omega}=\frac{2\pi}{\tau}(rad/s)\)或\(B_{f}=\frac{1}{\tau}(Hz)\)
\[提高传输速度\xLeftrightarrow{矛盾}压缩传输带宽
\]
时域抽样定理
- \(f_{s}\geq{2}f_{m}\)时,各个频谱之间没有混叠,可以分离出原信号的频谱
- \(f_{s}<2f_{m}\)时,频谱之间产生混叠,无法分离出原信号的频谱
定理:
一个频带限制在\((0,f_{m})\)内的低通信号\(f(t)\),如果以\(f_{s}\geq2 f_{m}\)的速率进行均匀抽样,则由抽样序列\(\{ f(nT_{s}) \}\)可以无失真恢复出\(f(t)\)
\[\begin{align}
&奈奎斯特抽样速率:f_{s}=2f_{m}\implies最小抽样速率\\ \\
&奈奎斯特抽样间隔:T_{s}=\frac{1}{2f_{m}}\implies最大抽样间隔
\end{align}
\]
在工程中,若信号不是频带有限信号,则往往通过截止频率\(f_{m}\)的低通滤波器让其频带有限,称为抗混叠滤波
例
若信号\(f_{1}(t)\)和\(f_{2}(t)\)的最高角频率分别为\(3\pi \times 10^{5}rad/s\)和\(2\pi \times 10^5rad/s\),试求下列信号进行时域抽样时的奈奎斯特抽样频率
1)\(f_{1}\left( \frac{1}{2}t \right)\)
\[\begin{align}
&f_{1}=\frac{\omega_{1m}}{2\pi}=1.5\times 10^{5}Hz,f_{2}=\frac{\omega_{2m}}{2\pi}=10^{5}Hz\\ \\
&f_{1}\left( \frac{1}{2}t \right)\leftrightarrow 2F_{1}(j\cdot 2\omega)\xrightarrow{拉伸} f_{m}=\frac{1}{2}f_{1}=7.5\times 10^{4}Hz\\ \\
&\implies f_{s}=2f_{m}=1.5\times 10^{5}Hz
\end{align}
\]
- 角频率有两种单位\(rad,Hz\),其中\(rad\)单位除以\(2\pi\)后可以转换成\(Hz\)
2)\(f_{2}^{3}(t)\)
\[\begin{align}
&f_{2}^{3}(t)\leftrightarrow \frac{1}{(2\pi)^{2}}[F_{2}(j\omega)*F_{2}(j\omega)*F_{2}(j\omega)]\\ \\
&\implies f_{m}=3f_{2}=3\times 10^{5}Hz\\ \\
&\implies f_{s}=2f_{m}=6\times 10^{5}Hz
\end{align}
\]
- 利用卷积积分的定义域叠加性质:
- 若\(f(t)\)定义域为\([t_{1},t_{2}]\),\(g(t)\)的定义域为\([t_{3},t_{4}]\)
- 则\(f(t)*g(t)\)定义域为\([t_{1}+t_{3},t_{2}+t_{4}]\)
- 三次自卷积后,最高角频率扩大三倍
3)\(f_{1}(t)\cdot f_{2}(t)\)
\[\begin{align}
&f_{1}(t)\cdot f_{2}(t)\leftrightarrow \frac{1}{2\pi}F_{1}(j\omega)*F_{2}(j\omega)\\ \\
&f_{m}=f_{1}+f_{2}=2.5\times 10^{5}Hz\\ \\
&\implies f_{s}=2f_{m}=5\times 10^{5}Hz
\end{align}
\]
4)\(f_{1}(t)*f_{2}(2t)\)
\[\begin{align}
&f_{1}(t)*f_{2}(2t)\leftrightarrow F_{1}(j\omega)\cdot \frac{1}{2}F_{2}\left( \frac{1}{2}j\omega \right)\\ \\
&f_{m}=min\{ f_{1},2f_{2} \}=f_{1}=3\times 10^{5}Hz
\end{align}
\]
- 两个信号做乘法,新信号的最高角频率为两个原信号最高角频率中的最小值
5)\(f_{1}(t)+f_{2}(2t)\)
\[\begin{align}
&f_{1}(t)+f_{2}(2t)\leftrightarrow F_{1}(j\omega)+\frac{1}{2}F_{2}\left( \frac{1}{2}j\omega \right)\\ \\
&\implies f_{m}=max\{ f_{1},2f_{2} \}=2\times 10^{5}Hz
\end{align}
\]
- 两个信号做加法,新信号的最高角频率为两个原信号的最高角频率中的最大值

- 注意\(F\left( j\cdot \frac{\omega}{\alpha} \right)\)所对应的最高角频率为\(|\alpha|\omega\)
时域原信号的恢复
利用低通滤波器来恢复原信号
\[\begin{align}
H(j\omega)&=\begin{cases}
T_{s},\quad |\omega|\leq \omega_{c}\\ \\
0,\quad |\omega|>\omega_{c}
\end{cases}\\ \\
&=T_{s}\cdot g_{2\omega _{c}}(\omega)
\end{align}
\]
截止频率需要满足:
\[\omega_{m}\leq \omega_{c}\le \omega_{s}-\omega_{m}
\]
例
带限信号\(f(t)\)的最高频率为\(300Hz\),若对\(y(t)=\frac{1}{2}\left[ f\left( \frac{t}{3} \right)*f(2t) \right]\cdot f(t)\)以\(T_{s}=1ms\)进行抽样,低通滤波器的截止频率\(f_{c}\)应该满足什么范围?
\[\begin{align}
&若f(t)\sim f_{m}\\ \\
&则f\left( \frac{t}{3} \right)\sim \frac{f_{m}}{3}\ ,\ f(2t)\sim 2f_{m}\\ \\
&f\left( \frac{t}{3} \right)*f(2t)\leftrightarrow F\left( \frac{t}{3} \right)\cdot F(2t)\sim min\left\{ \frac{f_{m}}{3},2f_{m} \right\}=\frac{f_{m}}{3}\\ \\
&\left[ f\left( \frac{t}{3} \right)*f(2t) \right]\cdot f(t)\leftrightarrow \frac{1}{2\pi}\left[ F\left( \frac{t}{3} \right)\cdot F(2t) \right]*F(t)\sim \frac{f_{m}}{3}+f_{m}\\ \\
&\therefore y(t)\sim f_{m}'=\frac{4}{3}f_{m}\\ \\
&f'_{m}\leq f_{c}\leq f_{s}-f_{m}'
\end{align}
\]
内插公式
假设\(f_{s}=2f_{m},\omega_{c}=\omega_{m}\):
\[\begin{align}
&F(j\omega)=F(j\omega)\cdot H(j\omega)\leftrightarrow f(t)=f_{s}(t)*h(t)\\ \\
&H(j\omega)=\begin{cases}
T_{s}\quad |\omega|\leq \omega_{m}\\ \\
0\quad | \omega|>\omega_{m}
\end{cases}=T_{s}g_{2\omega_{m}}(\omega)\leftrightarrow h(t)=T_{s} \frac{\sin \omega_{m}t}{\pi t}=Sa(\omega_{m}t)\\ \\
\implies f(t)&=f_{s}(t)*h(t)=\sum_{n=-\infty}^{+\infty}f(nT_{s})\delta(t-nT_{s})*Sa(\omega_{m}t)\\ \\
&=\sum_{n=-\infty}^{+\infty}f(nT_{s})Sa[\omega_{m}(t-nT_{s})]
\end{align}
\]
- 其中,\(Sa[\omega_{m}(t-nT_{s})]\)称为内插函数
- 在恢复原信号的时候,抽样时刻\(t=nT_s\)的值由抽样值\(f(nT_{s})\)确定,抽样时刻之外的信号值是无穷项内插函数的加权和
- 内插函数在取\(kT_{s}\)时,只有\(nT_{s}\)时为1,其余时刻为0,因此不同的内插函数求和时不会影响\(kT_{s}\)的值














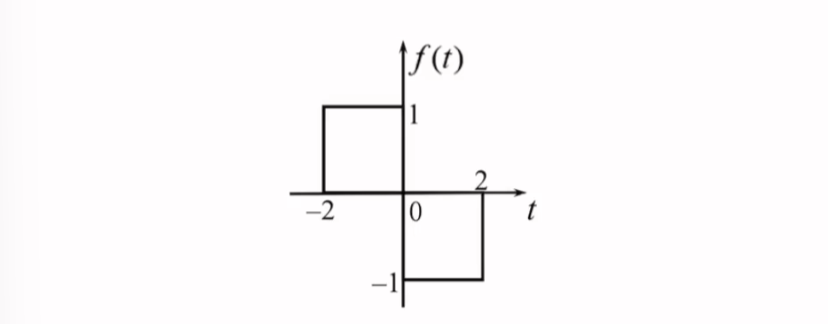
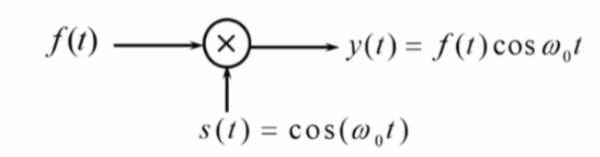
















 浙公网安备 33010602011771号
浙公网安备 33010602011771号