Update
- 2025.8.25
- 2025.8.26
- 2025.8.27
- 2025.8.28
- 2025.8.29
- 2.4 卷积积分 part2
- 2.4* 互相关函数与自相关函数
2.1 系统微分方程的经典解
微分方程的基本概念
对于单输入单输出的\(LIT\)连续系统来说,描述其输入-输出关系 的数学模型是\(n\)阶常系数线性微分方程,一般形式为:
\[a_{n}y^{(n)}(t)+a_{n-1}y^{(n-1)}(t)+\dots+a_{1}y'(t)+a_{0}y(t)=b_{m}e^{(m)}(t)+b_{m-1}e^{(m-1)}(t)+\dots+b_{1}e'(t)+b_{0}e(t)
\]
\[\sum_{i=0}^{n}a_{i}y^{(i)}(t)=\sum_{j=0}^{m}b_{j}e^{(j)}(t)
\]
- 初始条件:\(n\)阶系统在\(t=0\)时候接入激励,响应在\(t=0_{+}\)时刻的值:
\[y^{(j)}(0_{+})\ (j=0,1,2,\dots,n-1)
\]
- 初始状态:\(n\)阶系统在激励 没有接入的\(t=0\)时刻的响应值,该 值反映了系统的历史情况,与激励无关:
\[y^{(j)}(0_{-})\ (j=0,1,2,\dots,n-1)
\]
微分方程的经典解
齐次解\(y_{h}(t)\)
- 微分方程右侧为零时称为齐次方程,即\(\sum_{i=0}^{n}a_{i}y^{(i)}(t)=0\)
- 齐次解指齐次方程的解,只由系统的特征根决定
\(n\)阶微分方程的齐次解
\[y^{(n)}(t)+a_{n-1}y^{(n-1)}(t)+\dots+a_{0}y(t)=0
\]
特征方程:
\[\lambda^{n}+a_{n-1}+\lambda^{n-1}+\dots+a_{1}\lambda+a_{0}=0
\]
其中\(\lambda_{i}\)为方程的特征根
- 特征根均为单根:\(y_{h}(t)=\sum_{i=1}^{n}C_{i}e^{\lambda_{i}t}=C_{1}e^{\lambda_{1}t}+C_{2}e^{\lambda_{2}t}+\dots+C_{n}e^{\lambda_{n}t}\)
- 特征根含有\(r\)重根\(\lambda_{i}\):\(r\)重根对应\((C_{1}t^{r-1}+C_{2}t^{r-2}+\dots+C_{r-1}t+C_{r})e^{\lambda_{i}t}\)
- 特征根 含共轭复根\(\lambda_{1,2}=\alpha\pm j\beta\):共轭复根对应的解为:
- \(e^{\alpha t}[C_{1}\cos \beta t+C_{2}\sin \beta t]\)
- \(Ae^{\alpha t}\cos(\beta t-\theta),Ae^{j\theta}=C_{1}+jC_{2}\)(辅助角公式)
\(n\)阶微分方程的特解\(y_{p}(t)\)
形如\(y''+py'+qy=e^{\lambda x}P_{m}(x)\):
设特解形如:\(y^{*}=x^{k}e^{\lambda x}Q_{m}(x)\)
其中\(Q_{m}(x)\)为一个待定的\(m\)次多项式
\[k=
\begin{cases}
0\ ,\ \lambda不是特征根\\ \\
1\ ,\ \lambda是单特征根\\ \\
2\ ,\ \lambda是二重特征根
\end{cases}
\]
将\(y^{*}\)回带原微分方程确定系数即可
形如\(y''+py'+qy=e^{\lambda x}[P_{l}(x)\cos \omega x+P_{n}(x)\sin \omega x]\):
设特解形如\(y^{*}=x^{k}e^{\lambda x}[Q_{1}(x)\cos \omega x+Q_{2}(x)\sin \omega x]\)
其中\(Q_{1}(x),Q_{2}(x)\)为待定\(m\)次多项式,\(m=max\{ l,n \}\)
\[k=\begin{cases}
0\ ,\ \lambda\pm j\omega不是特征根\\ \\
1\ ,\ \lambda\pm j\omega是特征根
\end{cases}
\]
将\(y^{*}\)回带原微分方程确定系数即可
\(n\)阶微分方程的全解\(y(t)\)
- \(y(t)=y_{h}(t)+y_{p}(t)\)
- 此时齐次解中还有待定系数\(C_{i}\),\(n\)阶微分方程需要利用\(n\)个初始条件\(y(0_{+}),y'(0_{+}),\dots,y^{(n-1)}(0_{+})\)来确定
- 齐次解\(y_{h}(t)\)又被称作自由响应
- 特解\(y_{p}(t)\)又被称作强迫响应
自由响应与强迫响应
- 自由响应:仅与系统本身特性有关,而与激励的形式无关,其次解仅与系统特征根有关,特征根成为系统的“固有频率”,齐次解常称为系统的固有响应或自由响应
- 强迫响应:与激励的函数形式有关,特解的形式与激励的形式有关,常称为强迫响应
暂态响应和稳态响应
-
暂态响应:指响应中暂时出现的分量,随着时间增长\(t\to \infty\),它将消失\(\to 0\)
-
稳态响应:指稳定的分量,常以阶跃函数\(\varepsilon(t)\)和周期函数\(\sin \omega t,\cos \omega t\)等形式存在
-
对于\(LTI\)连续系统的微分方程\(y''(t)+5y'(t)+6y(t)=\varepsilon(t)\)以及全响应\(y(t)=-e^{-2t}+3\)
- 暂态响应为\(-e^{-2t}\),稳态响应为\(3\)
- 自由响应为\(-e^{-2t}\),强迫响应为\(3\)
初始状态和初始条件的讨论
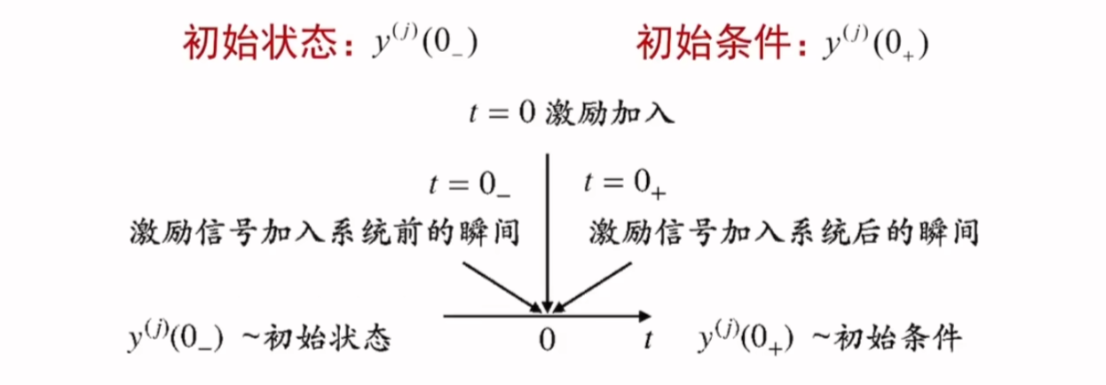
- 实际中,往往先得知系统的初始状态,即先得知激励接入前系统的历史信息
- 由于激励的接入,从\(0_{-}\)时刻过渡到\(0_{+}\)时刻之后,初始状态和初始条件往往不一样,我们用跳变量表示这个变化
- 求解微分方程需要从已知的初始状态\(y^{(j)}(0_{-})\)求得初始条件\(y^{(j)}(0_{+})\)
基本思路
- 如果激励加入后,在方程右端出现\(\delta(t)\)及其各阶导数,则在方程左端也应有与之对应的\(\delta(t)\)及其各阶导数项,使方程两段平衡
- 冲激函数的产生,意味着方程左端\(y^{d(i)}(t)\)中的某些项在\(t=0\)处有阶跃的跳变
- 两种求解初始条件的主要方法:待定系数法和冲激平衡法,后续做题主要使用后者
例
某\(LTI\)连续系统的微分方程为\(y''(t)+4y'(t)+3y(t)=e''(t)+2e'(t)+e(t)\),已知系统激励\(e(t)=\varepsilon(t)\),系统的初始状态为\(y(0_{-})=0,y'(0_{-})=1\),试求系统的初始条件\(y(0_{+}),y'(0_{+})\)
法1:待定系数法
\[\begin{align}
&设y''(t)=\delta'(t)+a\delta(t)+\varepsilon(t)\\ \\
&积分得y'(t)=\delta(t)+a\varepsilon(t)\quad y(t)=\varepsilon(t)\\ \\
&带入原微分方程,只关注冲激项得:\\ \\
&\delta'(t)+(4+a)\delta(t)=\delta'(t)+2\delta(t)\\ \\
&对比得4+a=2\to a=-2\\ \\
&则\begin{cases}
y'(t)=\delta(t)-2\varepsilon(t)\\ \\
y(t)=\varepsilon(t)
\end{cases}\\ \\
&\begin{cases}
y'(0_{+})=y'(0_{-})+y_{e}'(0_{+})=1-2=-1\\ \\
y(0_{+})=y(0_{-})+y_{e}(0_{+})=0+1=1
\end{cases}
\end{align}
\]
法2:冲激平衡阵列
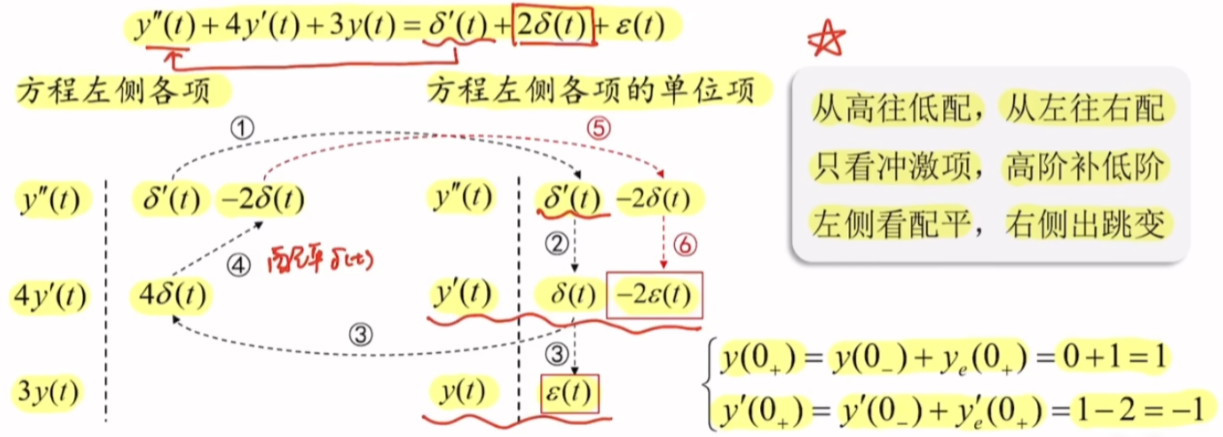
暂时还听不懂这部分,等明白了再回来重新写
2.2 零输入响应与零状态响应
零输入响应\(zero\ input:y_{zi}(t)\)
- 零输入响应指的是激励为零\(e(t)=0\)时,仅由初始状态引起的响应
- 由于激励为零,因此\(y_{zi}(t)\)对应的齐次方程\(\sum_{i=0}^{n}a_{i}y^{(i)}(t)=0\)
- 零输入响应由特征根决定,形式为齐次解。当特征根均为单实根时,零输入的响应形式为:
\[y_{zi}(t)=\sum_{i=1}^{n}C_{xi}e^{\lambda_{i}t},t\geq 0
\]
- 确定待定系数\(C_{xi}\):由初始状态\(y^{(j)}(0_{-})\)确定,由于没有激励,此时系统的初始状态就是零输入响应的初始条件,即\(y_{zi}^{(j)}(0_{+})=y^{(j)}(0_{-})\)
零状态响应\(zero\ state: y_{zs}(t)\)
- 零状态响应指的在初始状态为零时,仅由激励引起的响应
- 此时\(y_{zs}(t)\)对应非齐次方程\(\sum_{i=0}^{n}a_{i}y^{(i)}(t)=\sum_{j=0}^{m}b_{j}e^{(j)}(t)\)
- 零状态响应包含响应的齐次解和特解两部分,当特征根均为单实根时,零状态响应的形式为:
\[y_{zs}(t)=\sum_{i=1}^{n}C_{si}e^{\lambda_{i}t}+y_{p}(t)\quad t>0
\]
- 确定待定系数\(C_{si}\):
- 由零状态初始条件\(y_{zs}^{(j)}(0_{+})\)确定
- \(y_{zs}^{(j)}(0_{+})=跳变量\),通过冲激平衡法确定
全响应
\[y(t)=y_{h}(t)+y_{p}(t)=y_{zi}(t)+y_{zs}(t)
\]
\[\sum_{i=1}^{n}C_{i}e^{\lambda_{i}t}+y_{p}(t)=\sum_{i=1}^{n}C_{xi}e^{\lambda_{i}t}+\sum_{i=1}^{n}C_{si}e^{\lambda_{i}t}+y_{p}(t)\ ,\ t>0
\]
- 对于\(\sum_{i=1}^{n}C_{i}e^{\lambda_{i}t}+y_{p}(t)\),初始条件=初始状态+跳变量
- 对于\(\sum_{i=1}^{n}C_{xi}e^{\lambda_{i}t}\),初始条件=初始状态
- 对于\(\sum_{i=1}^{n}C_{si}e^{\lambda_{i}t}+y_{p}(t)\),初始条件=跳变量
辨析:待定系数\(C_{xi},C_{si}\)与齐次解待定系数\(C_{i}\)的区别:
- 零输入响应包含一部分齐次解,零状态响应包含另一部分齐次解以及特解
- 待定系数满足\(C_{i}=C_{xi}+C_{si}\)
求解思路总结
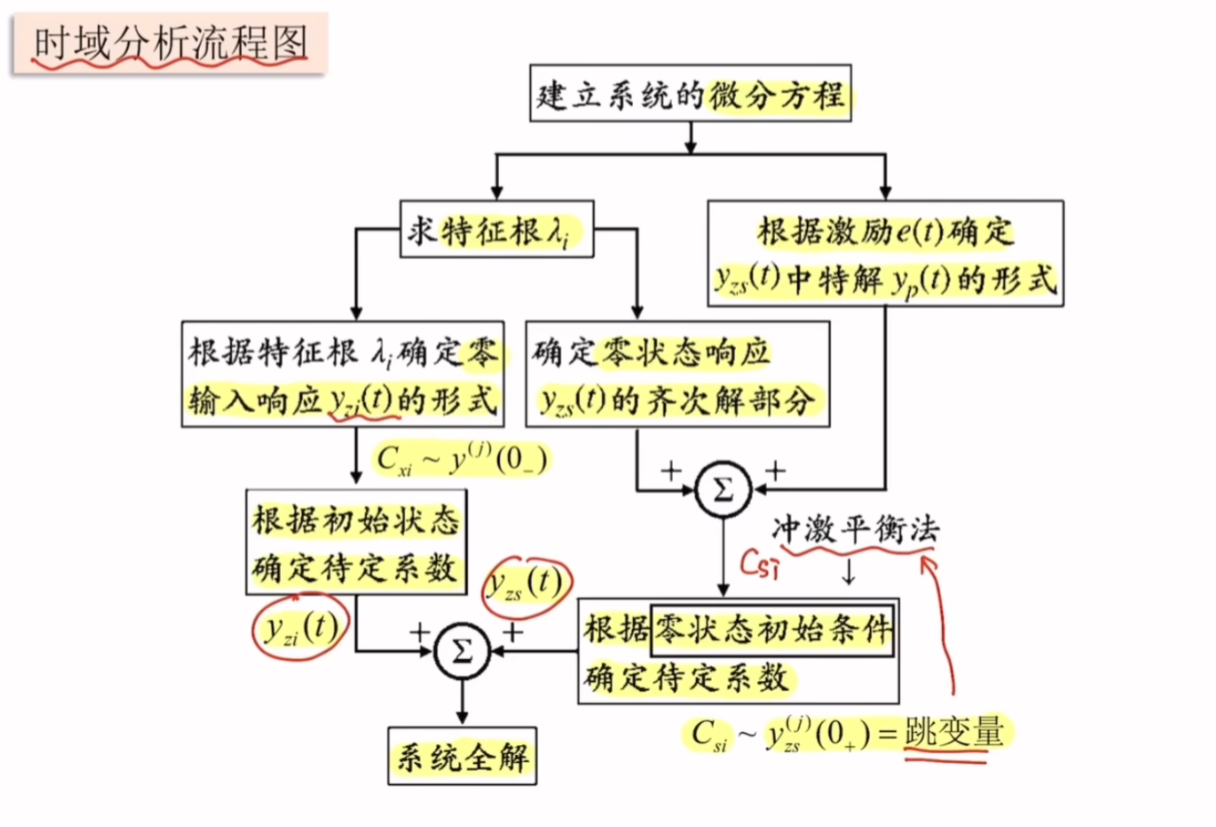
例
某\(LTI\)连续系统的微分方程为\(y''(t)+3y'(t)+2y(t)=\delta'(t)+2\delta(t)+3\varepsilon(t)+4t\cdot\varepsilon(t)\),初始状态\(y(0_{-})=1,y'(0_{-})=3\),求系统的零输入响应\(y_{zi}(t)\),零状态响应\(y_{zs}(t)\),与全响应\(y(t)\)
\[\begin{align}
&求y_{zi}(t):\\ \\
&齐次方程y''(t)+3y'(t)+2y(t)=0的特征方程为:\\ \\
&r^{2}+3r+2=0\ ,\ r_{1}=-1,r_{2}=-2\\ \\
&y_{zi}(t)=C_{1}e^{-t}+C_{2}e^{-2t}\\ \\
&带入初始状态得:\begin{cases}
C_{1}+C_{2}=1\\ \\
-C_{1}-C_{2}=3
\end{cases}\\ \\
&解得C_{1}=5,C_{2}=-4\\ \\
&\therefore y_{zi}(t)=(5e^{-t}-4e^{-2t})\varepsilon(t)
\end{align}
\]
\[\begin{align}
&求y_{zs}(t):\\ \\
&设特解y^{*}=At+B\ ,\ (y^{*})'=A\\ \\
&带入原微分方程得A=2,B=-\frac{3}{2}\\ \\
&则y_{zs}(t)=\left( C_{1}e^{-t}+C_{2}e^{-2t}+2t-\frac{3}{2} \right)\varepsilon(t)
\end{align}
\]
列冲激平衡阵列:
| 代入区 |
配凑区 |
积分区 |
积分区 |
| \(y''\) |
\(\delta'(t)-\delta(t)\) |
\(\delta'(t)\) |
\(-\delta(t)\) |
| \(3y'\) |
\(3\delta(t)\) |
\(\delta(t)\) |
\(-\varepsilon(t)\) |
| \(2y\) |
|
\(\varepsilon(t)\) |
|
\[\begin{align}
&由冲激平衡阵列得:\\ \\
&\begin{cases}
y_{zs}(0_{+})=1\\ \\
y'_{zs}(0_{+})=-1
\end{cases} \ ,\ 代入y_{zs}(t)得:\\ \\
&\begin{cases}
C_{1}+C_{2}-\frac{3}{2}=1\\ \\
-C_{1}-2C_{2}=-3
\end{cases}\\ \\
&解得C_{1}=2,C_{2}=\frac{1}{2}\\ \\
&则y_{zs}(t)=\left( 2e^{-t}+\frac{1}{2}e^{-2t}+2t-\frac{3}{2} \right)\varepsilon(t)\\ \\
&\therefore y(t)=y_{zi}(t)+y_{zs}(t)=\left( 7e^{-t}-\frac{7}{2}e^{-2t}+2t-\frac{3}{2} \right)\varepsilon (t)
\end{align}
\]
本题为我自己编写的,如果有问题欢迎及时指出!
2.3 单位冲激响应与单位阶跃响应
单位冲激响应\(h(t)\)
单位冲激信号的定义
\[h(t)=T[\{ x(0)=0 \},\{ e(t)=\delta(t) \}]
\]
- 激励为冲激信号\(\delta(t)\)时,\(LTI\)系统的零状态响应称为单位冲激响应,记为\(h(t)\)
单位冲激响应的形式
设方程左边\(y^{(n)}(t)\)为导数最高阶项,\(e^{(m)}(t)\)为导数最高阶项:
- \(n>m\):
- \(h(t)=\left( \sum_{i=1}^{n}C_{i}e^{\lambda_{i}t} \right)\varepsilon(t)\)
- 单位冲激响应与齐次解形式完全一致
- \(n=m\):
- \(h(t)=C_{0}\delta(t)+\left( \sum_{i=1}^{n}C_{i}e^{\lambda_{i}t} \right)\varepsilon(t)\)
- 依据冲激平衡,多出冲激项
- \(n<m\):
- \(C_{0}\delta(t)+C_{0(1)}\delta'(t)+\dots+C_{0(n-m)}\delta^{(n-m)}(t)+\left( \sum_{i=1}^{n}C_{i}e^{\lambda_{i}t} \right)\varepsilon(t)\)
\[初始状态h^{(j)}(0_{-}) \xrightarrow{冲激平衡法}初始条件h^{(j)}(0_{+})=跳变量
\]
例
某\(LTI\)连续系统的微分方程为\(y''(t)+5y'(t)+6y(t)=e'''(t)+2e'(t)\),求系统的单位冲激响应\(h(t)\)
\[\begin{align}
&已知:h''(t)+5h'(t)+6h(t)=\delta'''(t)+2\delta'(t)\\ \\
&齐次方程对应的特征方程为:r^{2}+5r +6=0,r_{1}=-2,r_{2}=-3\\ \\
&齐次解为C_{1}e^{-2t}+C_{2}e^{-3t}\\ \\
\end{align}
\]
列冲激平衡阵列:
| 代入区 |
配凑区 |
积分区 |
积分区 |
积分区 |
积分区 |
| \(h''\) |
\(\delta'''-5\delta''+21\delta'-75\delta\) |
\(\delta'''\) |
\(-5\delta''\) |
\(+21\delta'\) |
\(-75\delta\) |
| \(5h'\) |
\(5\delta''-25\delta'+105\delta\) |
\(\delta''\) |
\(-5\delta'\) |
\(+21\delta\) |
\(-75\varepsilon\) |
| \(6h\) |
\(6\delta'-30\delta\) |
\(\delta'\) |
\(-5\delta\) |
\(+21\varepsilon\) |
|
\[\begin{align}
&由冲激平衡阵列可知:h(0_{+})=21,h'(0_{+})=-75\\ \\
&代入原方程得:\begin{cases}
C_{1}+C_{2}=21\\ \\
-2C_{1}-3C_{2}=-75
\end{cases}\\ \\
&解得:C_{1}=-12,C_{2}=33\\ \\
&则h(t)=(-12e^{-2t}+33e^{-3t})\varepsilon(t)+\delta'(t)-5\delta'(t)
\end{align}
\]
- 注意最后计算\(h(t)\)的时候,需要将冲激平衡阵列中的最后一行的变量加上!!
单位阶跃响应\(g(t)\)
单位阶跃响应的定义
\[g(t)=T[\{ x(0)=0 \},\{ e(t)=\varepsilon(t) \}]
\]
- 激励为单位阶跃信号\(\varepsilon(t)\)时,\(LTI\)系统的零状态响应称为单位阶跃响应,记为\(g(t)\)
- 此时微分方程对应非齐次方程,单位阶跃响应可能包含特解,按照求解一般零状态响应的思路做即可
\(h(t)\)与\(g(t)\)的关系
\[\begin{align}
&\begin{cases}
h(t)=T[\{ x(0)=0 \},\{ e(t)=\delta(t) \}] =F(\delta(t))\\ \\
g(t)=T[\{ x(0)=0 \},\{ e(t)=\varepsilon(t) \}]=F(\varepsilon(t))
\end{cases}\\ \\
&由于T为LTI系统,具有线性性质,且\delta(t)=\varepsilon'(t)\\ \\
&则h(t)=F(\delta(t))=F(\varepsilon'(t))=F'(\varepsilon(t))=g'(t)\\ \\
&同理,由于\varepsilon(t)=\int_{-\infty}^{t}\delta(x)dx\\ \\
&则g(t)=F(\varepsilon(t))=F\left( \int_{-\infty}^{t}\delta(x)dx \right)=\int_{-\infty}^{t}F(\delta(x))dx=\int_{-\infty}^{t}h(x)dx
\end{align}
\]
- \(h(t)=g'(t)\),\(g(t)=\int_{-\infty}^{t}h(x)dx\)
- 单位冲激响应完全由系统微分方程决定,可表征系统特性,可以用\(h(t)\),\(g(t)\)表征系统,判断系统的因果性、稳定性等特性
2.4 卷积积分
卷积积分的定义
\[f_{1}(t)*f_{2}(t)=\int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(t-\tau)d\tau
\]
- 积分式中,\(\tau\)是为了防止变量混淆而虚设的积分变量
- 卷积积分的最终结果是一个新的连续函数,自变量仍然为时间\(t\)
- 卷积积分实质上是一个关于位移量\(t\)的连续时间函数
换为算法竞赛中的卷积和来理解:
\[(f_{1}*f_{2})(t)=\sum_{i+j=t}f_{1}(i)\times f_{2}(j)
\]
实际上就是将求和换为了积分,本质上是离散与连续的区别
卷积积分的求解
解析法
关键: 依据信号的形式确定积分的区间,从而确定卷积结果的信号形式
- 若\(f_{1}(t)\)是因果信号,即\(f_{1}(t)=0,t<0\),\(f_{2}(t)\)不受限制,则:
\[f_{1}(t)*f_{2}(t)=\int_{0}^{+\infty}f_{1}(\tau)f_{2}(t-\tau)d\tau\quad \tau>0
\]
- 若\(f_{2}(t)\)是因果信号,即\(f_{2}(t)=0,t<0\),\(f_{1}(t)\)不受限制,则:
\[f_{1}(t)*f_{2}(t)=\int_{-\infty}^{t}f_{1}(\tau)f_{2}(t-\tau)d\tau\quad t-\tau>0\to \tau<t
\]
- 若\(f_{1}(t),f_{2}(t)\)均为因果信号,\(f_{1}(t)=f_{2}(t)=0,t<0\),则:
\[f_{1}(t)*f_{2}(t)=\int_{0}^{t}f_{1}(\tau)f_{2}(t-\tau)d\tau\quad \tau>0,t-\tau> 0\to 0<\tau<t
\]
例
\[\begin{align}
&1)计算t\varepsilon(t)*e^{-t}\varepsilon(t):\\ \\
解:&\\ \\
&\begin{cases}
\tau>0\\ \\
t-\tau>0
\end{cases}\to 0<\tau<t\\ \\
原式&=\int_{0}^{t}\tau e^{-t+\tau}d\tau=e^{-t}\int_{0}^{t}\tau e^{\tau}d\tau=e^{-t}\int_{0}^{t}\tau de^{\tau}\\ \\
&=e^{-t}\left[ \tau e^{\tau}\bigg|_{0}^{t}\varepsilon(t)-\int_{0}^{t}e^{\tau}d\tau \right]=e^{-t}[te^{t}-e^{t}+1]\varepsilon(t)\\ \\
&=(t-1+e^{-t})\varepsilon(t)
\end{align}
\]
\[\begin{align}
2)&计算\varepsilon(t+2)*\varepsilon(t-3):\\ \\
解:&\\ \\
&\begin{cases}
\tau+2>0\\ \\
t-\tau-3>0
\end{cases}\to-2<\tau<t-3\\ \\
& -2<t-3 \to t>1 \\ \\
原式&=\int_{-2}^{t-3}d\tau=(t-1)\varepsilon(t-1)
\end{align}
\]
- 需要特别注意,除了计算\(\tau\)的范围以确定积分上下限以外,还需要计算\(t\)的取值范围以确定最后的\(\varepsilon\)函数
- 经典结论 :\(\varepsilon(t)*\varepsilon(t)=t\varepsilon(t)\)
图解法
- 变量置换:\(f_{1}(t)\to f_{1}(\tau),f_{2}(t)\to f_{2}(\tau)\),作出\(f_{1}(\tau),f_{2}(\tau)\)的波形
- 波形反折:\(f_{2}(\tau)\to f_{2}(-\tau)\),作出关于纵轴翻折的波形
- 由于卷积具有交换律,翻转\(f_{1}(\tau)\)也可以
- 波形移位:\(f_{2}(-\tau)\to f_{2}(t-\tau)\),沿着\(\tau\)轴平移一个\(t\)的值,得到\(f_{2}(t-\tau)\)
- 函数相乘:将移位后的函数\(f_{2}(t-\tau)\)与\(f_{1}(\tau)\)相乘,得到卷积积分的被积函数\(f_{1}(\tau)f_{2}(t-\tau)\)
- 求解积分 :若\(f_{1}(\tau)\)与\(f_{2}(t-\tau)\)的波形有重叠,则卷积积分为重叠区间上的积分;若波形无重叠,则卷积积分为0
- 时间遍历:令\(t\)在\((-\infty,+\infty)\)内变化,重复上述步骤最终解出卷积
相关结论
该结论可以通过图解法推导
两个等宽的门函数卷积,结果为等腰三角形
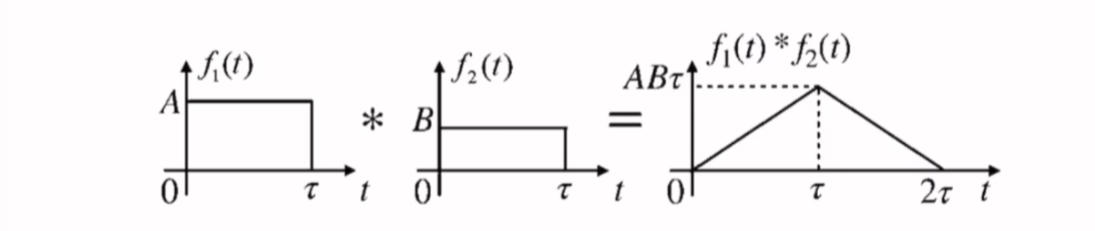
\[f_{1}(t)*f_{2}(t)=\begin{cases}
ABt\quad {0}\leq t<\tau\\ \\
AB(2\tau-t)\quad \tau\leq t\leq {2}\tau\\ \\
0\quad t\leq 0,t> 2\tau
\end{cases}
\]
- 三角形高度:两门函数幅度之积乘以门宽
- 三角形的底:门函数的宽度之和
- 时间范围:卷积积分的范围为两函数时间范围之和
两个不等宽的门函数的卷积,结果为等腰梯形
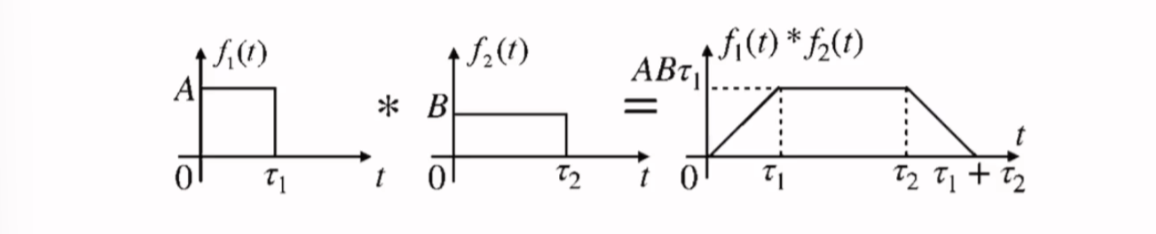
\[f_{1}(t)*f_{2}(t)=\begin{cases}
ABt\quad 0\leq t<\tau_{1}\\ \\
AB\tau_{1}\quad\tau_{1}\leq t<\tau_{2}\\ \\
AB(\tau_{1}+\tau_{2}-t)\quad \tau_{2}\leq t\leq \tau_{1}+\tau_{2}\\ \\
0\quad t< 0,t>\tau_{1}+\tau_{2}
\end{cases}
\]
- 梯形高度:两门函数幅度之积乘以 窄门门宽
- 梯形上底:门函数宽度之差的绝对值
- 梯形下底:门函数宽度之和
- 时间范围:卷积积分的范围为两函数时间范围之和
卷积积分的性质
任意信号的分解
\[f(t)\approx \hat{f(t)}=\sum_{n=-\infty}^{\infty}f(n\Delta)g_{\Delta}(t-n\Delta)\cdot \Delta
\]
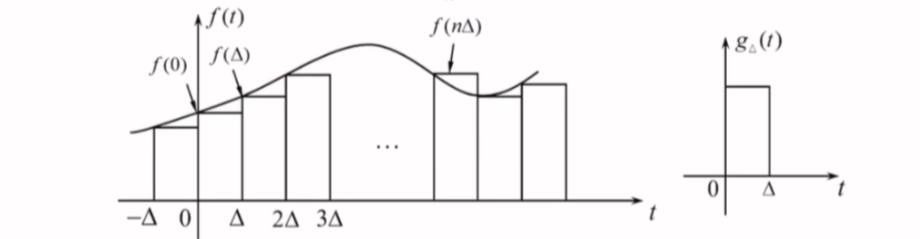
\(\Delta\to 0\)时:
- \(\Delta\to d\tau\),分割无限密集,变为无穷小量
- \(n\Delta\to \tau\),离散时间\(\to\)连续时间
- \(g_{\Delta}(t-n\Delta)\to \delta(t-\tau)\),门函数\(\to\)冲激信号
- \(f(n\Delta)\to f(\tau)\),离散取值\(\to\)连续函数
- \(\sum_{n=-\infty}^{+\infty}\to \int_{-\infty}^{+\infty}\)
\[f(t)=\lim_{ \Delta \to 0 }\sum_{n=-\infty}^{\infty}f(n\Delta)g_{\Delta}(t-n\Delta)\cdot \Delta=\int_{-\infty}^{+\infty}f(\tau)\delta(t-\tau)d\tau
\]
即:
\[f(t)=f(t)*\delta(t)
\]
- 任意信号可以用一系列单位冲激信号及其位移信号的线性组合表示
借助单位冲激响应与卷积积分求解系统的零状态响应
\[e(t)=\int_{-\infty}^{+\infty}e(\tau)\delta(t-\tau)d\tau
\]
\[\begin{align}
\begin{array}
&单位冲激响应:&\delta(t)\to h(t)\\ \\
时不变性:&\delta(t-\tau)\to h(t-\tau)\\ \\
齐次性:&e(\tau)\delta(t-\tau)\to e(\tau)h(t-\tau)\\ \\
叠加性:&\int_{-\infty}^{+\infty}e(\tau)\delta(t-\tau )d\tau
\to \int_{-\infty}^{+\infty}e(\tau)h(t-\tau)d\tau
\end{array}
\end{align}
\]
\[y_{zs}(t)=\int_{-\infty}^{+\infty}e(\tau)h(t-\tau)d\tau=e(t)*h(t)
\]
- 连续系统的零状态响应为激励信号和系统单位冲激响应的卷积积分
\[y_{zs}(t)=e(t)*h(t)
\]
代数性质
- 交换律:\(f_{1}(t)*f_{2}(t)=f_{2}(t)*f_{1}(t)\),卷积积分中反折函数可以任选
- 分配率:\(f_{1}(t)*[f_{2}(t)+f_{3}(t)]=f_{1}(t)*f_{2}(t)+f_{1}(t)*f_{3}(t)\)
- 结合律:\(f_{1}(t)*[f_{2}(t)*f_{3}(t)]=[f_{1}(t)*f_{2}(t)]*f_{3}(t)\)
复合系统的冲激响应
\[y_{zs}(t)=e(t)*h(t)
\]
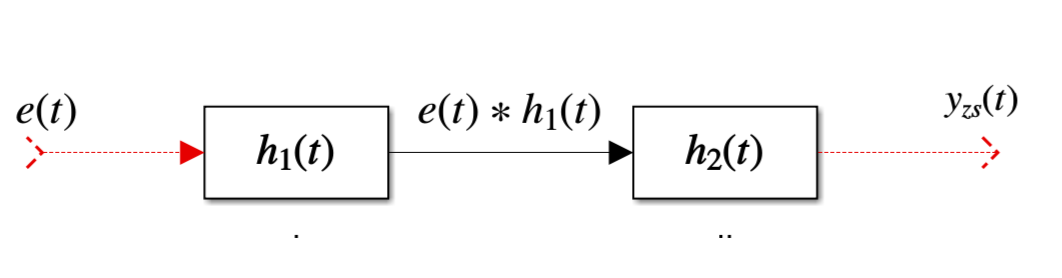
- \(h(t)=h_{1}(t)*h_{2}(t)\)
- \(n\)个级联子系统的 等效冲激相应为\(n\)个子系统冲激相应卷积
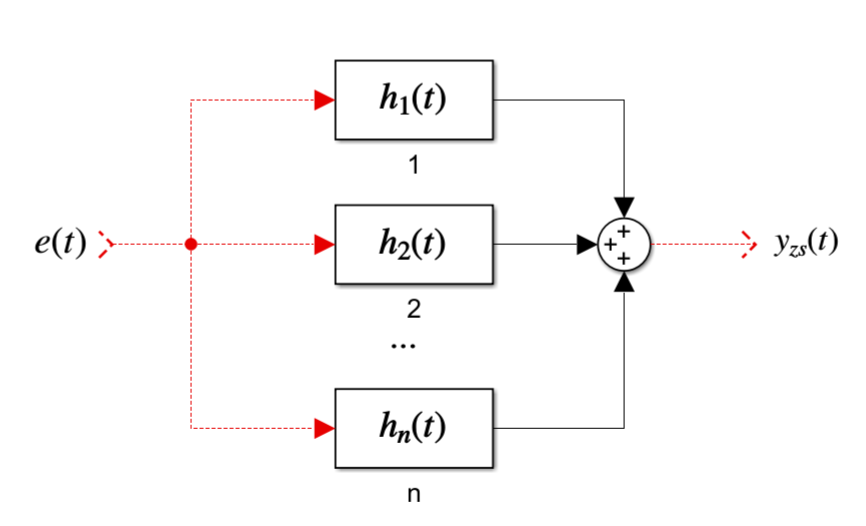
- \(h(t)=h_{1}(t)+h_{2}(t)+\dots+h_{n}(t)\)
- \(n\)个并联子系统的等效冲激响应为\(n\)个子系统的冲激响应之和
移位性质
\[\begin{align}{}
&f_{1}(t)*f_{2}(t-t_{0})=f_{1}(t-t_{0})*f(t)=f(t-t_{0}) \\ \\
&f(t-t_{1})*f_{2}(t-t_{2})=f_{1}(t-t_{2})*f_{2}(t-t_{1})=f(t-t_{1}-t_{2})
\end{align}
\]
- 参与卷积的两个函数,有一个移位,整体就会产生相同的移位
奇异函数的卷积特性
冲激信号的卷积
\[\begin{cases}
f(t)*\delta(t)=\delta(t)*f(t)\\ \\
f(t)*\delta(t-t_{0})=\delta(t-t_{0})*f(t)=f(t-t_{0})
\end{cases}
\]
- 函数卷积冲激函数等于其本身,卷积位移的冲激函数等于该函数本身进行移位:重现性质
冲激偶信号的卷积
\[\begin{align}
&f(t)*\delta'(t)=f'(t)\\ \\
&f(t)*\delta^{(n)}(t)=f^{(n)}(t)
\end{align}
\]
阶跃信号的卷积
\[f(t)*\varepsilon(t)=\int_{-\infty}^{+\infty}f(\tau)\varepsilon(t-\tau)d\tau=\int_{-\infty}^{t}f(\tau)d\tau
\]
利用卷积积分构造周期信号
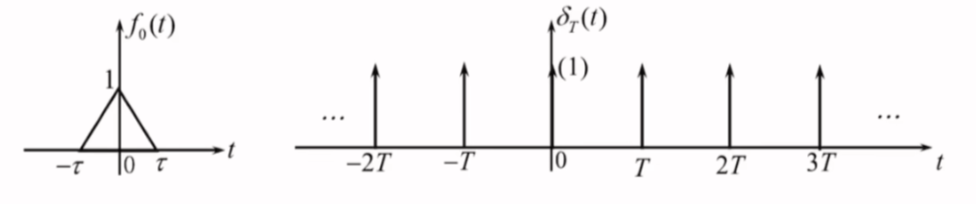
\[f_{T}(t)=f_{0}(t)*\delta_{T}(t)=f_{0}(t)*\sum_{n=-\infty}^{\infty}\delta(t-nT)=\sum_{n=-\infty}^{\infty}f_{0}(t-nT)
\]
- 可以利用第一个周期内的信号脉冲单体\(f_{0}(t)\)和周期为\(T\)的冲激串信号的卷积积分构造周期信号

卷积的微分与积分
\[\begin{align}
&微分性质:\frac{d}{dt}[f_{1}(t)*f_{2}(t)]=\frac{d}{dt}f_{1}(t)*f_{2}(t)=f_{1}(t)* \frac{d}{dt}f_{2}(t)\\ \\
&积分性质:\int_{-\infty}^{t}[f_{1}(x)*f_{2}(x)]dx=\int_{-\infty}^{t}f_{1}(x)dx*f_{2}(t)=f_{1}(t)*\int_{-\infty}^{t}f_{2}(x)dx
\end{align}
\]
- 对两个函数卷积积分的结果求导/积分,等于先对其中任一函数求导/积分后再卷积
\[微积分性质:f_{1}(t)*f_{2}(t)=\frac{d}{dt}f_{1}(t)*\int_{-\infty}^{t}f_{2}(x)dx=\int_{-\infty}^{t}f_{1}(x)dx* \frac{d}{dt}f_{2}(t)
\]
- 两个函数卷积积分的结果,等于先对其中任一函数求导,再对另一个函数积分,然后两个函数再卷积
例
1):
\[\begin{align}
&求e^{-2t}\varepsilon(t)*\delta''
(t-1)*[t\varepsilon(t)]: \\ \\
解:&\\ \\
原式&=e^{-2t}\varepsilon(t)*\int_{-\infty }^{t}dx \int_{-\infty}^{x}\delta''(y-1)dy\ * \frac{d^2}{dt^2}[t\varepsilon(t)]\\ \\
&=e^{-2t}\varepsilon(t)*\delta(t-1)*\delta(t)=e^{-2t}\varepsilon(t)*\delta(t-1)\\ \\
&=e^{-2t+2}\varepsilon(t-1)
\end{align}
\]
- 在注意到卷积函数中需要积分操作时,可以对其中一项积分另一项微分来转化 (卷积的微积分性质)
2):
已知某线性时不变系统的冲激响应\(h(t)=\cos t\cdot \varepsilon(t)\),\(e(t)\)为下图,求系统的零状态响应\(y_{zs}(t)\)

\[\begin{align}
&利用门函数可构造得e(t)=g_{\pi}(t)*g_{\pi}(t)=[\varepsilon(t)-\varepsilon(t-\pi)]*[\varepsilon(t)-\varepsilon(t-\pi)]\\ \\
y_{zs}(t)&=h(t)*e(t)=h^{(-2)}(t)*g_{\pi}'(t)*g_{\pi}'(t)\\ \\
&=h^{(-2)}(t)*[\delta(t)-\delta(t-\pi)]*[\delta(t)-\delta(t-\pi)]\\ \\
&=h^{(-2)}(t)*[\delta(t)-2\delta(t-\pi)+\delta(t-2\pi)]\\ \\
h^{(-2)}(t)&=\int_{-\infty}^{t}dt\int_{-\infty}^{x}\cos y\varepsilon(y)dy=\int_{-\infty}^{t}\sin x\varepsilon(x)dx\\ \\
&=(1-\cos t)\varepsilon(t)\\ \\
y_{zs}(t)&=(1-\cos t)\varepsilon(t)*[\delta(t)-2\delta(t-\pi)+\delta(t-2\pi)]\\ \\
&=(1-\cos t)\varepsilon(t)-2(1-\cos (t-\pi))\varepsilon(t-\pi)+(1-\cos(t-2\pi))\varepsilon(t-2\pi)\\ \\
&=(1-\cos t)\varepsilon(t)-2(1+\cos t)\varepsilon(t-\pi)+(1-\cos t)\varepsilon(t-2\pi)
\end{align}
\]
- 实际上直接画出\(e'(t)\)以及\(e''(t)\)的图像更容易做,上述过程采用的是门函数构造法
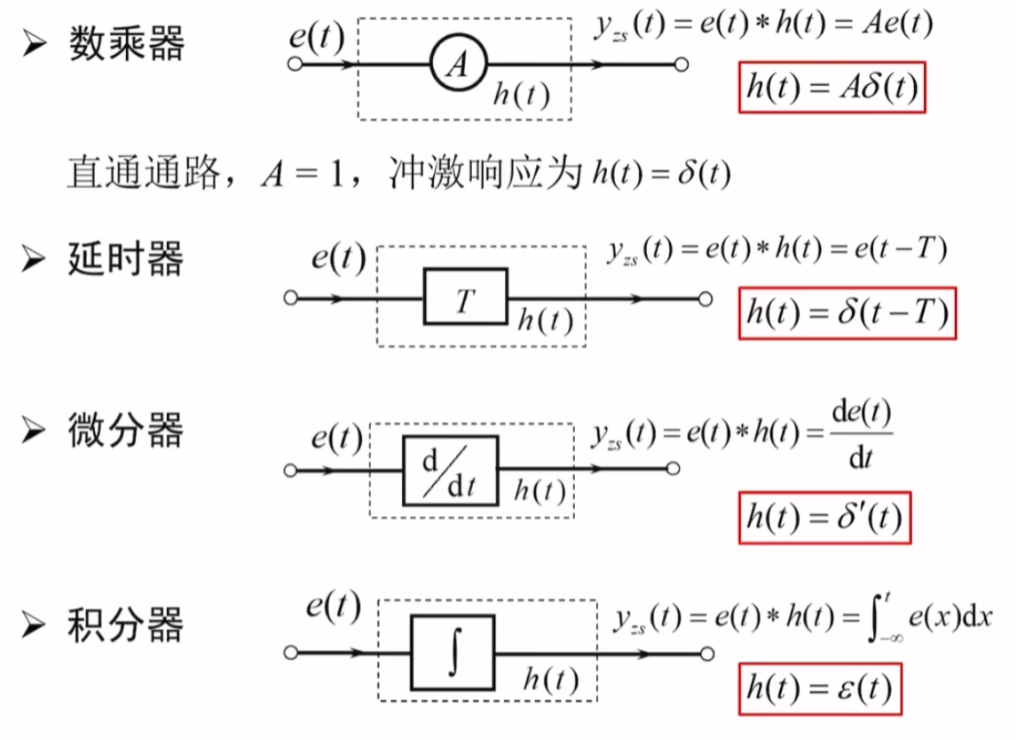
常用子系统的单位冲激响应
2.4* 互相关函数与自相关函数
互相关和自相关函数的定义
为了比较某信号与另一延时\(\tau\)信号之间的相似度,需要引入相关函数的概念,相关函数也称为相关积分,它与卷积的运算方法类似
互相关函数
已知实函数\(f_{1}(t),f_{2}(t)\)均为能量信号,则他们之间的互相关函数定义为:
\[\begin{align}
&R_{12}(\tau)=\int_{-\infty}^{+\infty}f_{1}(t)f_{2}(t-\tau)dt=\int_{-\infty}^{+\infty}f_{1}(t+\tau)f_{2}(t)dt\\ \\
&R_{21}(\tau)=\int_{-\infty}^{+\infty}f_{1}(t-\tau)f_{2}(t)dt=\int_{-\infty}^{+\infty}f_{1}(t)f_{2}(t+\tau)dt
\end{align}
\]
- 注意:角标中前面的信号领先时间\(\tau\)
- 互相关函数是两信号时间差\(\tau\)的函数
- 一般\(R_{12}(\tau)\neq R_{21}\)
- \(R_{12}(\tau)=R_{21}(-\tau)\)
自相关函数
如果实函数\(f_{1}(t),f_{2}(t)\)是同一个信号\(f(t)\),此时无需区分\(R_{12},R_{21}\),直接用\(R(t)\)表示,称为自相关函数
\[R(\tau)=\int_{-\infty }^{+\infty}f(t)f(t-\tau)dt=\int_{-\infty}^{+\infty}f(t+\tau)f(t)dt
\]
对自相关函数,有:
\[R(\tau)=R(-\tau)
\]
实函数的自相关函数是时移\(\tau\)的偶函数
相关与卷积的关系
\[\begin{align}
&卷积:f_{1}(t)*f_{2}(t)=\int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(t-\tau)d\tau\\ \\
&互相关:R_{12}(\tau)=\int_{-\infty}^{+\infty}f_{1}(t)f_{2}(t-\tau)dt\xrightarrow{t,\tau互换}R_{12}(t)=\int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(\tau-t)d\tau
\end{align}
\]
不同之处:卷积积分存在函数的反折,相关运算则不需要反折,其余移位、相乘积分的运算 方法相同
\[R_{12}(t)=\int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(\tau-t)d\tau=\int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}[-(t-\tau)]d\tau=f_{1}(t)*f_{2}(-t)
\]
因此,两个实偶函数的相关运算与卷积运算的结果相同



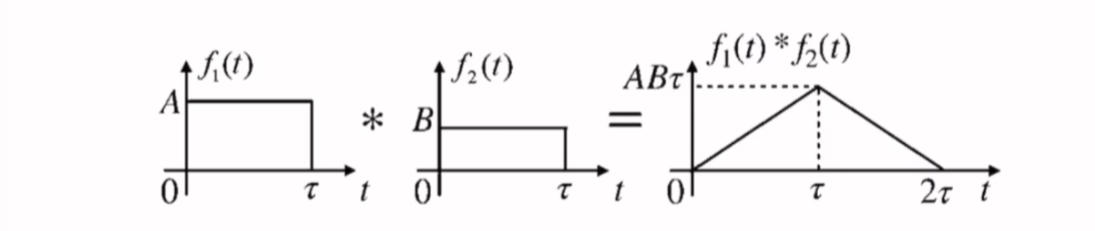
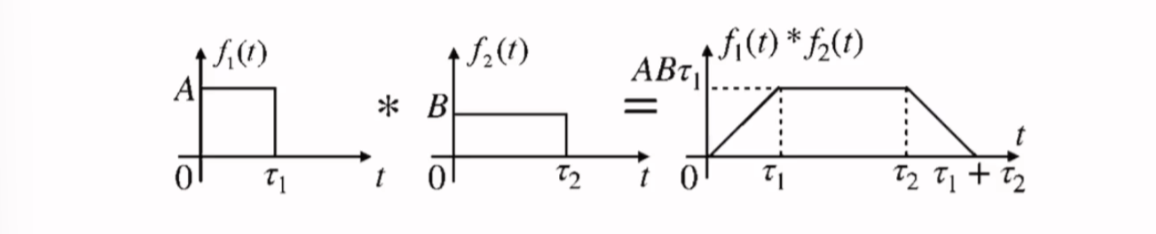









 浙公网安备 33010602011771号
浙公网安备 33010602011771号