[信号与系统个人笔记]第一章 信号与系统的基本概念
Update
- 2025.8.20
- 1.1信号的描述与分类
- 1.2基本信号与其时域特性 part1
- 2025.8.21
- 1.2基本信号与其时域特性 part2
- 2025.8.22
- 1.3 信号的基本运算
- 1.4 系统的描述与分类
- 2025.8.23
- 1.5 线性时不变系统的性质
1.1 信号的描述与分类
信号的描述
信号可以用函数解析式描述 ,也可以用波形图描述
信号的分类
确定信号和随机信号
- 确定信号可以用确定的函数 或者波形表示
- 随机信号要用概率密度、相关函数、谱密度等数学 模型进行分析(随机过程)
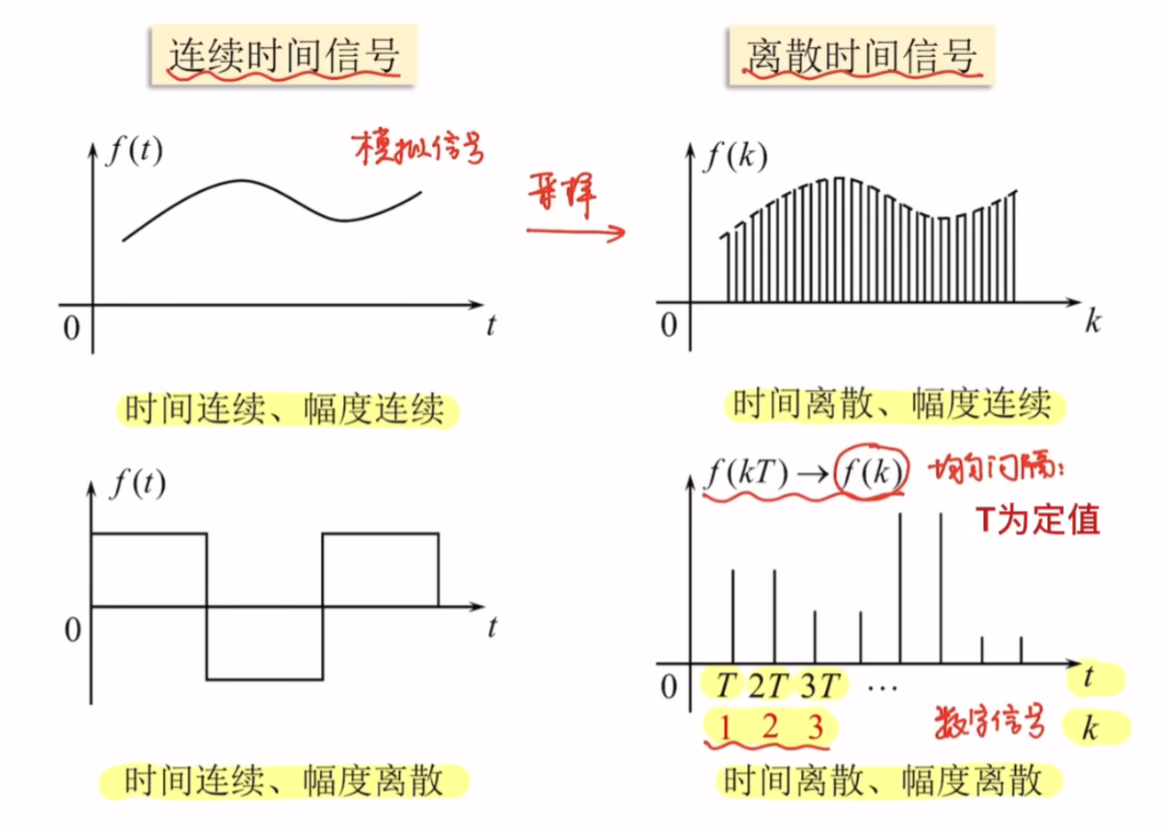
连续时间信号和离散时间信号
| 名称 | 时间取值 | 幅度取值 |
|---|---|---|
| 连续时间信号 | 连续(定义域) | 可以连续、可以不连续 |
| 离散时间信号 | 离散(定义域) | 可以连续、可以不连续 |
| 模拟信号 | 连续 | 连续 |
| 数字信号 | 离散 | 离散 |
- 时间连续或离散的含义是定义域的连续或离散,因此需要和数学中的概念作区分
周期信号和非周期信号
周期信号指的是每隔一定时间\(T\)(或者整数\(N\))按相同规律重复变化的信号
- 连续周期信号:\(f(t)=f(t+mT),m=0,\pm 1,\pm 2,\dots\)
- 离散周期信号:\(f(t)=f(t+mN),m=0,\pm 1,\pm 2,\dots\)
非周期信号不具备周期性,令周期信号的周期趋于无穷大\(T\to \infty\),则周期信号变为非周期信号
两个连续周期信号之和的周期性判定
- 若两个连续信号的周期之比为有理数,设\(\frac{T_{1}}{T_{2}}=\frac{P}{Q}\),其中\(P,Q\)为互质的整数,则和信号为周期信号,周期为\(T_{1},T_{2}\)的最小公倍数\(lcm(T_{1},T_{2})\)
例1
判断下列信号是否是周期信号,如果是则求其周期:
\(1)f(t)=\sin \pi t+2\cos{2}t\quad 2)f(t)=\sin{2}t+\cos 3t\)
解:
对于1),由于第一项的周期不含\(\pi\),而第二项含有\(\pi\),其周期之比为无理数,故不是周期信号;
对于2),\(T_{1}=\pi,T_{2}=\frac{2\pi}{3}, \frac{T_{1}}{T_{2}}=\frac{3}{2},T=2T_{1}=2\pi\)
能量信号与功率信号
信号的能量与功率
设信号的能量为\(E\),功率为\(P\):
对于连续信号而言:
- 能量即对信号的模的平方积分,考虑到存在复数信号,所以不写成\(f^2(t)\)
- 功率即能量除以时间,取一段时间\(T\),计算在这段时间内的能量积分\(E_{T}\),平均功率即\(\frac{E_{T}}{T}\),令\(T\to \infty\)即可得到平均功率
对于离散信号而言:
- 这与连续信号的两个表达式非常相似,积分换为求和即可
- 注意功率的分母为\(2N+1\),这是因为\(\sum_{k=-N}^{N}\)中求和了\(2N+1\)个点,1来自于\(k=0\)一点
能量信号与功率信号
- 能量信号:能量为有界值,即\(0<E<+\infty\),由功率的定义极限可知,分子有界分母无穷,此时功率为\(P=0\)
- 功率信号:功率为有界值,即\(0<P<+\infty\),由功率的定义极限可知,分母为无穷且极限存在,则分子必为无穷,即\(E=\infty\)
结论:周期信号都是功率信号,时域有限信号都是能量信号!
特别地,有些信号既不是能量信号,也不是功率信号,如\(f(t)=e^{-t}\)
例2
判断下列信号是能量信号还是功率信号,并求能量或功率
-
\(f(t)=10\cos(3t-\theta)\)
- 余弦函数为周期函数,必然是功率信号
- 由高中知识我们知道,交流电\(I=A\sin(\omega t+k)\)的有效值为\(\hat{I}=\frac{A}{\sqrt{ 2 }}\),则功率可以使用有效值计算:\(P=\hat{I}^2R=\hat{I}^2·1\Omega=\frac{A^2}{2}\)
- 因此\(P=\frac{A^2}{2}=50W\)
- 该结论适用于所有正余弦信号!
- 当然本题也可以直接套定义进行积分,化二倍角即可
-
\(f(t)=10e^{-5t},t\geq 0\)
-
\[E=\int_{-\infty}^{+\infty}f^2(t)dt=\int_{0}^{+\infty}100e^{ -10t }dt=100\left[ -\frac{1}{10}e^{ -10t } \right]_{0}^{+\infty}=10J \]
- 因此为能量信号
- 注意定义式中的\(\int_{-\infty}^{+\infty}\),与概率论中的积分类似,需要看实际的\(f(t)\)的定义域来变换积分上下限
- 注意若此处没有\(t\geq0\)的限制,则既不是能量信号又不是功率信号
- 结论:单边衰减信号为能量信号
-
-
\(f(k)=2,k\geq 0\)
-
\[E=\lim_{ N \to \infty }\sum_{k=-N}^N|f(k)|^2=\lim_{ N \to \infty }\sum_{k=0}^N 4=4\lim_{ N \to \infty }(N+1)=\infty \]
-
\[P=\lim_{ N \to \infty } \frac{1}{N+1}·4(N+1)=4W \]
- 因此为功率信号
- 注意变量为\(k\)的时候,代表离散时间信号
- 注意功率除的时间是灵活变化的,具体要看\(\sum\)中求和了多少个点
-
1.2 基本信号及其时域特性
常见连续信号
指数信号
指数信号对时间求导、积分仍然是指数信号
正弦信号
周期\(T\),角频率\(\omega\),频率\(f\),则有:
正弦信号对时间求导、积分仍然是正弦信号
根据欧拉公式:
其中\(j\)为虚数单位\(i\)
从而:
复指数信号
- 其中\(s=\sigma+jw\),为一个复数
- \(\sigma\)决定增长或衰减
- \(\omega\)决定震荡的快慢
复指数信号的不同情形
- \(\sigma=0,\omega\neq 0\):实部和虚部均为等幅振荡,\(f(t)=K(\cos \omega t+j\sin \omega t)\)
- \(\sigma\neq 0,\omega\neq 0\):实部和虚部均为增长或衰减震荡,\(f(t)=Ke^{ \sigma t }(\cos\omega t+j\sin \omega t)\)
- \(\sigma\neq 0,\omega=0\):实指数信号,\(f(t)=Ke^{ \sigma t }\)
- \(\sigma=0,\omega\neq 0\):虚指数信号,\(f(t)=K(\cos \omega t+j\sin \omega t)=Ke^{ j\omega t }\)
- \(\sigma=\omega=0\):直流信号,\(f(t)=K\)
抽样信号
- \(Sample\to Sa\),可以读作“萨”
- \(Sa(\omega_{0}t)=\frac{\sin \omega_{0}t}{\omega_{0}t}\)
抽样信号的性质
- \(Sa(t)\)为\(t\)的偶函数
- \(\lim_{ t \to 0 }Sa(t)=\lim_{ t \to \infty } \frac{\sin t}{t}=1,\lim_{ t \to \infty }Sa(t)=0\)
- 过零点:\(t=n\pi,n=\pm 1,\pm 2,\dots\)
- \(\int_{0}^{+\infty}Sa(t)dt=\int_{-\infty}^0Sa(t)dt=\frac{\pi}{2}\)
- \(\int_{-\infty}^{+\infty}Sa(t)=\pi\)
奇异信号
函数本身或其导数、积分有不连续点(即跳变点)的信号
单位斜变信号\(r(t)\)
- 小于0的部分全是0
- 大于0的部分是\(y=x\)
单位阶跃信号\(\varepsilon(t)\)
- \(\varepsilon(t)\)在\(t=0\)处的函数值没有定义
\(r(t)\)与\(\varepsilon(t)\)的关系
- \(r(t)=t·\varepsilon(t)\)
- \(\varepsilon(t)=\frac{d\ r(t)}{dt}\)
- \(r(t)=\int_{-\infty}^t\varepsilon(x)dx\)
单位阶跃信号的物理意义
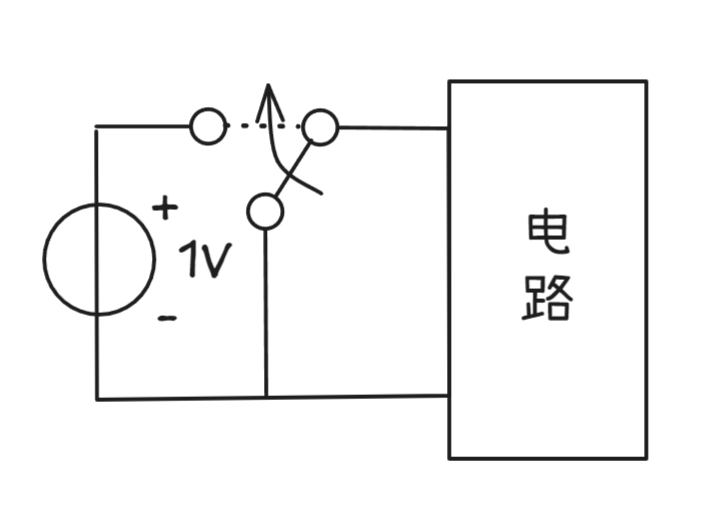
阶跃函数描述了信号的接入特性
- \(\varepsilon(t)\)表示信号\(f(t)=1\)在\(t=0\)的时刻接入系统
- \(f(t)\varepsilon(t)\)表示信号\(f(t)\)在\(t=0\)的时刻接入系统
- \(f(t)\varepsilon(t-t_{0})\)表示信号\(f(t)\)在\(t=t_{0}\)的时刻接入系统
体现在波形上位跳变点或者波形的起始和终止
宽度为\(\tau\)的门函数
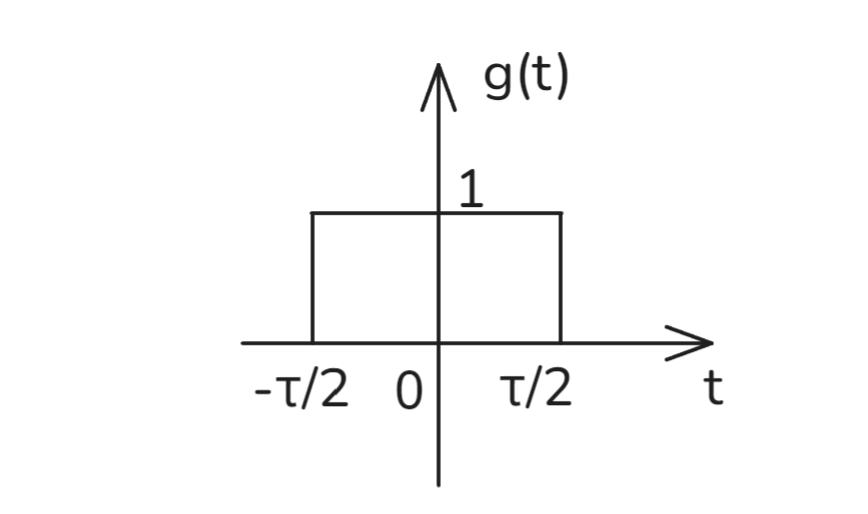
- \(g\to gate\)
与算法竞赛中的差分类似
符号函数\(sgn(t)\)
常用于构造幅度为双极性的信号
单位冲激信号\(\delta(t)\)
矩形脉冲可以视作作用效果(面积)一定,作用时间与作用力大小成反比的力
矩形脉冲持续时间减小,要维持力的效果不变,则需要增大脉冲的幅度
单位冲激信号可以视为作用效果不变,但是作用时间无限小,从而大小无限大的一个力,取脉冲持续时间趋于0,就可以得到单位冲激信号
物理定义:
记宽度为\(\tau\),幅度为1的矩形脉冲门函数为\(g_{\tau}(t)\),则冲激信号的定义为:
狄拉克定义:
在\(t_{0}\)之外的取值全部是0,但是在实数轴上积分为1
广义函数定义:
对于检验函数\(\varphi(t)\),乘以冲激信号后积分,可以将\(t_{0}\)处的\(\varphi\)值抽取出来,即取样
\(\delta(t)\)的性质
- 奇偶性:冲激信号为偶函数
- 与普通函数相乘:
-
\[\begin{cases}f(t)\delta(t)=f(0)\delta(t)\\ \\f(t)\delta(t-t_{0})=f(t_{0})\delta(t-t_{0})\end{cases} \]
-
- 取样性质:
-
\[\begin{align}&\int_{-\infty}^{+\infty} \delta(t)f(t)dt=f(0)\\ \\&\int_{-\infty}^{+\infty} \delta(t-t_{0})f(t)dt=f(t_{0})\end{align} \]
- 相当于将\(f(t)\)的值抽取出来
- 由上一个性质积分而来
-
\[\int_{t_{1}}^{t_{2}}f(t)\delta(t-t_{0})dt=\begin{cases}f(t_{0}),\quad t_{0}\in[t_{1},t_{2}]\\ \\0,\quad t_{0}\not\in[t_{1},t_{2}]\end{cases} \]
-
- 尺度变换性质:
-
\[\delta(at)=\frac{1}{|a|}\delta(t)\ (a\neq 0) \]
-
\[\delta(at-t_{0})=\frac{1}{|a|}\delta\left( t-\frac{t_{0}}{a} \right) \]
-
\[\int_{-\infty}^{+\infty}f(t)\delta(at-t_{0})dt=\frac{1}{|a|}f\left( \frac{t_{0}}{a} \right) \]
-
- \(\delta(t)\)与\(\varepsilon(t)\)的关系:
-
\[\delta(t)=\frac{d}{dt}\varepsilon(t) \]
-
\[\varepsilon(t)=\int_{-\infty}^t\delta(x)dx \]
- 若信号的函数值有跳变,则信号在跳变点处的导数为冲激信号,其冲激强度为信号在跳变点处的跳跃值
-
冲激偶信号\(\delta'(t)\)
冲激偶信号为冲激信号对时间的导数,即$$\delta'(t)=\frac{d}{dt}\delta(t)$$
假如冲激信号由三角形的不断逼近来定义,那么其导数便是奇函数
\(\delta'(t)\)的性质
- 奇偶性:冲激偶信号为奇函数,\(\int_{-\infty}^{+\infty}\delta'(t)dt=0\)
- 与普通函数相乘:
推导:
记忆:\(\left( \frac{\delta(t)}{f(t)} \right)'\)的分子部分
-
取样性质:
-
\[\int_{-\infty}^{+\infty}f(t)\delta'(t)dt=-f'(0) \]
-
\[\int_{-\infty}^{+\infty}f(t)\delta'(t-t_{0})dt=-f'(t_{0}) \]
- 这两个性质由上一条性质积分而来
- 可以将函数的负导数抽取出来
-
-
尺度变换性质:
-
\[\delta'(at)=\frac{1}{a|a|}\delta'(t)=\frac{1}{sgn(a)·a^2}\delta'(t)\ (a\neq 0) \]
- 需要特殊记忆分母的区别!
-
例4
- 注意计算前看看\(t_{0}\)是否在积分区域中
- 注意各个奇异信号之间的转换
基本离散序列
单位序列\(\delta(k)\)
取样性质:
辨析:
- \(\delta(k)\)在\(k=0\)的值为1
- \(\delta(t)\)在\(t=0\)的幅度无穷大
- 一个是离散序列,一个是奇异信号
单位阶跃序列\(\varepsilon(k)\)
\(\varepsilon(k)\)与\(\delta(k)\)的关系:
类比前缀和与差分和的关系
辨析:
- \(\varepsilon(k)\)在\(k=0\)处有定义,值为1
- \(\varepsilon(t)\)在\(t=0\)处无定义或取\(\frac{1}{2}\)
- 一个是离散序列,一个是奇异信号
单边指数序列
根据\(\alpha\)的正负、\(|\alpha|\)与1的大小关系,可以画出四个不同图像
复指数序列
类比复指数信号的讨论,分实部虚部讨论即可得到不同的图像
正弦序列
其中\(\omega_{0}\)称为数字角频率
区别于\(f(t)=\cos \omega t\)中的模拟角频率
正弦序列可以视为正弦信号的采样
设连续正弦信号为\(\cos \Omega_{0}t\),令\(t=kT\)进行采样,则可以得到离散正弦序列\(\cos \Omega_{0}t\bigg|_{t=kt}=\cos \Omega_{0}Tk=\cos \omega_{0}k\)
则有:
数字角频率是一个相对量,单位为\(rad\),可以根据模拟角频率和采样周期确定
正弦序列与虚指数序列的周期性
- 当\(\frac{2\pi}{\omega_{0}}\)为整数时,取\(m=1\),序列为周期序列,周期\(N=\frac{2\pi}{\omega_{0}}\)
- 当\(\frac{2\pi}{\omega_{0}}\)为有理数时,设\(\frac{2\pi}{\omega_{0}}=\frac{P}{Q}\),\(gcd(P,Q)=1\),取\(m=Q\),则序列为周期序列,周期\(N=P\)(等于分子)
- 当\(\frac{2\pi}{\omega_{0}}\)为无理数时,不存在整数\(N\),序列不具备周期性
特别地,两个周期序列之和必定为周期序列,周期的计算方式与连续周期信号之和的周期一样
例5
判断序列是否为周期序列,如果是,求周期
- \(1)f(k)=5\cos4k\)
- \(\omega=4, \frac{2\pi}{\omega}=\frac{\pi}{2}\)为无理数,非周期序列
- \(2)f(k)=\cos \frac{3\pi}{4}k+\cos \frac{2\pi}{3}k\)
- \(N_{1}=8,N_{2}=3,N=lcm(N_{1},N_{2})=24\)
- \(3)f(k)=\cos \frac{\pi}{3k}+e^{j \frac{2\pi}{5}k}\)
- \(N_{1}=5,N_{2}=6,N=lcm(N_{1},N_{2})=30\)
1.3 信号的基本运算
信号的加乘运算
将同一时刻的值相加或相乘即可
信号的平移
左加右减即可
信号的尺度变换
- \(f(t)\to f(at)\)相当于将原信号压缩为\(\frac{1}{a}\)倍
- 尺度变换的时候需要特别处理对冲激信号的尺度变换:\(\delta(at)=\frac{1}{|a|}\delta(t)\)
连续信号的微分与积分
- 连续信号的微分:
- \(f'(t)=\frac{d}{dt}f(t)\)
- 可以体现信号的变化
- 连续信号的积分:
- \(f^{(-1)}(t)=\int_{-\infty}^tf(x)dx\)
- 可以平滑信号的变化
例
- 在微分过程中,可以通过\(\delta(t)\)的取样性质进行化简
- 在积分过程中,需要使用\(\varepsilon(t)\)函数对积分上下界进行刻画!
连续信号的差分与求和
离散序列的差分
- 一阶前向差分:\(\Delta f(k)=f(k+1)-f(k)\)
- 一阶后向差分:\(\nabla f(k)=f(k)-f(k-1)\)
- 其中\(\Delta,\nabla\)为差分算子
- \(\nabla f(k)=\Delta f(k-1)\)
离散序列的求和
1.4 系统的描述与分类
系统的描述
系统的数学模型
-
输入-输出描述法:
- 着眼于系统的输入与输出的关系,适用于单输入-单输出系统
- 连续系统常用微分方程进行表征
- 离散系统常用差分方程进行表征
-
状态变量描述法:
- 既可描述输入输出的关系,又可以描述系统内部的状态,更适合调整系统内部参数,实现最优控制
- 既可以用于单输入-单输出系统,又可以用于多输入-多输出系统
- 用状态方程和输出方程进行表征
系统的框图描述
-
用框图表示输入输出的运算关系,每个框图反映一种数学运算功能,若干个框图可以组成一个完整的系统
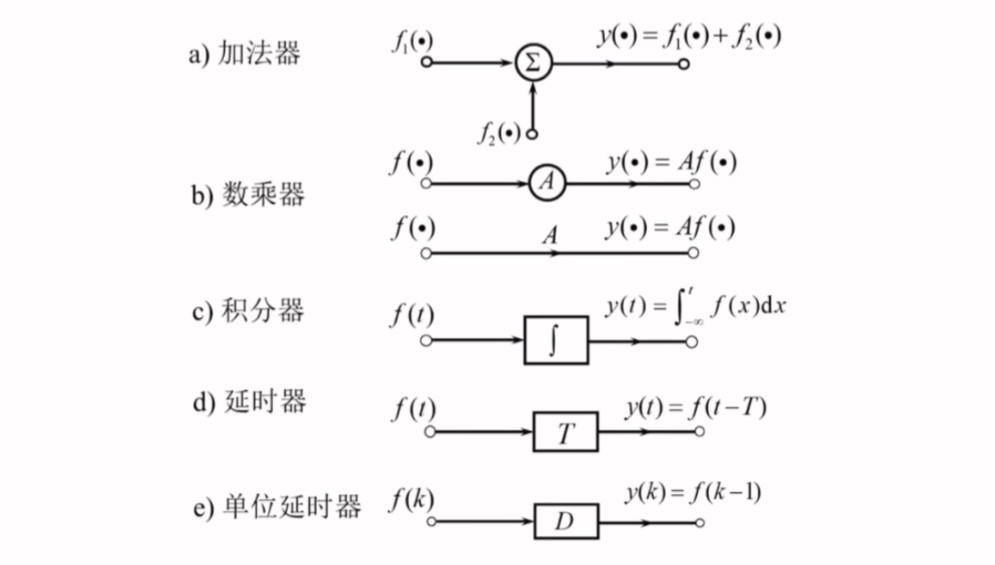
-
注意积分器反向走就是求导
连续系统框图与微分方程

如何看图写出系统微分方程:
- 通过积分器的个数来判断阶数
- 设最后一个积分器得到的结果为\(x(t)\),一路往回得到其导数
- 对左、右加法器列出方程
- 消去\(x(t)\)得到系统微分方程
图中的系统微分方程:
离散系统框图与差分方程
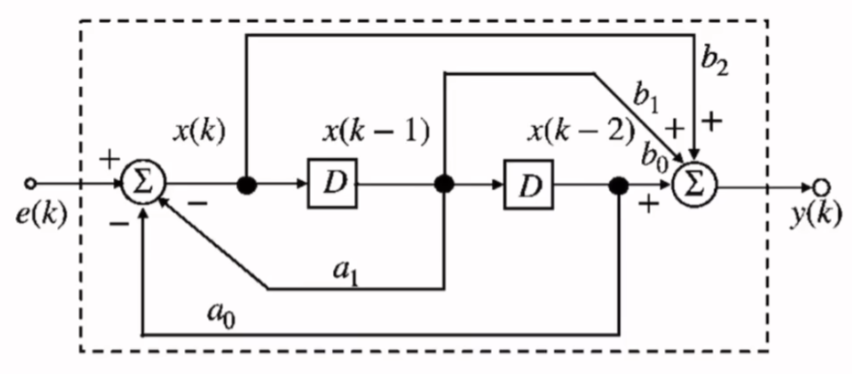
如何看图写出系统差分方程:
- 通过单位延时器的个数判断系统阶数
- 在第一个单位延时器前面设中间变量\(x(k)\)
- 对左右加法器列方程
- 消去中间变量\(x(k)\)
图中的系统差分方程:
系统的分类
连续(时间)系统与离散(时间)系统
- 连续系统:系统输入和输出均为连续时间信号,用微分方程表征
- 离散系统:系统输入和输出均为离散时间信号,用差分方程表征
即时(无记忆)系统与动态(记忆)系统
- 即时系统:系统输出取决于同一时刻的输入,而与历史状态无关,用代数方程表征,如电阻电路
- 动态系统:输出同时取决于同一时刻的输入与系统的历史状态,用微分/差分方程表征,如\(RLC\)动态电路
线性系统与非线性系统
- 线性系统:满足均匀性和叠加性
- 均匀性:系统的激励信号增大\(K\)倍时,系统响应也增大\(K\)倍
- 叠加性:几个激励信号同时作用于系统时,系统响应等于各个激励信号单独作用于系统的响应之和
- \(f(K·x)=K·f(x)\ ,\ f(x+y)=f(x)+f(y)\)
- 非线性系统:与线性系统相对,不具备均匀性或叠加性
时变系统与时不变系统
- 时变系统:系统参数随着时间变化
- 时不变系统:系统参数不随时间变化
因果系统与非因果系统
- 因果系统:当且仅当输入激励时,系统才会出现响应,即响应不会先于激励
- 非因果系统:响应先于激励产生的系统
稳定系统与不稳定系统
- 稳定系统:输入有界,输出也有界的系统
- 不稳定系统:与稳定系统相对
在这门课程中主要学习线性时不变系统
1.5 线性时不变系统的性质
\(LTI-Linear\ Time\ Invariant\ 线性时不变系统\)
\(LSI-Linear\ Shift\ Invariant\ 线性移不变系统\)
线性性质与分解特性
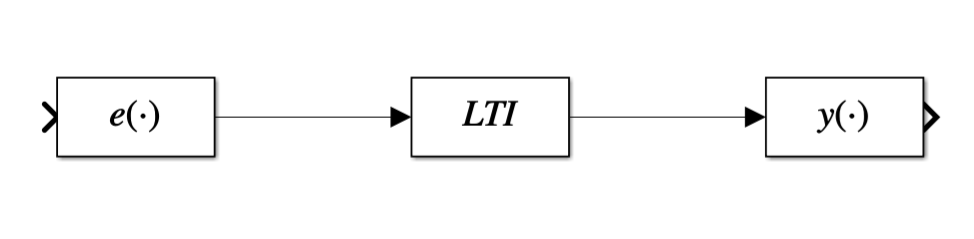
- 其中\(T\)为映射
- 反映了输入-输出关系
线性性质
- 均匀性:系统的激励增大\(K\)倍时,响应也相应增加\(K\)倍
- 叠加性:几个激励信号同时作用于系统时,系统响应等于各个激励信号单独作用于系统的响应之和
如何判断系统的线性性
- 将\(y_{1},y_{2}\)分别用\(e_{1},e_{2}\)表示
- 对\(y(\cdot)=T[e(\cdot)]\)带入\(ae_{1}+be_{2}\),对比结果是否等于\(ay_{1}+by_{2}\)
例
判断下列系统是否是线性系统:
- 注意处理复数的时候,虚数单位\(j\)也可以作为常数来相乘!
分解特性
-
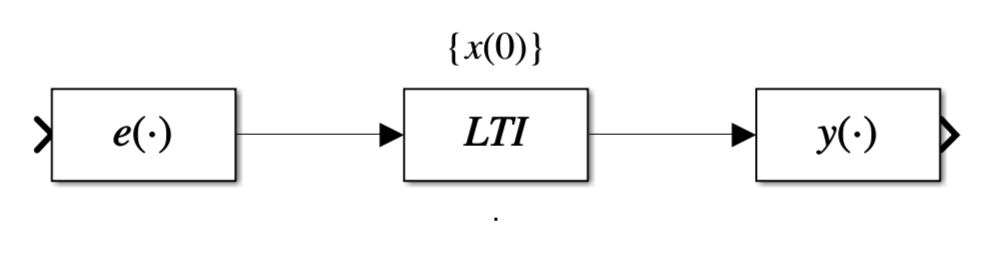
动态系统的响应由激励和初始状态共同决定
-
初始状态集合:\(\{ x(0) \}\)
-
零输入响应:
- \(y_{zi}(\cdot)=T[\{ x(0) \},\{ 0 \}]\)
- \(zi-zero\ input\)
- 激励为0,仅由初始状态引起的系统响应
-
零状态响应:
- \(y_{zs}(\cdot)=T[\{ 0 \},\{ e(\cdot) \}]\)
- \(zs-zero\ state\)
- 初始状态为0,仅由激励引起的系统响应
-
零输入线性
- 零输入响应对系统的初始状态有线性关系:

- 零输入响应对系统的初始状态有线性关系:
- 零状态线性
- 零状态响应对系统的激励有线性关系:
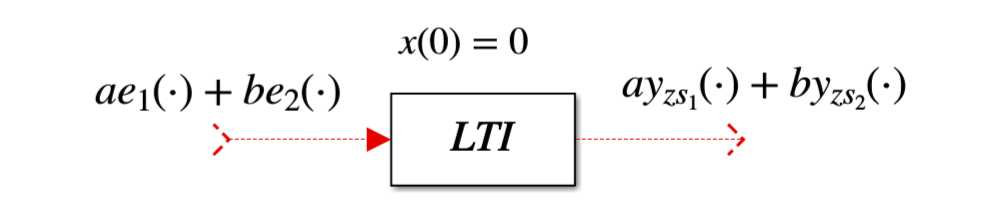
- 零状态响应对系统的激励有线性关系:
如何判断系统是否是线性系统
- 判断是否可以分解为\(y_{zi}(\cdot)+y_{zs}(\cdot)\)
- 若可分解,判断是否满足零输入线性和零状态线性
例
时不变性质
- 时不变系统的响应形式与激励接入系统的时间无关,激励延时,输出也产生相应延时而波形不变
如何判断时不变
-
原理法:
- \(y_{1}(t)=T[e(t-t_{d})]\)
- 比较\(y(t-t_{d})\)与\(y_{1}(t)\)即可
-
直观法:
- 若信号之前出现变系数\(f(t)\cdot e(t)\),或者信号有反转或尺度变换\(e(at+b)\),则系统为时变系统
-
需要特别注意的是:
- 如\(y(t)=e(2t)\),\(y_{1}(t)=T[e(t-t_{d})]=e(2t-t_{d})\)
- 对\(e(t-t_{d})\)时域压缩后为\(e(2t-t_{d})\)
- \(y(t-t_{d})=e(2t-2t_{d})\neq y_{1}(t)\),所以是时变系统
例
1):
某\(LTI\)连续系统,输入为\(e_{1}(t)\)时,零状态响应为\(y_{sz_{1}}(t)\),当输入为\(e_{2}(t)\)时,求该系统的零状态响应\(y_{zs_{2}}(t)\)
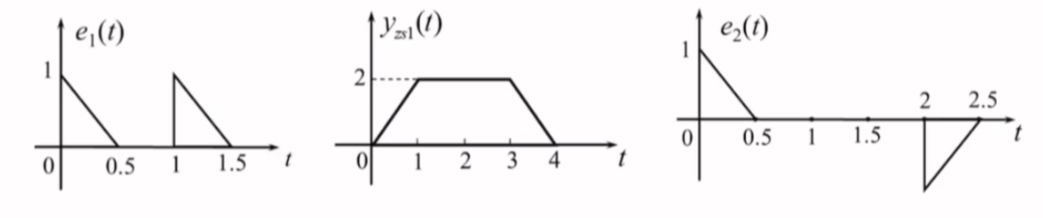
- 观察可知\(e_{2}(t)=e_{1}(t)-e_{1}(t-1)\)
- 由零状态线性可知:\(y_{zs_{2}}(t)=y_{zs_{1}}(t)-y_{zs_{1}}(t-1)\)
- 画图即可
2):
已知\(LTI\)系统:
求\(y_{3}(t)=T[\{ 2x(0) \},\{ 5e(t) \}]\)和\(y_{4}(t)=T[\{ 2x(0) \},\{ 5e(t-2) \}]\):
微分与积分性质(零状态)
- 激励求导或积分,响应为原响应求导或积分
- 该性质对于高阶导数或重积分同样适用
因果性与稳定性
因果性
- 若系统为因果系统,则零状态响应只能在激励产生的瞬间或者之后再出现
- \(t=t_{0}\ (k=k_{0})\)时系统响应 只与\(t\leq t_{0}\ (k\leq k_{0})\)时的激励有关
- 因果信号:\(e(\cdot)=0,t<0或k<0\)
- 因果系统中,激励为因果信号,响应也一定是因果信号
- \(y(t)=e(2t)\)为非因果系统
- \(y(t)=e(t)\sin(t+1)\)是因果系统(只与激励有关)
稳定性
稳定系统满足:
- 若系统对有界输入的零状态响应也有界,则系统为稳定系统
- 注意是\(|e(x)|<\infty\),而\(t\to \infty,k\to \infty\)是可以的
- \(y_{zs}(k)=(k-2)e(k)\),若\(\lim_{ k \to \infty }e(k)=A\),则\(\lim_{ k \to \infty }(k-2)e(k)=\infty\),不是稳定系统


 浙公网安备 33010602011771号
浙公网安备 33010602011771号