并查集基本概念

问题描述

---

所谓并查集，顾名思义就是在一堆集合进行合并的同时进行查询。再具体一点：假设有N个元素，每个元素各自构成一个集合，现在我们不断地随便在其中抽取两个集合并使它们合并，在抽取集合并合并的过程中，再随机抽两个元素，询问你这两个元素是否来自于同一个集合。

解题思路

---

基本方法

问题的关键点在于：怎么找到一个通用且快速的方法，使得我们能在各个集合动态合并的过程中正确判断出某个元素在哪个集合。想象一下若你和你最好的朋友一起升入同一所高中，你想知道你和你的朋友是否被分在了同一个班。你会去按着花名册一个个去找自己的名字和朋友的名字吗？当然不会，你会直接问问看你的朋友是哪班的，根据朋友的回答，你就能快速的得到答案。

并查集的解决方案类似于这种思想，在不考虑路径压缩的情况下，我们可以把一个集合想象为一棵树。这棵树上的所有节点对应着集合上的所有元素，任意一节点向祖先溯源必定能到达根节点，而这棵树的根节点的祖先就是它自己。

很明显，树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

若想求任意两个子节点是否来自同一颗树，一个很朴素的解决方法是让这两个点一直找自己的祖先节点，直到找到树根，若两者根节点相同，那明显它们来自同一棵树，来自同一个集合。

有了思路问题就好解决了。
关键三步：
1、一开始令所有元素自身构成一个单一元素的集合。在没合并前，每个元素都是一棵树，互不相关。
请务必注意这句注释：元素用数组下标表示，数组内的值为下标的父节点

int pre[20000];//注意，此时元素用数组下标表示，数组内的值为下标的父节点
                       //如pre[6]=3;说明元素6的直接父节点为3
for(int i=0;i<2000;i++)
	pre[i]=i;

2、若要确定某节点来自于哪个集合，就一直去找它的父节点，直到找到根。（节点的根节点标识了唯一一个集合）

int topsearch(int node)//通常也命名为Find()函数
{
	while(pre[node]!=node)
		node=pre[node];
	return node;
} 

3、假设要让X、Y两棵树进行合并，那就把Y树连根拔起，整个嫁接到X上，这下，Y上任意一个点的根节点都是X的根节点，X树，Y树同根同源，自然就成为了一个集合。

void join(int node1,int node2) //两个节点，把他们变成朋友，通常也命名为Union()函数
{
	int x=topsearch(node1);//找node1的老大x 
	int y=topsearch(node2);//找node2的老大y 
	if(x!=y)
	{
		pre[y]=x;//让x变成y的老大，现在node1和node2的老大都是x了 
	}
} 

优化

---

我们注意到，若要找出某个节点的根节点，可能要经过很多祖先节点。

那为什么不让所有节点的父节点都为根节点呢？这样子每个节点只用走一步就能确定根节点了（根节点的父节点为自己），大大缩短了搜索路径。

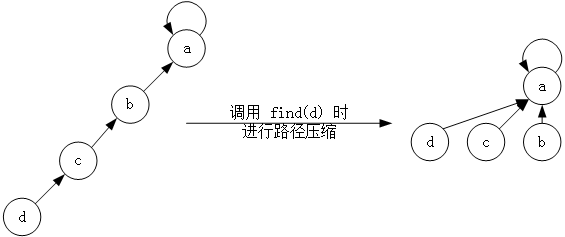
这就是所谓的路径压缩。路径压缩可以在搜索时顺便完成，也可以在合并时一直保持最短路径。写法很多，很自由。

int topsearch(int node)//通常也命名为Find()函数
{
    int son,temp;
	while(pre[node]!=node)
		node=pre[node];
    while(son!=node)//路径压缩
    {
        temp=pre[son];
        pre[son]=node;
        son=temp;
    }
	return node;
} 

整体代码

---

//洛谷并查集简单题
//清楚思路写法
#include <iostream>
using namespace std;
int pre[20001];
int topsearch(int node)
{
    int son,temp;
	while(pre[node]!=node)
		node=pre[node];
    while(son!=node)//路径压缩
    {
        temp=pre[son];
        pre[son]=node;
        son=temp;
    }
	return node;
} 
void join(int node1,int node2) //两个节点，把他们变成朋友 
{
	int x=topsearch(node1);//找node1的老大x 
	int y=topsearch(node2);//找node2的老大y 
	if(x!=y)
	{
		pre[y]=x;//让x变成y的老大，现在node1和node2的老大都是x了 
		//pre[node2]=x;//也是一种路径压缩
	}
} 
int main() 
{
	int m,n;
	cin>>n>>m;
	for(int i=0;i<=n;i++)
		pre[i]=i;
	while(m--)
	{
		int x,y,z;
		cin>>z>>x>>y;
		if(z==1)
			join(pre[x],pre[y]);
		else
		{
			if(topsearch(x)!=topsearch(y))
				cout<<"N"<<endl;
			else
				cout<<"Y"<<endl;
		}
	}
}

//精简写法（注意递归的使用）
#include<bits/stdc++.h>
using namespace std;
int pre[20001],m,n;
int find(int node){
	if(pre[node]==node) 
		return node;
	else
		return pre[node]=find(pre[node]);//递归同时路径压缩
} 
int main() {
	cin>>n>>m;
	for(int i=0;i<=n;i++) 
		pre[i]=i;
	while(m--){
		int x,y,z;
		cin>>z>>x>>y;
		if(z==1)
			pre[find(y)]=find(x);
		else{
			if(find(x)!=find(y))
				cout<<"N"<<endl;
			else
				cout<<"Y"<<endl;
		}
	}
}

其他

---

友情参考链接：
https://www.cnblogs.com/wkfvawl/p/9063836.html
https://blog.csdn.net/qq_41593380/article/details/81146850

更新日志：
2020/4/16 初次创立
2020/4/27 调整语序，对集合树做出了更详细的描述