深度人脸识别综述

目录

• Introduction
• Euclidean Based Metric Learning
  • Contrastive loss
  • Triplet Loss
  • Center Loss
  • Center-Invariant Loss
  • Range Loss
  • Summary
• Margin Based Classification
  • Softmax Loss
  • L-Softmax Loss
  • A-Softmax Loss
  • NormFace
  • AM-Softmax Loss
  • CosFace
  • ArcFace
  • Summary
• References
  • Overview
  • Blogs

---

Introduction

人脸识别系统通常由以下构建模块组成：

• 人脸检测。人脸检测器用于寻找图像中人脸的位置，如果有人脸，就返回包含每张人脸的边界框的坐标。如图 3a 所示。
• 人脸对齐。人脸对齐的目标是使用一组位于图像中固定位置的参考点来缩放和裁剪人脸图像。这个过程通常需要使用一个特征点检测器来寻找一组人脸特征点，在简单的 2D 对齐情况中，即为寻找最适合参考点的最佳仿射变换。图 3b 和 3c 展示了两张使用了同一组参考点对齐后的人脸图像。更复杂的 3D 对齐算法（如 [16]）还能实现人脸正面化，即将人脸的姿势调整到正面向前。
• 人脸表征。在人脸表征阶段，人脸图像的像素值会被转换成紧凑且可判别的特征向量，这也被称为模板（template）。理想情况下，同一个主体的所有人脸都应该映射到相似的特征向量。
• 人脸匹配。在人脸匹配构建模块中，两个模板会进行比较，从而得到一个相似度分数，该分数给出了两者属于同一个主体的可能性。

人脸识别相关方法的发展如下图所示：

---

对于基于 CNN 的人脸识别方法，影响准确度的因素主要有三个：训练数据、CNN 架构和损失函数。

因为在大多数深度学习应用中，都需要大训练集来防止过拟合。一般而言，为分类任务训练的 CNN 的准确度会随每类的样本数量的增长而提升。这是因为当类内差异更多时，CNN 模型能够学习到更稳健的特征。但是，对于人脸识别，我们感兴趣的是提取出能够泛化到训练集中未曾出现过的主体上的特征。因此，用于人脸识别的数据集还需要包含大量主体，这样模型也能学习到更多类间差异。

人脸识别实验中常用到close-set和open-set：

• close-set：就是所有的测试集都在训练集中出现过。所以预测结果是图片的ID，如果想要测试两张图片是否是同一个，那么就看这两张图片的预测ID是否一样即可。
• open-set：就是测试的图片并没有在训练集中出现过，那么每张测试图片的预测结果是特征向量，如果想要比较两张图片的人脸是否属于同一个人，需要测试图像特征向量的距离。

---

在光照较差，遮挡，形变（大笑），侧脸等诸多条件下，神经网络很难提取出与“标准脸”相似的特征，异常脸在特征空间里落到错误的位置，导致识别和验证失败。这是现代人脸识别系统的局限，一定程度上也是深度学习（深度神经网络）的局限。

面对这种局限，通常采取三种应对措施，使人脸识别系统能正常运作：

1. 工程角度：研发质量模型，对检测到人脸质量进行评价，质量较差则不识别/检验。

2. 应用角度：施加场景限制，比如刷脸解锁，人脸闸机，会场签到时，都要求用户在良好的光照条件下正对摄像头，以避免采集到质量差的图片。

3. 算法角度：提升人脸识别模型性能，在训练数据里添加更多复杂场景和质量的照片，以增强模型的抗干扰能力。

---

Euclidean Based Metric Learning

Contrastive loss

DeepID1并不属于contrastive loss系列，只是作为DeepID系列的开山之作而放在这里。

DeepID1:《Deep Learning Face Representation from Predicting 10,000 Classes》

DeepID2:《Deep learning face representation by joint identification-verification》

DeepID2+:《Deeply learned face representations are sparse, selective, and robust》

DeepID3:《Deepid3: Face recognition with very deep neural networks》

\[\operatorname{Ident}\left(f, t, \theta_{i d}\right)=-\sum_{i=1}^{n} p_{i} \log \hat{p}_{i}=-\log \hat{p}_{t} \]

\[\operatorname{Verif}\left(f_{i}, f_{j}, y_{i j}, \theta_{v e}\right)=\left\{\begin{array}{ll}{\frac{1}{2}\left\|f_{i}-f_{j}\right\|_{2}^{2}} & {\text { if } y_{i j}=1} \\ {\frac{1}{2} \max \left(0, m-\left\|f_{i}-f_{j}\right\|_{2}\right)^{2}} & {\text { if } y_{i j}=-1}\end{array}\right. \]

DeepID1:

DeepID2:

DeepID2+:

DeepID3:

---

Triplet Loss

《Facenet: A unified embedding for face recognition and clustering》

\[\sum_{i}^{N}\left[\left\|f\left(x_{i}^{a}\right)-f\left(x_{i}^{p}\right)\right\|_{2}^{2}-\left\|f\left(x_{i}^{a}\right)-f\left(x_{i}^{n}\right)\right\|_{2}^{2}+\alpha\right] \]

---

Center Loss

《A Discriminative Feature Learning Approach for Deep Face Recognition》

\[\begin{aligned} \mathcal{L} &=\mathcal{L}_{S}+\lambda \mathcal{L}_{C} \\ &=-\sum_{i=1}^{m} \log \frac{e^{W_{y_{i}}^{T} \boldsymbol{x}_{i}+b_{y_{i}}}}{\sum_{j=1}^{n} e^{W_{j}^{T} \boldsymbol{x}_{i}+b_{j}}}+\frac{\lambda}{2} \sum_{i=1}^{m}\left\|\boldsymbol{x}_{i}-\boldsymbol{c}_{y_{i}}\right\|_{2}^{2} \end{aligned} \]

\(c_{y_i}\)代表样本\(i\)对应类别\(y_i\)所属的类中心。理想情况下，这个类中心在每次迭代时都需要利用整个数据集的特征来更新，但是这会需要巨大的计算量。因此，在实际使用中，做了如下修改：

• 由整个训练集更新center改为mini-batch更新center；
• 避免错误分类的样本的干扰，使用scalar α 来控制center的学习率；

虽然center loss取得了良好的结果，但是也有一些不足之处。Center Loss考虑到了使得类内紧凑，却不能使类间可分；另外训练样本对的选择也较为麻烦。在论文中，作者也提到了，选取合适的样本对对于模型的性能至关重要，论文中采用的方法是每次选择比较难以分类的样本对重新训练，类似于hard-mining。同时，合适的训练样本还可以加快收敛速度。

---

Center-Invariant Loss

《Deep face recognition with center invariant loss》

\[\begin{aligned} L=& L_{s}+\gamma L_{I}+\lambda L_{c} \\=&-\log \left(\frac{e^{\mathbf{w}_{y}^{T} \mathbf{x}_{i}+b_{y}}}{\sum_{j=1}^{m} e^{\mathbf{w}_{j}^{T} \mathbf{x}_{i}+b_{j}}}\right)+\frac{\gamma}{4}\left(\left\|\mathbf{c}_{y}\right\|_{2}^{2}-\frac{1}{m} \sum_{k=1}^{m}\left\|\mathbf{c}_{k}\right\|_{2}^{2}\right)^{2} \\ &+\frac{\lambda}{2}\left\|\mathbf{x}_{i}-\mathbf{c}_{y}\right\|^{2} \end{aligned} \]

---

Range Loss

《Range loss for deep face recognition with long-tail》

\[\mathcal{L}_{R}=\alpha \mathcal{L}_{R_{i n t r a}}+\beta \mathcal{L}_{R_{i n t e r}} \]

\[\mathcal{L}_{R_{i n t r a}}=\sum_{i \subseteq I} \mathcal{L}_{R_{i n t r a}}^{i}=\sum_{i \subseteq I} \frac{k}{\sum_{j=1}^{k} \frac{1}{\mathcal{D}_{j}}} \]

\[\begin{aligned} \mathcal{L}_{R_{\text { inter }}} &=\max \left(m-\mathcal{D}_{\text {Center}}, 0\right) \\ &=\max \left(m-\left\|\overline{x}_{Q}-\overline{x}_{\mathcal{R}}\right\|_{2}^{2}, 0\right) \end{aligned} \]

\[\mathcal{L}=\mathcal{L}_{M}+\lambda \mathcal{L}_{R}=-\sum_{i=1}^{M} \log \frac{e^{W_{y_{i}}^{T} x_{i}+b_{v_{i}}}}{\sum_{j=1}^{n} e^{W_{j}^{T} x_{i}+b_{j}}}+\lambda \mathcal{L}_{R} \]

---

Summary

基于欧式距离的Metric Learning符合人的认知规律，在实际应用中也取得了不错的效果，但是它有非常致命的两个问题：

• 模型需要很长时间才能拟合，contrastive loss和triplet loss的训练样本都基于pair或者triplet的，可能的样本数是O(N2)或者O(N3)的。当训练集很大时，基本不可能遍历到所有可能的样本，所以一般来说需要很长时间才能拟合；
• 模型好坏很依赖训练数据的sample方式，理想的sample方式不仅能提升算法最后的性能，更能略微加快训练速度。

Margin Based Classification

Softmax Loss

\[L=\frac{1}{N} \sum_{i} L_{i}=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{f_{y_{i}}}}{\sum_{j} e^{f_{j}}}\right) \]

\[L_{i}=-\log \left(\frac{e^{\left\|\mathbf{W}_{y_{i}}\right\|\left\|\mathbf{x}_{i}\right\| \cos \left(\theta_{y_{i}}\right)}}{\sum_{j} e^{\left\|\mathbf{W}_{j}\right\|\left\|\mathbf{x}_{\mathbf{i}}\right\| \cos \left(\theta_{j}\right)})}\right) \]

这里的W可以理解为一组基向量，每一个维度对应一个类别。\(W_iX_i\)即将数据\(X_i\)映射到类别\(i\)对应的维度上，\(X_i\)与基向量\(W_i\)的夹角越小，则数据\(X_i\)属于类别\(i\)的概率越大。因此，对于一个二分类问题而言，只要\(X_i\)与其中一个基向量\(W_i\)的夹角小于45°，则\(X_i\)即被分类为类别\(i\)。

从上述分析可以看出，基于Softmax的分类只要求能够得到正确的分类结果，但是这种形式并不能够有效地学习得到使得类内较为紧凑、类间较离散的特征。

---

L-Softmax Loss

《Large-margin softmax loss for convolutional neural networks》

\[L_{i}=-\log \left(\frac{e^{\left\|\mathbf{W}_{y_{i}}\right\|\left\|\mathbf{x}_{i}\right\| \psi\left(\theta_{y_{i}}\right)}}{\left\|\mathbf{W}_{y_{i}}\right\|\left\|\mathbf{x}_{i}\right\| \psi\left(\theta_{y_{i}}\right)+\sum_{j \neq y_{i}} e^{\left\|\mathbf{W}_{j}\right\|\left\|\mathbf{x}_{i}\right\| \cos \left(\theta_{j}\right)})}\right) \]

其中，\(\psi(\theta)\)可以表示为：

\[\psi(\theta)=\left\{\begin{array}{l}{\cos (m \theta), 0 \leq \theta \leq \frac{\pi}{m}} \\ {\mathcal{D}(\theta), \frac{\pi}{m}<\theta \leq \pi}\end{array}\right. \]

公式中的\(\mathcal{D}(\theta)\)必须是一个单调减函数，且\(\mathcal{D}\left(\frac{\pi}{m}\right)=\cos \left(\frac{\pi}{m}\right)\)， 以保证 \(\psi(\theta)\)是一个连续函数。

为了简化前向和后向传播的计算，作者构建了一种等价的函数形式 \(\psi(\theta)\)：

\[\psi(\theta)=(-1)^{k} \cos (m \theta)-2 k, \theta \in\left[\frac{k \pi}{m}, \frac{(k+1) \pi}{m}\right] \]

Large-Margin Softmax Loss是Softmax Loss引入margin思想的改进版本。即要是数据\(X_i\)不仅能够正确分类，而且与正确类别对应基向量的夹角要大于不同类别基向量的夹角一定的margin角度。因此在学习同类样本时，增强了同类学习的难度，这个难度要比不同类的难度要大些。这样的区别对待使得特征的可区分性增强。

为了简单明了地表明L-Softmax Loss的有效性，作者讨论了一个二分类问题，只包含\(W_1\)和\(W_2\)。分析结果如下图所示：

---

A-Softmax Loss

《Sphereface: Deep hypersphere embedding for face recognition》

\[L_{a n g}=\frac{1}{N} \sum_{i}-\log \left(\frac{\exp \left(\left\|x_{i}\right\| \psi\left(\theta_{y i, i}\right)\right)}{\exp \left(\left\|x_{i}\right\| \psi\left(\theta_{y i}, i\right)\right)+\sum_{j \neq y_{i}} \exp \left(\left\|x_{i}\right\| \cos \left(\theta_{j, i}\right)\right)}\right) \]

A-Softmax与L-Softmax的最大区别在于A-Softmax的权重归一化了，而L-Softmax则没有。A-Softmax权重的归一化导致特征上的点映射到单位超球面上，而L-Softmax则不没有这个限制，这个特性使得两者在几何的解释上是不一样的。如图1所示，如果在训练时两个类别的特征输入在同一个区域时，如下图10所示。A-Softmax只能从角度上分度这两个类别，也就是说它仅从方向上区分类，分类的结果如图2所示；而L-Softmax，不仅可以从角度上区别两个类，还能从权重的模（长度）上区别这两个类，分类的结果如图3所示。在数据集合大小固定的条件下，L-Softmax能有两个方法分类，训练可能没有使得它在角度与长度方向都分离，导致它的精确可能不如A-Softmax。

问题：

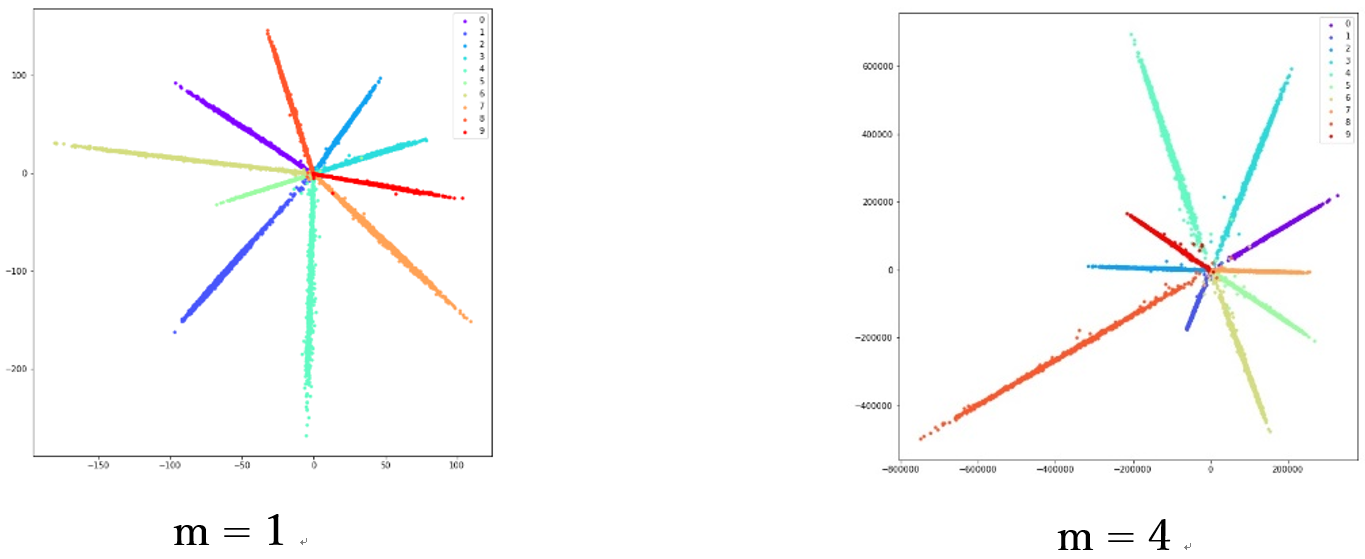
A-Softmax虽然效果很好，但是存在着显著的问题。在测试阶段，A-Softmax通过特征间的余弦值来衡量相似性，即以角度为相似性的度量；但在训练阶段，A-Softmax并不是直接优化特征与类中心的角度，而是优化特征与类中心的角度再乘上一个特征的长度。因此，优化的方向还有一部分是去增大特征的长度。下图是A-Softmax在Mnist数据集上的实验，分别对应m=1和m=4时的特征可视化。注意坐标的尺度，就能验证上述观点。

---

NormFace

NormFace: \(L_2\) Hypersphere Embedding for Face Verification Feng

\[\mathcal{L}_{\mathcal{S},}=-\frac{1}{m} \sum_{i=1}^{m} \log \frac{e^{s \tilde{W}_{y_{i}}^{T} \tilde{\mathrm{f}}_{i}}}{\sum_{j=1}^{n} e^{s \tilde{W}_{j}^{T} \tilde{\mathrm{f}}_{i}}} \]

---

AM-Softmax Loss

《Additive Margin Softmax for Face Verification 》

\[L_{A M S}=-\frac{1}{n} \sum_{i=1}^{n} \log \frac{e^{s \cdot\left(\cos \theta_{y_{i}}-m\right)}}{e^{s\left(\cos \theta_{y_{i}}-m\right)}+\sum_{j=1, j \neq y_{i}}^{c} e^{s \cdot \cos \left(\theta_{j}\right)}} \]

AM-Softmax令\(||x||=1, ||W||=1, b=0\)。\(s\)为缩放因子，论文里固定为30。

角度距离和与余弦距离：

A-Softmax中为\(\cos m\theta_{y_{i}}\)，而AM-Softmax为\(\cos\theta_{y_{i}}-m\)。一个是角度距离（angular margin），一个是余弦距离（cosine margin）。当使用传统的softmax作为损失函数时，角度距离和余弦距离是等价的，即：\(\cos \left(\theta_{1}\right)=\cos \left(\theta_{2}\right) \Rightarrow \theta_{1}=\theta_{2}\)。但当试图改变决策边界时，角度距离和余弦距离便不再等价。最终的决策边界是和余弦相关的，根据cos的性质，优化角度距离比优化余弦距离更有效果，因为余弦距离相对更密集。（为什么论文采用优化余弦距离？）

AM-Softmax的好处在于A-Softmax的倍角计算是要通过倍角公式，反向传播时不方便求导，而只减m反向传播时导数不用变化。

特征归一化：

高质量的图片提取出来的特征范数大，低质量的图片提取出来的特征范数小，如图：

Softmax的目标是尽可能最大化正确分类的概率。它会忽略掉一些比较难分辨的图片（低质量的图片），优先拟合高质量的图片。而L2-Softmax中提到，质量较差的人脸图片的特征范数越小。在进行了特征归一化后，这些质量较差的图片特征会产生更大的梯度，导致网络在训练过程中将更多的注意力集中在这些样本上。因此，对于数据集图片质量较差时，更适合采用特征归一化。

如下图所示，对一个具有二维的特征，正则化后，特征被表示在一个圆中。传统softmax的决策边界即是向量\(P_0\)，则有\(W_{1}^{T} P_{0}=W_{2}^{T} P_{0}\)；而AM-softmax是以决策区域替代决策边界，对于类别1的边界为向量\(P_1\)，定义\(W_{1}^{T} P_{1}-m=W_{2}^{T} P_{1}\)，那么\(m=\left(W_{1}-W_{2}\right)^{T} P_{1}=\cos \left(\theta_{W_{1}}, P_{1}\right)-\cos \left(\theta_{W_{2}}, P_{1}\right)\)。更进一步假设所有的类别都具有相同的方差，\(P_2\)是类别2的边界向量，那么\(\cos \left(\theta_{W_{2}}, P_{1}\right)=\cos \left(\theta_{W_{1}}, P_{2}\right)\)，所以\(m=\cos \left(\theta_{W_{1}}, P_{1}\right)-\cos \left(\theta_{W_{1}}, P_{2}\right)\)。

---

CosFace

CosFace: Large Margin Cosine Loss for Deep Face Recognition

\[L_{l m c}=\frac{1}{N} \sum_{i}-\log \frac{e^{s\left(\cos \left(\theta_{y_{i}, i}\right)-m\right)}}{e^{s\left(\cos \left(\theta_{y_{i}, i}\right)-m\right)}+\sum_{j \neq y_{i}} e^{s \cos \left(\theta_{j, i}\right)}} \]

subject to：

\[\begin{aligned} W &=\frac{W^{*}}{\left\|W^{*}\right\|} \\ x &=\frac{x^{*}}{\left\|x^{*}\right\|} \\ \cos \left(\theta_{j}, i\right) &=W_{j}^{T} x_{i} \end{aligned} \]

---

ArcFace

ArcFace: Additive Angular Margin Loss for Deep Face Recognition

\[L_{3}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}} \]

\(\\cos \left(\theta_{y_{i}}+m\right)\)相当于原始的余弦函数在x轴上向左偏移。论文中将余弦余量\(m\)设置为 0.35(AM-Softmax, CosFace)。与 SphereFace 相比，附加余弦余量（CosineFace）有三个优点：

• 非常容易实现，没有棘手的超参数;
• 没有Softmax监督，更清晰，更易收敛;
• 性能有明显改善。

---

Summary

L-Softmax（\(\cos m\theta_{y_{i}}\)）、A-Softmax（\(\cos m\theta_{y_{i}}\)）、AM-Softmax（\(\cos\theta_{y_{i}}-m\)）、CosFace（\(\cos\theta_{y_{i}}-m\)）、ArcFace（\(\\cos \left(\theta_{y_{i}}+m\right)\)）的本质都是对cosine函数以及margin形式进行改进。区别在于不同的函数形式在前向传播和反向传播时所需的计算量有所不同。

cosine函数的图像为：

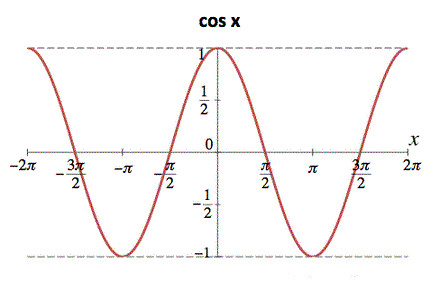
但是上述所有损失函数严格要求每个类别都有相同的margin，没有考虑到类别间的语义相关性，使得训练的难度较大。语义相关性即：部分类别的相似程度高于其他类别，如：猫和狗的相似度高于猫和猴子的相似度。在人脸识别任务中，虽然所有的类别都是人，但是世界上存在着不同的人种：肤色、五官等都有着显著的区别，且不同地区的长相也趋向于不同。而上述损失函数均没有考虑到人种间的差异性和相似性。

---

References

Overview

• 人脸识别技术全面总结：从传统方法到深度学习
• 深度学习人脸识别综述
• 深度人脸识别综述
• 人脸识别的LOSS（上）
• 人脸识别的LOSS（下）

Blogs

• DeepID1,DeepID2
• DeepID人脸识别算法之三代
• 深度学习干货学习—center loss
• 人脸识别系列（六）：FaceNet
• 【论文笔记】Large-Margin Softmax Loss for Convolutional Neural Networks
• A-Softmax的总结及与L-Softmax的对比—SphereFace
• 人脸识别：NormFace
• 人脸识别之AM-Softmax
• ArcFace算法笔记
• 论文阅读之Arcface