矩阵乘法链

1、问题

2、解析 

 

 

 

 

 

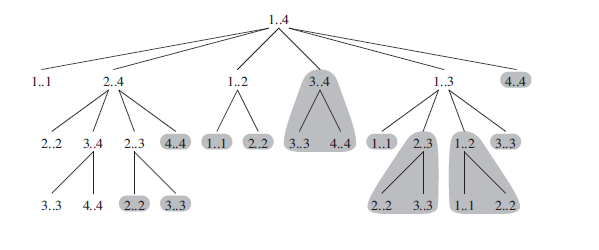
例如P=<20,15,40,35,10,30>,n=5

A1:20*15

A2:15*40

A3:40*35

A4:35*10

A5:10*30

(1)r=1

m[1,1]=0;

m[2,2]=0;

m[3,3]=0;

m[4,4]=0;

m[5,5]=0;

(2)r=2，i=1,2,3,4; j=2,3,4,5

m[1,2]=20*15*40=12000;

m[2,3]=15*40*35=21000;

m[3,4]=40*35*10=14000;

m[4,5]=35*10*30=10500;

　　(3)r=3，i=1,2,3; j=3,4,5

　　m[1,3]=min{ m[1,2]+ m[3,3]+(A1A2)A3, m[1,1]+ m[2,3]+A1(A2A3)}; s[1,3]=1

　　m[2,4]=min{ m[2,3]+ m[4,4]+(A2A3)A4, m[2,2]+ m[3,4]+A2(A3A4)}; s[2,4]=2

　　m[3,5]=min{ m[3,4]+ m[5,5]+(A3A4)A5, m[3,3]+ m[4,5]+A3(A4A5)}; s[3,5]=4

(4)r=4, i=1,2; j=4,5

m[1,4]=min{ m[1,1]+ m[2,4]+A1(A2A3A4), m[1,2]+ m[3,4]+(A1A2)(A3A4),m[1,3]+ m[4,4]+(A1A2A3)A4};

s[1,4]=1

m[2,5]=min{ m[2,2]+ m[3,5]+A2(A3A4A5), m[2,3]+ m[4,5]+(A2A3)(A4A5),m[2,4]+ m[5,5]+(A2A3A4)A5};

s[2,5]=4

(5)r=5,i=1; j=5

m[1,5]=min{ m[1,1]+ m[2,5]+A1(A2A3A4A5),m[1,2]+ m[3,5]+(A1A2)( A3A4A5),m[1,3]+ m[4,5]+ (A1A2A3)(A4A5);m[1,4]+ m[5,5]+ (A1A2A3A4)A5};s[1,5]=4 

　　当n=5时最优解为:29000

　　括号方案为：(A1(A2(A3A4)))A5

3、设计

int n,p[N];
int m[N][N], s[N][N];
void MatrixChainOrder(int* p, int Length){
    n <- Length - 1
    for i <- 1 to n
         m[i][i] = 0
    for l <- 2 to n  /* 枚举矩阵链的长度 */
        for i <- 1 to n - l + 1 /* 枚举起点 */
            j <- i + l - 1         
            m[i][j] <- INT_MAX  /*m[i][j]赋值为无穷大 */
            for k <- i to j - 1 /* 枚举分割点 */
                q <- m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j]
                if q < m[i][j]/*如果当前值更小，修改答案，并记录下分割点 */
                    m[i][j] <- q
                    s[i][j] <- k
}

4、分析

动态规划求解需要三重循环：

第一重枚举链长度，第二重枚举起点，第三重枚举分割点。

所以时间复杂度O(n)=n^3。

5、源码

https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/MatrixChainOrder.cpp