最短路(Floyd+Dijkstra)

Floyd算法

1、问题

　　在无向图 G=(V,E) 中，(u,v)代表连接点u与顶点v的边，而w(u,v)代表此边的权重，求所有顶点之间的最短距离。

2、解析

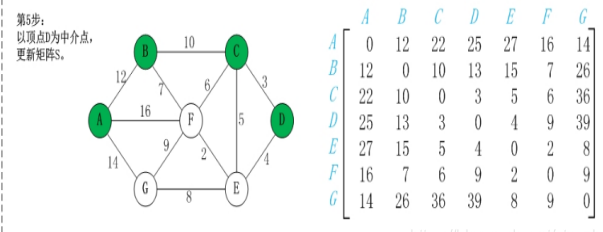
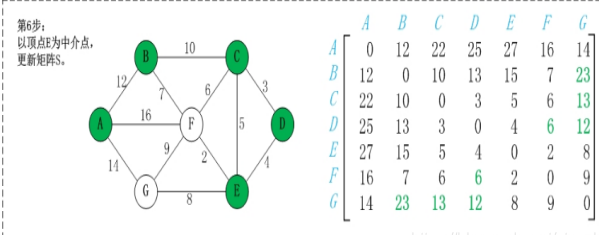
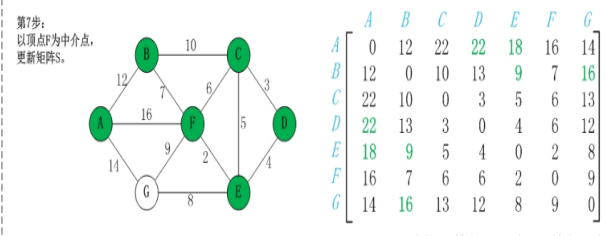
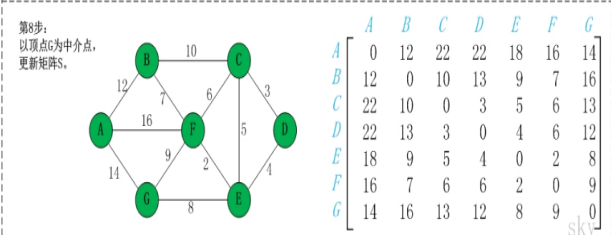
步骤一：选定一个未选择过的点为中间节点(一般从1-n顺序选取)

步骤二：遍历整个矩阵，查看是否可以通过该点修改两点之间的最短距离

步骤三：重复步骤二直到所有点均被选择

  

  

  

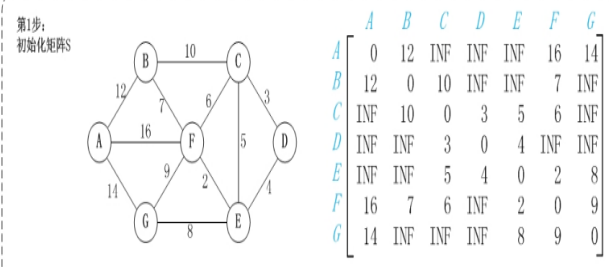
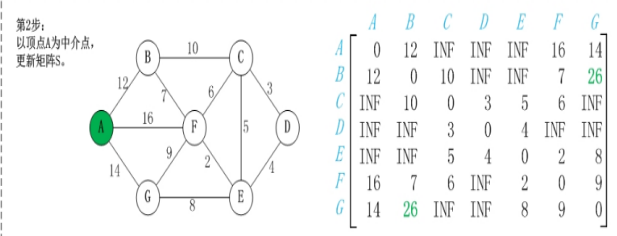
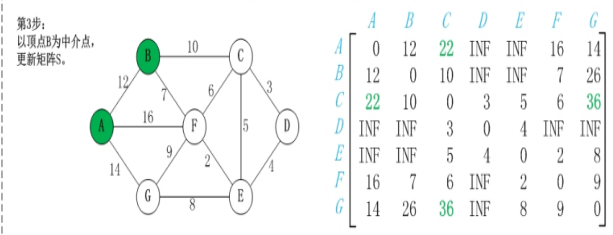
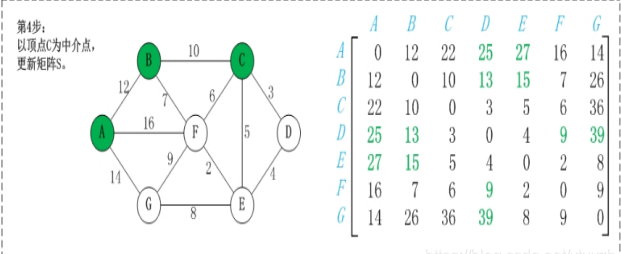
3、设计

1 for k <- 1 to n
2     for i <- 1 to n
3         for j <- 1 to n
4             if mp[i][k] + mp[k][j] > mp[i][j]//如果点i通过点k这个中转点到点j的距离比原来的距离短，更新距离 
5                 mp[i][j] <- mp[i][k] + mp[k][j]
6     //利用动态规划的思想松弛两点之间的距离

4、分析

Floyd算法总共需要三重循环，第一重循环枚举中介点，第二重循环枚举起点，第三重循环枚举终点，时间复杂度为O(n*n*n)即O(n^3)

因为矩阵的对称性，可以利用上三角优化，但是也仅仅是常数级别的优化。该算法时间复杂度较大，只适合点较少的稠密图。

5、源码

https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/Floyed.cpp

 

 

Dijkstra

1、问题

　　在无向图 G=(V,E) 中，(u,v)代表连接点u与顶点v的边，而w(u,v)代表此边的权重，求两点之间的最短距离。

2、解析

步骤1：设定两个集合S和U，将起点加入到集合S中，其余点加入到集合U中

步骤2：从集合U中寻找一个距离起点最近的点加入到集合S中，并通过该点修改其余点到起点的距离

步骤3：重复步骤二直到所有点均被加入到集合S中

　　

 

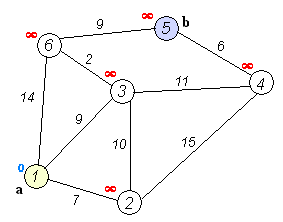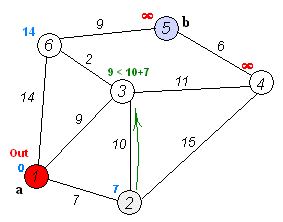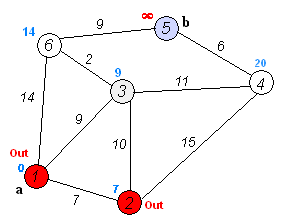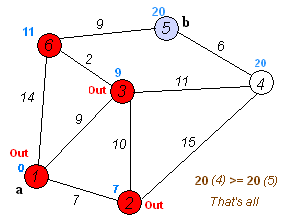
3、设计

 1 void Dijkstra(int mp[][1010],bool* vis,int start,int target,int* dis){
 2     //mp[][]表示两点之间直接相连的距离
 3     //vis[]标记矩阵
 4     //dis[]代表起点到某个点的最短距离 
 5     for i <- 1 to n//初始化数据 
 6         vis[i]=false
 7         dis[i]=inf
 8     vis[start]<-true 
 9     for i <-1 to n
10         dis[i]=mp[start][i]//给起点可直接到达的点赋初值 
11     for i <- 1 to n
12         minn <- inf
13         pos  <- -1
14         for j <- 1 to n
15             if vis[j]==0 and dis[j] < minn//寻找未标记且距离起点最近的点，跟新最小值并记录下该点 
16                 minn <- dis[j]
17                 pos  <- j
18             
19         vis[pos] <- 1
20         for i <- 1 to n
21             if dis[i] > dis[pos] + mp[pos][i]//根据找到的最近点松弛各个点到起点的距离 
22                 dis[i] <- dis[pos] + mp[pos][i]
23             
24 }

4、分析

Dijkstra赋初值时间复杂度O(n)，将n个点逐渐加入到标记集合中需要时间复杂度O(n)，每个点加入到集合后的松弛边操作也需要时间复杂度O(n)，总是时间复杂度O(n^2)。

当然Dijkstra可以用二叉堆或斐波那契堆优化将时间复杂度降到n*log(n)级别

5、源码

https://github.com/ChenyuWu0705/Algorithm-Analyze-and-Design/blob/main/Dijkstra.cpp

posted @ 2021-03-15 19:54  programmer_w  阅读(90)  评论(0)    收藏  举报