CF1648E

题目传送门

题意简述

在一带权无向图上，每次只能连续经过两条边，且代价为两条边边权之和的平方。求单源最短路。

数据范围 \(1\leq n\leq10^5,\ 1\leq m \leq 2\times10^5,\ 1\leq w\leq50\)。

分析

暴力建图的话总边数为 \(m^2\)，会爆炸。

考虑一个路径 \(u\to x\to v\)，\(w_1=w_{u,x},\ w_2=w_{x,v}\)。

由于一次移动至少要经过两条边，所以上述代价和等价于将边权全部移到 \(x\to v\) 上。

如图。

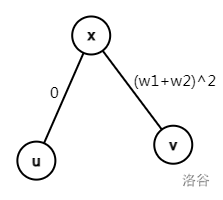
这样的话 \(u\to x\) 就没那么重要了。在 \(w_2\) 一定的情况下共有 \(w=50\) 种可能的权值。

可以考虑以 \(w_1\) 的值构造分层图。

令 \((w,u)\) 为入边边权为 \(w\) 且入点为 \(u\) 的点集。但是由于其并不影响结果，可以将其作为一个点。

则对于点对 \((u,x,v)\)，可以将 \(u\) 向 \((w_1,u)\) 连一条边权为 \(0\) 的边；将 \((w_1,u)\) 向 \(v\) 连一条边权为 \((w_1+w_2)^2\) 的边。

显然 \(u\to v\) 的代价等价于原图。

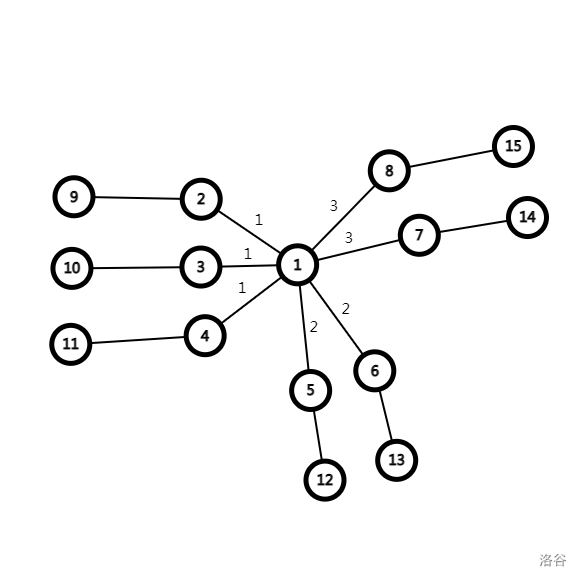
举个例子。

分层前：

分层后：边权什么的可以自己脑补

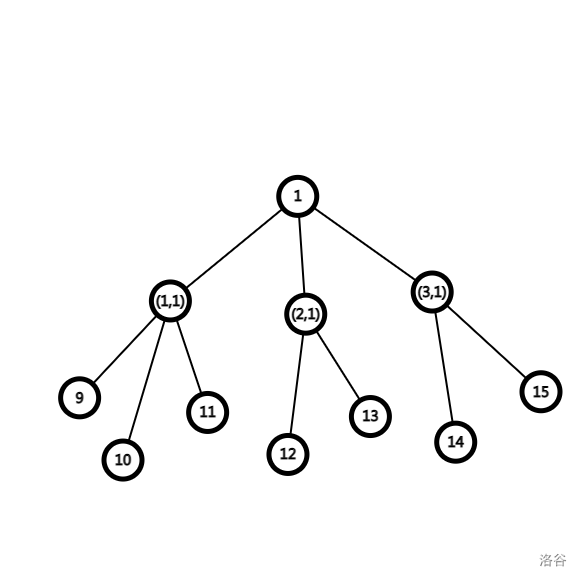
显然，对于一个点 \(u\)（假定其为路径的起始点），分层后其最大出度为 \(w=50\)。

总边数从 \(m^2\) 骤降到了 \(mw\)。

总时间复杂度为 \(O(m\log m)\) 左右。

class Solution {
	struct Graph {
		struct edge {
			int u, v, w, next;
		};
		int head[maxn], idx;
		edge e[maxm];
		void add(int x, int y, int z) {
			idx++; e[idx].u = x, e[idx].v = y, e[idx].w = z;
			e[idx].next = head[x], head[x] = idx;
		}
	} G, revG; 
	struct point {
		int u; ll dis;
		point(int a, ll b) {u = a, dis = b;}
		friend bool operator < (point a, point b) {
			return a.dis > b.dis;
		}
	};
	int n, m;
	std::vector <int> route;
	ll ans[maxn];
	ll dis[maxn];
	bool mk[maxn];
	ll in[maxn], out[maxn];
	void dijkstra(int st, Graph &G) {
		std::priority_queue <point> q;
		for(int i = 1; i <= n; i++) dis[i] = inf, mk[i] = 0;
		dis[st] = 0, q.push(point(st, 0));
		while(!q.empty()) {
			int u = q.top().u; q.pop();
			if(mk[u]) continue;
			mk[u] = 1; route.push_back(u);
			for(int j = G.head[u]; j; j = G.e[j].next) {
				int v = G.e[j].v, w = G.e[j].w;
				if(dis[v] > dis[u] + w) dis[v] = dis[u] + w, q.push(point(v, dis[v]));
			}
		}
	}
	void Count(int st) {
		dijkstra(st, G);
		for(int i = 1; i <= n; i++) in[i] = 0, out[i] = 0;
		in[st] = 1;
		for(auto v : route) {
			for(int i = revG.head[v]; i; i = revG.e[i].next) {
				int u = revG.e[i].v, w = revG.e[i].w;
				if(dis[v] == dis[u] + w) in[v] += in[u], in[v] %= mod;
			}
		}
		std::reverse(route.begin(), route.end());
		for(auto u : route) {
			out[u] = 1;
			for(int i = G.head[u]; i; i = G.e[i].next) {
				int v = G.e[i].v, w = G.e[i].w;
				if(dis[v] == dis[u] + w) out[u] += out[v], out[u] %= mod;
			}
		}
		route.clear();
		for(int i = 1; i <= m; i++) {
			int u = G.e[i].u, v = G.e[i].v, w = G.e[i].w;
			if(dis[v] == dis[u] + w) ans[i] += std::max(1ll, in[u]) * std::max(1ll, out[v]), ans[i] %= mod;
		}
	}
	public: void solve() {
		scanf("%d %d", &n, &m);
		for(int i = 1; i <= m; i++) {
			int u, v, w;
			scanf("%d %d %d", &u, &v, &w);
			G.add(u, v, w), revG.add(v, u, w);
		}
		for(int i = 1; i <= n; i++) Count(i);
		for(int i = 1; i <= m; i++) printf("%lld\n", ans[i]);
	}
}