2020年2月做题报告
2.13号
SP1026 FAVDICE - Favorite Dice
题目大意：
一个n面的骰子，求期望掷几次能使得每一面都被掷到。
solution：
概率DP模板题，掷到任意一点数的概率为 \(\frac{1}{n}\) 。设dp[i]表示已经出现了i面，求答案还需要掷的期望。
易得dp[n]=0，而新掷的骰子可能是没出现过的点数，也可能是出现过的点数
故 dp[i] = dp[i+1] + 1.0*n/(n-i) 最后注意精度即可
int T,n;
double dp[MAXN];
int main(){
in(T);
while(T--){
in(n);
dp[n] = 0;
for(rg int i = n - 1;i >= 0; --i)
dp[i] = dp[i + 1] + 1.0 * n / (n - i);
printf("%.2f\n",dp[0]);
}
return 0;
}
P1291 [SHOI2002]百事世界杯之旅
题目大意：一个n面的骰子，求期望掷几次能使得每一面都被掷到。输出需要以假分数形式输出
solution：与SP1026基本一样，只是答案需要分别记录分子和分母，输出有点复杂。
int n;
ll so,mo,N; //so分子 mo分母
inline ll get(ll x){//获取位数
ll s = 0;
while(x){
++s;
x /= 10;
}
return s;
}
int main(){
in(n),mo = 1;//分母设为1防止出错。分子为0
for(rg int i = n - 1;i >= 0; --i){
so = (n - i)*so + mo*n;// y/x+b/a=(ay+bx)/ax 通分
mo *= n-i;
int tmp = gcd(so,mo);//约分
so /= tmp,mo /= tmp;
}
if(!(so % mo)){//如果答案为整数
outn(so / mo);
return 0;
}
//否则答案为分数
ll tmp = gcd(so,mo);
so /= tmp,mo /= tmp;//约分
N = so/mo,so %= mo;//N为整数部分，分数化为真分数
ll kong = get(N);//获取空格
ll gang=get(mo);//组成分数线的'-'的个数为分母的长度
for(rg int i = 1;i <= kong; ++i)//输出分子前导空格
printf(" ");
outn(so);//输出分子并换行
out(N);//输出整数部分
for(rg int i = 1;i <= gang; ++i)//输出分数线
printf("-");
puts("");//换行
for(rg int i = 1;i <= kong; ++i)//输出分母前导空格
printf(" ");
out(mo);//输出分母
return 0;
}
2.15
P4550-收集邮票
题目大意：
如题
solution：
\(E{(X)} = \sum P{(i)} \times X{(i)}\) ，也就是 \(E{(X)} = \sum \text{概率} \times \text{权值}\)
根据定义，设
\(a[i]\)表示现在取到\(i\)张邮票，要取完剩下邮票的期望 次数
\(a[i] = \frac{i}{n}\times a[i]\ +\ \frac{n-i}{n}\times a[i+1]\ +\ 1\)
\(b[i]\)表示现在取到\(i\)张邮票，要取完剩下邮票的期望 价格
\(b[i] = \frac{i}{n}\times(b[i]+a[i]+1)\ +\ \frac{n-i}{n}\times(b[i+1]+a[i+1]+1)\)
显然最后输出 \(b[0]\) 即可
int T,n;
double a[MAXN],b[MAXN];
int main(){
in(n);
a[n] = b[n] = 0;
for(rg int i = n - 1;i >= 0; --i){
double p1 = 1.0 * i / n;
double p2 = 1.0 * (n - i) / n;
a[i] = (p2 * a[i + 1] + 1) / (1 - p1);
b[i] = (b[i + 1] * p2 + a[i] * p1 + a[i + 1] * p2 + 1) / (1 - p1);
}
printf("%.2f\n",b[0]);
return 0;
}
2.16
P1962-斐波那契数列
solution：
虽然普通斐波那契数列可以用递归来实现，但是在这个地方由于数据极大，故需要 矩阵快速幂 解决。
通过推导得知，设初始矩阵为 \([F1\ F2]\) ，即 \([1\ 1]\)，而快速幂中
$base = $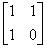 
故答案为 \([1\ 1] \times(\) 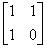^ \(^{n-2}\)
ll n;
struct Matrix{
ll m[MAXN][MAXN]; //矩阵数组m
Matrix(){
memset(m, 0, sizeof(m));
}
};
inline Matrix multiply(Matrix x, Matrix y) //定义矩阵相乘的函数{
Matrix res; //存结果的矩阵
for(rg int k = 1;k <= 2; ++k)
for(rg int i = 1;i <= 2; ++i)
for(rg int j = 1;j <= 2; ++j)
res.m[i][j] = (res.m[i][j] + x.m[i][k] * y.m[k][j] % mod) % mod;
return res;
}
inline Matrix helper(Matrix a, ll p) //矩阵a的pow次方{
Matrix b;
for(int i = 1;i <= 2; ++i) //单位矩阵
b.m[i][i] = 1;
while(p){
if(p & 1)
b = multiply(b,a);
a = multiply(a, a);
p >>= 1;
}
return b;
}
int main(){
Matrix a,b;
in(n);
a.m[1][1] = 0,a.m[1][2] = 1,a.m[2][1] = 1,a.m[2][2] = 1;
b.m[1][1] = 1,b.m[1][2] = 1;
Matrix ans = helper(a, n-1);
ans = multiply(b, ans);
out(ans.m[1][1]);
return 0;
}
P1939 -【模板】矩阵加速（数列）
模板
P3758-[TJOI2017]可乐
设原图邻接矩阵为矩阵\(G\)
从\(Floyd\)角度进行考虑，在\(G^k\)
中，\((i,j)\)的元素即： 从\(i\)走\(k\)步到\(j\)的路径方案总数
故 \(G^{t}\) 的第一行的和即为答案
ll n,m,t,ans;
struct Matrix{
ll m[kMaxN][kMaxN];
Matrix(){
memset(m , 0 , sizeof(m));
}
}Start,calc;
inline Matrix Multiply(Matrix x,Matrix y){
Matrix res;
for(rg ll k = 0;k <= n; ++k)
for(rg ll i = 0;i <= n; ++i)
for(ll j = 0 ; j <= n ; j++ )
res.m[i][j] = (res.m[i][j] + x.m[i][k] * y.m[k][j] % Mod) % Mod;
return res;
}
inline Matrix ksm(Matrix a,ll Pow){
Matrix ans;
for(rg ll i = 1;i <= n; ++i)
ans.m[i][i] = 1;
while(Pow != 0){
if((Pow & 1) == 1)
ans = Multiply(ans,a);
a = Multiply(a,a);
Pow >>= 1;
}
return ans;
}
int main(){
in(n),in(m);
for(rg ll i = 1;i <= m; ++i){
ll u = read(),v = read();
Start.m[u][v] = 1;
Start.m[v][u] = 1;
}
in(t);
for(rg ll i = 0;i <= n; ++i)
Start.m[i][i] = 1;
for(rg ll i = 1;i <= n; ++i)
Start.m[i][0] = 1;
calc = ksm(Start , t);
for(rg ll i = 0;i <= n; ++i){
ans += calc.m[1][i];
ans %= Mod;
}
outn(ans);
return 0;
}
2.18
P3197-[HNOI2008]越狱
题目大意：
N个牢房，每个牢房一个犯人，有M种宗教，每个犯人可能信仰其中一种。如果相邻牢房的犯人的宗教相同，就可能发生越狱，求有多少种状态可能发生越狱。
solution：
答案 = 每个犯人宗教状态总数 - 任意相邻牢房的犯人宗教都不同总数。
即\(ans = m^n - m\times(m-1)^{n-1}\)
int main()
{
in(m),in(n);
ans = (ksm(m,n) - m*ksm(m-1,n-1)%mod + mod) % mod;
outn(ans);
return 0;
}
2.19
P3389-【模板】高斯消元法
模板题，找阶梯矩阵即可
P4910-帕秋莉的手环
题目大意：
黑白两种颜色的珠子各\(inf\)颗，选取\(n\)颗串成环，使环中任意一对相邻的棋子中至少有一个黑色。两种经过反转后重合的方案视为不同的方案
solution：
推算之后，答案为 （首黑，尾黑的答案数） + \(2\times\)（首黑，尾白）
然后再找到dp递推式，然后再用矩阵乘法解决即可
int T,tot;
ll n;
struct Matrix{
ll m[kMaxN][kMaxN];
Matrix(){
memset(m, 0, sizeof(m));
}
}st,trans;
inline Matrix Multiply(Matrix x, Matrix y){
Matrix res;
for(rg int k = 1; k <= 2; ++k)
for(rg int i = 1; i <= 2; ++i)
for(rg int j = 1; j <= 2; ++j)
res.m[i][j] = (res.m[i][j] + x.m[i][k]*y.m[k][j] % Mod) % Mod;
return res;
}
inline Matrix ksm(Matrix a, ll Pow){
Matrix ans;
for(int i = 1; i <= 2; ++i)
ans.m[i][i] = 1;
while(Pow != 0){
if(Pow & 1)
ans = Multiply(ans, a);
a = Multiply(a, a);
Pow >>= 1;
}
return ans;
}
int main(){
in(T);
st.m[1][2] = 2;
st.m[2][2] = 1;
trans.m[1][2] = trans.m[2][1] = trans.m[2][2] = 1;
for(rg int i = 1; i <= T; ++i){
in(n);
Matrix ans;
ans = ksm(trans, n-1);
ans = Multiply(st, ans);
tot = ans.m[1][1] + ans.m[2][2];
tot %= Mod;
outn(tot);
}
return 0;
}
2.21
P3812-【模板】线性基
模板题
2.22
P3376-【模板】网络最大流
模板题
P2740-[USACO4.2]草地排水Drainage Ditches
模板题，使用Dinic。找分层图的时候需要注意
2.23
P2065-[TJOI2011]卡片
二分图。部分分解法很容易得到：两张不同颜色的卡牌只要可以组成一对就连边，最后跑网络流。 但是 \(N^2\) 建图会TLE，我们可以新建一列点数为质因数的点，将每个卡牌的点数分解质因数将卡牌与其质因数连边，从蓝卡连到质因数，再连到红卡，流量为 \(inf\) 即可。
Dinic模板和跑分层图函数就不放了。
inline void blue(int now, int id)//蓝卡连点
{
for(rg int i = 1;i<=cnt && prim[i]<=now; ++i)
if(!(now % prim[i]))
{
add(id, i+t, inf);
while(!(now % prim[i]))
now /= prim[i];
}
}
inline void red(int now, int id)//红卡连点
{
for(rg int i = 1;i<=cnt && prim[i]<=now; ++i)
if(!(now % prim[i]))
{
add(i+t, id, inf);
while(!(now % prim[i]))
now /= prim[i];
}
}
int main(){
prime();
int T = read();
while(T--){
memset(head, 0, sizeof(head));
memset(to, 0, sizeof(to));
memset(nxt, 0, sizeof(nxt));
memset(edge, 0, sizeof(edge));
tot = 1, maxflow = 0;
in(m),in(n);
s = 0, t = n+m+1;
for(rg int i = 1;i <= m; ++i)
add(s, i, 1),blue(read(), i);
for(rg int i = 1;i <= n; ++i)
add(i+m, t, 1),red(read(), i+m);
while(bfs())
maxflow += dinic(s, inf);
outn(maxflow);
}
return 0;
}
P2472-[SCOI2007]蜥蜴
这里需要 拆点 ，由于每根柱子只能经过一定次数，故将拆点拆出来的边容量设为主子高度，源点与最开始蜥蜴在的地方连容量为\(1\)的边，所有能够一次性跳出去的点与汇点连容量为\(inf\)的边。跑最大流即可。
inline int calc(int x, int y)
{
return (x-1) * m + y;
}
int main()
{
int cnt = 0; //
in(n), in(m), in(d);
tot = 1;
s = 0, t = (n*m*2) + 1;
for(rg int i = 1; i <= n; ++i)
for(rg int j = 1; j <= m; ++j)
{
char c;
cin>>c;
dis[i][j] = (int)(c - '0');
if(dis[i][j])
{
int tmp = calc(i, j);
add(tmp, tmp+n*m, dis[i][j]); //拆点
}
}
for(rg int i = 1; i <= n; ++i)
for(rg int j = 1; j <= m; ++j)
{
char c;
cin>>c;
if(c == 'L')
{
cnt++;
add(s, calc(i, j), 1); //源点到L
}
}
for(rg int i = 1; i <= n; ++i)
for(rg int j = 1; j <= m; ++j)
{
//if(!dis[i][j])
// continue; //不能跳过，否则下面无法连边
if(dis[i][j] && (min(i, n-i+1) <= d || min(j, m-j+1) <= d)) //超出下界和右界没算清楚
add(calc(i, j) + m * n, t, inf); //
for(rg int k = 1; k <= n; ++k)//
for(rg int p = 1; p <= m; ++p)//
{
if(abs(k-i) + abs(p-j) > d)
continue;
if(!dis[k][p])
continue;
add(calc(i, j) + m * n, calc(k, p), inf); //
}
}
int flow = 0;
while(bfs()) //对每一次残余网络找一次分层图
{
flow = dinic(s, inf);
maxflow += flow;
}
outn(cnt - maxflow);
return 0;
}
2.24
P3381-【模板】最小费用最大流
模板题
2.25
P2762-太空飞行计划问题
从 \(S\) 到 实验 连一条容量为 收益 的边。
从 实验 到 器材 连一条容量为 \(inf\) 的边。
从 仪器 到 \(T\) 连一条容量为 消耗 的边。
然后跑最大权闭合子图即可
int head[N], to[M], edge[M], nxt[M], pre[N], level[N];
int n, m, s, t, tot, maxflow;
int val[N], cost[N], ans;
int main()
{
in(n), in(m);
s = 0, t = n+m+1; // 源点、汇点
tot = 1;
for(rg int i = 1;i <= n; ++i)
{
in(val[i]);
add(s, i, val[i]);
ans += val[i];
char s[10000 + 2];
memset(s, 0, sizeof(s));
cin.getline(s, 10000);
int tmp = 0, num;
while(sscanf(s+tmp, "%d", &num) == 1)
{
add(i, num+n, inf);
if(!num)++tmp;
else
while(num)
{
num /= 10;
++tmp;
}
++tmp;
}
}
for(rg int i = 1;i <= m; ++i)
{
in(cost[i]);
add(i+n, t, cost[i]);
}
int flow = 0;
while(bfs())
{
flow = dinic(s, inf);
while(flow)
{
maxflow += flow;
flow = dinic(s, inf);
}
}
for(rg int i = 1;i <= n; ++i)
if(level[i])
out(i);
puts("");
for(rg int i = 1;i <= m; ++i)
if(level[i + n])
out(i);
puts("");
outn(ans - maxflow);
return 0;
}
2.26
P417-[NOI2006]最大获利
\(S\) 向 用户 连容量为 收益 的边
中转站 向 \(T\) 连容量为 成本 的边
用户 向 需要的中转站 连容量为 \(inf\) 的边
然后跑最大权闭合子图，输出 中转站建立费用和 \(减去\) 最大流 即可。
int main()
{
in(n), in(m); // 源点、汇点
s = 0, t = n+m+1, tot = 1;
for(rg int i = 1; i <= n; ++i)
{
int x = read();
add(i, t, x);
}
for(rg int i = 1; i <= m; ++i)
{
int x = read(), y = read(), z = read();
add(i+n, x, inf);
add(i+n, y, inf);
add(s, i+n, z);
ans += z;
}
int flow = 0;
while(bfs()) //对每一次残余网络找一次分层图
{
flow = dinic(s, inf);
maxflow += flow;
}
outn(ans - maxflow);
return 0;
}
2.27
P3410-拍照
\(S\) 向 方案编号 连容量为 方案收益 的边
下属编号 向 \(T\) 连容量为 下属支出 的边
方案编号 向 对应下属 连容量为 \(inf\) 的边
然后跑最大权闭合子图，输出 方案价值和 \(减去\) 最大流 即可。
int main()
{
in(n), in(m);
s = 0, t = n+m+1;
tot = 1;
for(rg int i = 1; i <= n; ++i)
{
int v = read();
add(s, i, v);
ans += v;
int x;
while(x = read(), x)
add(i, x+n, inf);
}
for(rg int i = 1; i <= m; ++i)
{
int x = read();
add(i+n, t, x);
}
int flow = 0;
while(bfs())
{
flow = dinic(s, inf);
while(flow)
{
maxflow += flow;
flow = dinic(s, inf);
}
}
outn(ans - maxflow);
return 0;
}
算法总结:
概率与期望：
这一类型的题目通常使用 \(DP\) 解决，设定状态与状态转移方程很重要。概率与期望对于数学水平要求有一定高度，还需要好好练一练
高斯消元：
高斯消元原本适用于解多元一次方程，但是在提高组难度及以上的题目中，通常都会考察高斯消元的基本定义。要灵活得将题目元素对应成高斯消元。
网络流
最小权闭合子图、最小割、最小费用最大流、二分图这些算法虽然都可以用最大流来解决，但是本质不同，且不同题目的应用也不同。
在大部分题目中，考察的都是算法识别能力以及如何按照题目建图（如隐士图）。
浙公网安备 33010602011771号