第一课:基本概念
数据结构(data structure)是计算机中存储、组织数据的方式。通常情况下,精心选择的数据结构可以带来最优效率的算法。
例1:如何在书架上摆放图书
怎么插入
怎么查找
方法一:随便放,容易插入,不易查找
方法二:拼音字母顺序排放,不易插入,容易查找
方法三:按书类别划分区域排放,容易插入,容易查找,问题:空间分配,类别粗细
解决问题方法的效率,跟数据的组织方式有关。
例2:写程序实现PrintN
方法一:直接打印
void PrintN(int N)
{
int i;
for (i = 1;i <= N;i++)
{
printf("%d\n",i);
}
return;
}方法二:递归打印
void PrintN(int N)
{
if (N) {
PrintN(N - 1);
printf("%d\n",N);
}
return;
}令N = 10,100,1000,10000,100000。
递归打印100000,内存空间全占用
解决问题方法的效率,跟空间的利用效率有关
例3:写程序计算给定多项式在定点x处的值
f(x) = a0+a1x+a2x2+.......+anxn
方法一:直接写
double f(int n,double a[],double x)
{
int i;
double p = a[];
for (i = 1;i <= n;i++)
{
P += (a[i] * pow(x,i));
}
return p;
}方法二:巧用结合律
double f(int n,double a[],double x)
{
int i;
double p = a[n];
for (i = n;i > 0;i--)
p = a[i-1] + x * p;
return p;
}计时器
#include <stdio.h>
#include <time.h>
#include <math.h>
#define MAXK 1e6
#define MAXN 101
clock_t start,stop;
double duration;
double f1(int n,double a[],double x)
{
int i;
double p = a[0];
for (i = 1;i <= n;i++)
{
p += (a[i] * pow(x,i));
}
return p;
}
double f2(int n,double a[],double x)
{
int i;
double p = a[n];
for (i = n;i > 0;i--)
p = a[i-1] + x * p;
return p;
}
int main(void)
{
int i = MAXK;
int j = MAXN;
double a[MAXN];
double dration1,dration2;
for (j = 0;j < MAXN; j++)
{
a[j] = 1.0 / j;
}
start = clock();
while (i--)
{
printf("wait1:%d\n",i);
f1(MAXN - 1,a,1.1);
}
stop = clock();
dration1 = ((double)(stop - start)) / CLK_TCK / MAXK;
i = MAXK;
start = clock();
while (i--)
{
printf("wait2:%d\n",i);
f2(MAXN - 1,a,1.1);
}
stop = clock();
dration2 = ((double)(stop - start)) / CLK_TCK / MAXK;
printf("dration1 = %6.2e\n",dration1);
printf("dration2 = %6.2e\n",dration2);
return 0;
}
#include <stdio.h>
#include <time.h>
#include <math.h>
#define MAXK 1e6
#define MAXN 101
clock_t start,stop;
double duration;
typedef double(*MyFunc)(int,double *,double);
double f1(int n,double a[],double x)
{
int i;
double p = a[0];
for (i = 1;i <= n;i++)
{
p += (a[i] * pow(x,i));
}
return p;
}
double f2(int n,double a[],double x)
{
int i;
double p = a[n];
for (i = n;i > 0;i--)
p = a[i-1] + x * p;
return p;
}
double clock_time(MyFunc f,int n,double a[],double x)
{
int i = MAXK;
double dration;
start = clock();
while (i--)
{
f(n,a,x);
//printf("wait:%d\n",i);
}
stop = clock();
dration = ((double)(stop - start)) / CLK_TCK / MAXK;
return dration;
}
int main(void)
{
int i;
double a[101];
for (i = 0;i < MAXN;i++)
{
a[0] = 1.0 / i;
}
printf("ticks1 = %6.2e\n",clock_time(f1,MAXN,a,1.1));
printf("ticks2 = %6.2e\n",clock_time(f2,MAXN,a,1.1));
return 0;
}/* 2023.04.10 */
抽象数据类型
数据类型:
- 数据对象集
- 数据集合相关联的操作集合
抽象:描述数据类型的方法不依赖于具体实现
- 与存储数据的机器无关
- 与数据存储的物理结构无关
- 与实现操作的算法和编程语言均无关
只描述数据对象集和相关操作及“是什么”,并不涉及“如何做到”的问题
注:通用,不关心具体的存储方式,不关心具体的实现方法
算法:
- 一个有限指令集
- 接受一些输入(有些情况不需要输入)
- 产生输出
- 一定在有限步骤后终止
- 每一条指令必须:
- 有充分明确的目标,不可以有歧义
- 计算机能处理的范围之内
- 描述应不依赖于任何一种计算机语言以及具体的实现手段
什么是好的算法:
空间复杂度:占用存储空间的长度。
注:所用的方法要花多少空间完成目标
时间复杂度:耗费时间的长度。
注:所用方法要花多少时间完成目标
例二
void PrintN(int N)
{
if (N) {
PrintN(N - 1);
printf("%d\n",N);
}
return;
}递归函数会存储调用函数前的所有状态
S(N) = C * N;
/* 2023.04.11 */
例3
double f(int n,double a[],double x)
{
int i;
double p = a[];
for (i = 1;i <= n;i++)
{
P += (a[i] * pow(x,i));
}
return p;
}pow(x,i) :执行了(1 + 2 + .... + n)= (n + n^2)/ 2次乘法:T(n) = C1n2 + C2n
double f(int n,double a[],double x)
{
int i;
double p = a[n];
for (i = n;i > 0;i--)
p = a[i-1] + x * p;
return p;
}n次乘法:T(n) = n
一层循环解题思路:
解题思路:
1、列出循环档数t及每轮循环的变化值;
2、找到t与i的关系
3、确定循环停止条件
4、联立两式,接方程
5、写结果
二分法:
t:0,1,2,3........
i:n,n/2,n/4........
1:i = n/2t
2:i = 1
联立1、2两式 n/2t = 1
T = O(log2n)
/* 2023.04. 17 */
复杂度的渐进表示法
T(n) = O(f(n)),表示存在常数C>0,n0>0,使得当n>n0时,有T(n) <= C * f(n),即存在某上界C * f(n),始终大于T(n);
T(n) = Ω(g(n)),表示始终存在C>0,n0>0,使得当n>n0,有T(n) >= C * f(n),即存在某下界C * f(n),始终小于T(n);
T(n) = Θ(h(n)),表示同时有T(n) = O(h(n))和T(n) = Ω(h(n)),即存在C * f(n),始终等于T(n)。
上界和下界可以有无穷多个,一般写最小上界,最大下界。
复杂度分析小窍门(代码)
若两段算法分别有复杂度T1(n) = O(f1(n))和T2(n) = O(f2(n)),则
T1(n) + T2(n) = max(O(f1(n)),O(f2(n)))
T1(n) * T2(n) = O(f1(n) * f2(n))
若T(n)是关于n的k阶多项式,那么T(n) = Θ(nk)
一个for循环的时间复杂度等于循环次数乘以循环体代码的复杂度
if - else 结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度,总体复杂度取三者中最大
/* 2023.04. 25 */
int MaxSubseqsuml(int A[],int N)
{
int ThisSum,MaxSun = 0;
int i.j.k;
for (i = 0;i < N;j++)
{
for (j = i;j < N;j++)
{
ThisSum = 0;
for (k = i;k <= j;k++)
{
ThisSum += A[k];
if (ThisSum > MaxSum)
MaxSum = ThisSum;
}
}
}
return MaxSum;
}/* 2023.04. 26 */
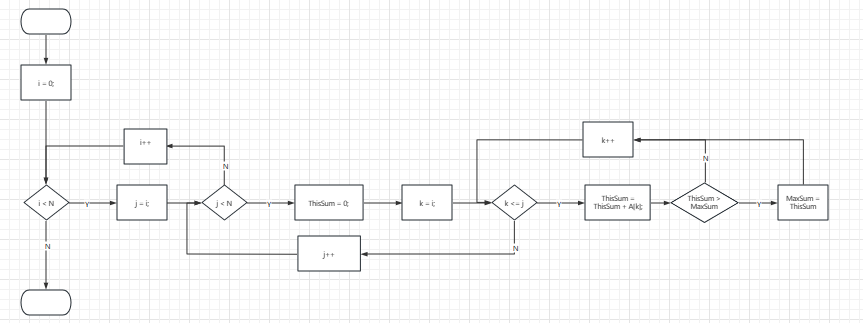
/* 2023.04. 27 */
int MaxSubseqsuml(int A[],int N)
{
int ThisSum,MaxSun = 0;
int i,j,k;
for (i = 0;i < N;j++)
{
ThisSum = 0;
for (j = i;j < N;j++)
{
ThisSum += A[k];
if (ThisSum > MaxSum)
MaxSum = ThisSum;
}
}
return MaxSum;
}分而治之
注:"?" 在C语言中表示疑问、假如、如果,相当于if。":"在C语言中表示判断的结果选择,相当于else。例如,a > b ? y : n。如果A大于B那么选择y结果,否则选择n结果。
inf Max3(int A,int B,int C)
{
return A>B ? A>C ? A : C : B>C ? B : C;
}
int DibideAndConquer(int List[],int left,int right)
{
int MaxLeftSum,MaxRightSum;
int MaxLeftBorderSum,MaxRightBorderSum;
int LeftBorderSun,RightBorderSum;
int center,i;
if (left == right)
{
if (List[left] > 0)
return Lift[left];
else
return 0;
}
center = (left + right) / 2;
MaxLeftSum = DivideAndConquer(List,left,center);
MaxRightSum = DivideAndConquer(List,Right,center);
MaxLeftBorderSum = 0;
LeftBordetSum = 0;
for (i = center;i >= left;i--)
{
LeftBorderSum += Lisr[i];
if (LeftBorderSum > MaxLeftBorderSum)
{
MaxLeftBorderSum = LeftBorderSum;
}
}
MaxRightBorderSum = 0;
RightBorderSum = 0;
for (i = center;i <= right;i++)
{
RightBorder += List[i];
if (RightBorderSum > MaxRightBorderSum)
{
MaxRightBorderSum > RightBorderSum;
}
}
return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum + MaxRightBorderSum);
}
int MaxSubseqSum3(int List[],int N)
{
return DivideAndConquer(List,0,N - 1);
}若记整体时间复杂度为T(N),则函数DivideAndConquer中递归进行“分”的复杂度为2T(N/2),;因为我们解决了2个长度减半的子问题。求跨分界线的最大子列和时,有两个简单的for循环,所用步骤一共不超过N,所以可在O(N)时间完成,其他步骤都只需常数O(1)时间,综上分析有递推式:
T(1) = O(1);
T(N)
= 2(T(N / 2)) + O(N)
= 2[2(T(N / 2 / 2)) + O(N / 2)] + O(N)
=22 T(N / 22) + 2O(N)
=....=
=2k T(N / 2K) +k * O(N)
当程序走完,即N / 2k = 1时,k = log N
T(N)
= N * T(1) + log N * O(N)
= N * T(1) + O (Nlog N)
= O(Nlog N)
在线处理
int MaxSubseqSum4(int A[],int N)
{
int ThisSum,MaxSum;
int i;
ThisSum = MaxSum = 0;
for (i = 0;i < N;i++)
{
ThisSum += A[i];
if (ThisSum = MaxSum)
MaxSum = ThisSum;
else if (ThisSum < 0)
ThisSum = 0;
}
return MaxSum;
}"在线"的意思时指每输入一个数据就进行即时处理,在任何一个地方中止输入,算法都能正确给出当前的解。(给一个算一个)。
算法2程序
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
int MaxSubseqsum2(int A[],int N);
int main()
{
int *List = NULL;
int N;
int i;
scanf("%d",&N);
List = (int *)malloc(sizeof(int) * N);
for (i = 0;i < N;i++)
{
scanf("%d",&List[i]);
}
printf("%d",MaxSubseqsum2(List,N));
return 0;
}
int MaxSubseqsum2(int A[],int N)
{
int ThisSum,MaxSum = 0;
int i,j;
for (i = 0;i < N;i++)
{
ThisSum = 0;
for (j = i;j < N;j++)
{
//printf("%d\n",j);
ThisSum += A[j];
if (ThisSum > MaxSum)
MaxSum = ThisSum;
}
}
return MaxSum;
}算法3程序
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
int Max3(int A,int B,int C);
int MaxSubseqSum3(int A[],int N);
int main()
{
int *List = NULL;
int N;
int i;
scanf("%d",&N);
List = (int *)malloc(sizeof(int) * N);
for (i = 0;i < N;i++)
{
scanf("%d",&List[i]);
}
printf("%d",MaxSubseqSum3(List,N));
return 0;
}
int Max3(int A,int B,int C)
{
return A>B ? A>C ? A : C : B>C ? B : C;
}
int DivideAndConquer(int List[],int left,int right)
{
int MaxLeftSum,MaxRightSum;
int MaxLeftBorderSum,MaxRightBorderSum;
int LeftBorderSum,RightBorderSum;
int center,i;
if (left == right)
{
if (List[left] > 0)
return List[left];
else
return 0;
}
center = (left + right) / 2;
MaxLeftSum = DivideAndConquer(List,left,center);
MaxRightSum = DivideAndConquer(List,center + 1,right);
//printf("MaxRightSum:%d\n",MaxRightSum);
//printf("MaxRightSum:%d\n",MaxRightSum);
MaxLeftBorderSum = 0;
LeftBorderSum = 0;
for (i = center;i >= left;i--)
{
LeftBorderSum += List[i];
if (LeftBorderSum > MaxLeftBorderSum)
{
MaxLeftBorderSum = LeftBorderSum;
}
//printf("MaxLeftBorderSum:%d\n",MaxLeftBorderSum);
}
MaxRightBorderSum = 0;
RightBorderSum = 0;
for (i = center + 1;i <= right;i++)
{
RightBorderSum += List[i];
if (RightBorderSum > MaxRightBorderSum)
{
MaxRightBorderSum = RightBorderSum;
}
// printf("MaxRightBorderSum:%d\n",MaxRightBorderSum);
}
return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum + MaxRightBorderSum);
}
int MaxSubseqSum3(int List[],int N)
{
return DivideAndConquer(List,0,N - 1);
}算法4程序
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
int MaxSubseqSum4(int A[],int N);
int main()
{
int *List = NULL;
int N;
int i;
scanf("%d",&N);
List = (int *)malloc(sizeof(int) * N);
for (i = 0;i < N;i++)
{
scanf("%d",&List[i]);
}
printf("%d",MaxSubseqSum4(List,N));
return 0;
}
int MaxSubseqSum4(int A[],int N)
{
int ThisSum,MaxSum;
int i;
ThisSum = MaxSum = 0;
for (i = 0;i < N;i++)
{
ThisSum += A[i];
if (ThisSum > MaxSum)
MaxSum = ThisSum;
else if (ThisSum < 0)
ThisSum = 0;
}
return MaxSum;
}/* 2023.05. 01 */
课后作业
Maximum Subsequence Sum
#include <stdio.h>
#include <stdlib.h>
int main()
{
int k;
int *data;
int i;
int start,end,sum,temp,tempi,tempj;
while (scanf("%d",&k) != EOF)
{
data = (int *)malloc(k * sizeof(int));
for (i = 0;i < k;i++)
{
scanf("%d",&data[i]);
}
sum = 0;
start = 0;
end = k - 1;
temp = 0;
tempi = 0;
tempj = 0;
for (i = 0;i < k;i++)
{
if (temp >= 0)
{
temp += data[i];
tempj = i;
}
else
{
temp = data[i];
tempi = i;
tempj = i;
}
if (temp > sum || (temp == 0 && end == k - 1))
{
sum = temp;
start = tempi;
end = tempj;
}
}
printf("%d %d %d\n",sum,data[start],data[end]);
}
return 0;
}/* 2023.05. 03 */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号