激活函数
学习神经网络时,一直对激活函数感觉懵懂,最近看了李宏毅的课程,感受颇多。
神经网络可以解决线性回归里不能解决的非线性问题,但究竟是如何实现线性到非线性的转换?
1. 先回忆一下线性的形式
y=wx+b,w为权值weight,b为阈值(或偏置)bias。拟合出来的线条是一条直线,b是为了修正wx和y的偏差的。当问题复杂化后,一个简单的线性函数无法描述问题,那么如何描述这类非线性问题?
2. 非线性的转换
下图(图1)中,y和x呈非线性关系,构成一个分段函数。
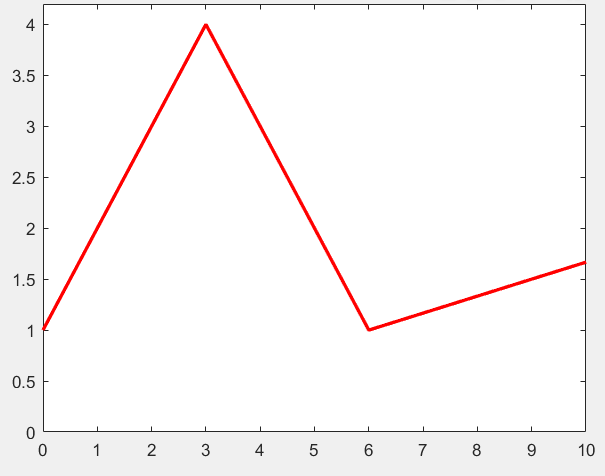
对于这样的函数,仅用一个y=wx+b是无法拟合的,因此引入了一种分段函数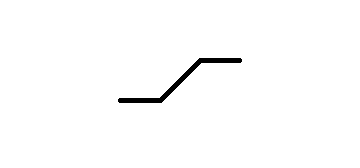
,目的是为了在原来的函数中加入非线性。
接下来,就是见证奇迹的时候。李宏毅在这里很巧妙的讲解了非线性的构造,我们只需将这个分段函数进行一定的变换,再相加就可得到上图中的红线。简单的理解就是,一个复杂的非线性图像可以由几个经过变换的分段函数叠加后得到,这也就是激活函数的作用,所以我们才要引入这个概念。激活函数增加了非线性,扩充了机器学习对现实例子的拟合范围。
下图中(图2)展示了如何用几个激活函数叠加得到目标函数:
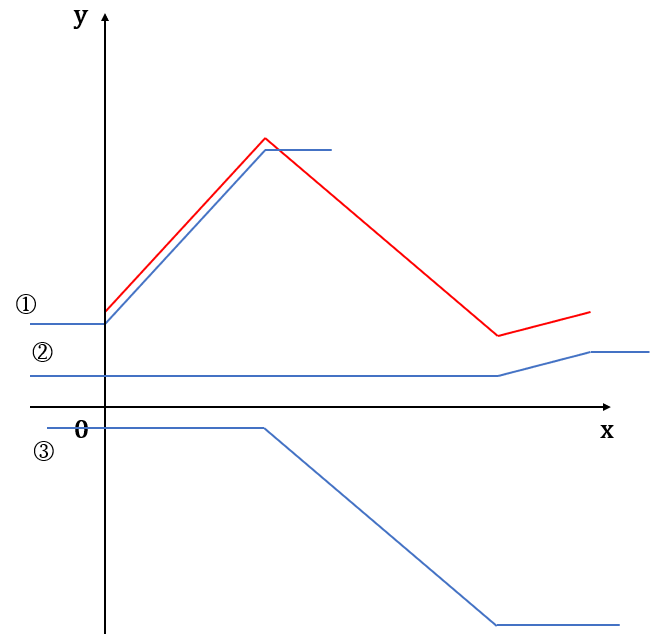
图中的三条蓝色线条经过平移后,再进行叠加,即可得到红色线条。而三个蓝色的图像都可以由原始的激活函数做变换而来,下面用 sigmoid函数来说明。
sigmoid是机器学习中最常用的激活函数之一,它的表达式为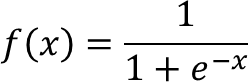
令y=c·sigmoid(b+wx),即
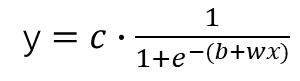
通过改变c,b,w的值即可对图形进行变换,下面用图像来直观地感受一下。
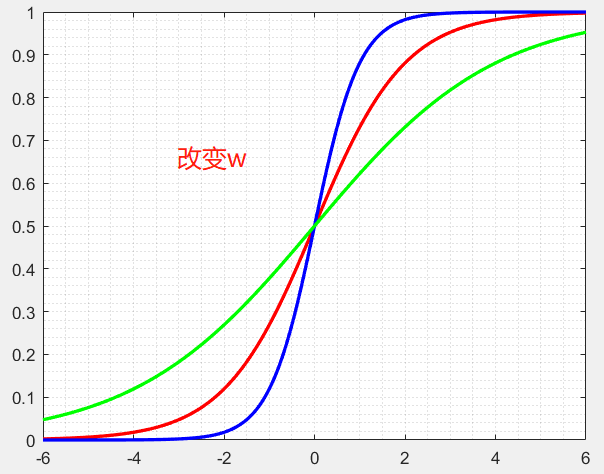
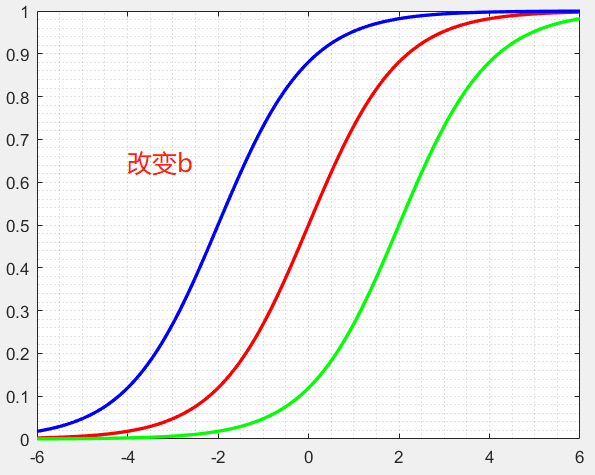
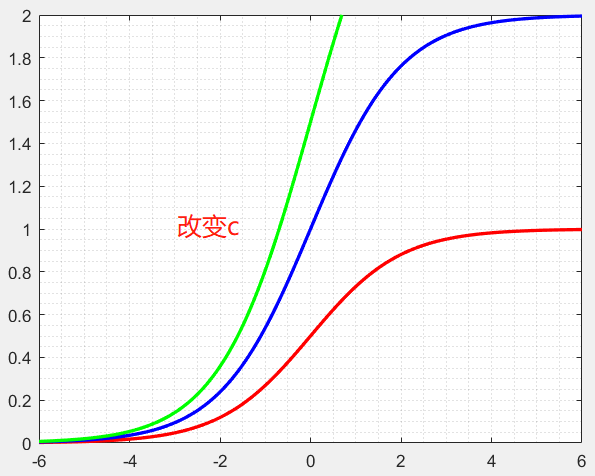
回到我们的图2,图中的①,②,③分别选取不同的c,b,w可以得到,我们可以写出他们的表达式,假设激活函数为sigmoid,则
①式: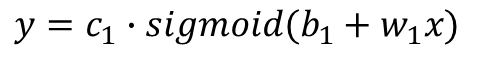
②式: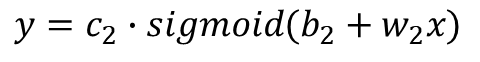
③式: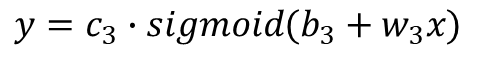
3. 带激活函数的表达式
最终,我们可以得到一个用激活函数来表示的非线性函数表达式:
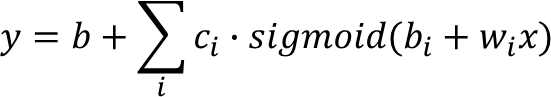


 浙公网安备 33010602011771号
浙公网安备 33010602011771号