2025.7.3 闲话

山河重整对着 Durfee Square 疯狂 abcdefg 一万年发现要算的分拆数有额外限制.jpg

以下所描述的（互异）分拆数计算方法可以通过枚举 \(h\) 来做到 \(O(n\sqrt n)\) 求前 \(n\) 项 .

分拆数

Durfee Square 分解：

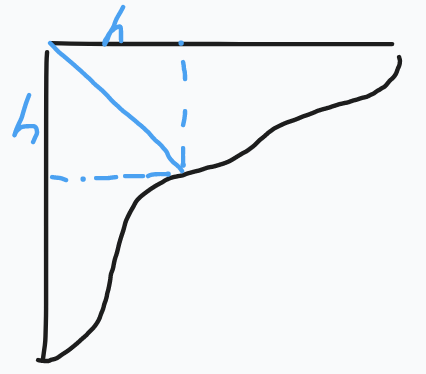
\[\prod_{k\ge1}\dfrac1{1-x^k}=\sum_{h\ge0}x^{h^2}\left(\prod_{k=1}^h\dfrac1{1-x^k}\right)^2 \]

可以理解为在 Ferrers 图上枚举从原点引出的斜线长度 .

互异分拆数

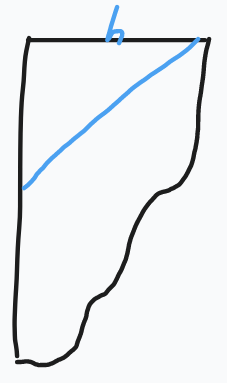
\[\prod_{i\ge1}(1+x^i)=\sum_{h\ge 0}x^{h(h+1)/2}\prod_{i=1}^h\dfrac1{1-x^i} \]

可以理解为枚举选了多少个数然后 \(a_i\gets a_i-i\) 转为普通分拆数 .

图