2025.4.1 闲话

学习了一下高端反射容斥（

比如我们要处理这样一个问题：从 \((0,s)\) 走到 \((m,t)\)，其中需要随时保证 \(1\le y\le n\) .

大概就是考虑没限制可以简单 DP 处理，如果在圆环上做 DP，一边放正的贡献、一边放负的贡献，那么它们碰到边界就会消掉，这样就能处理边界了：

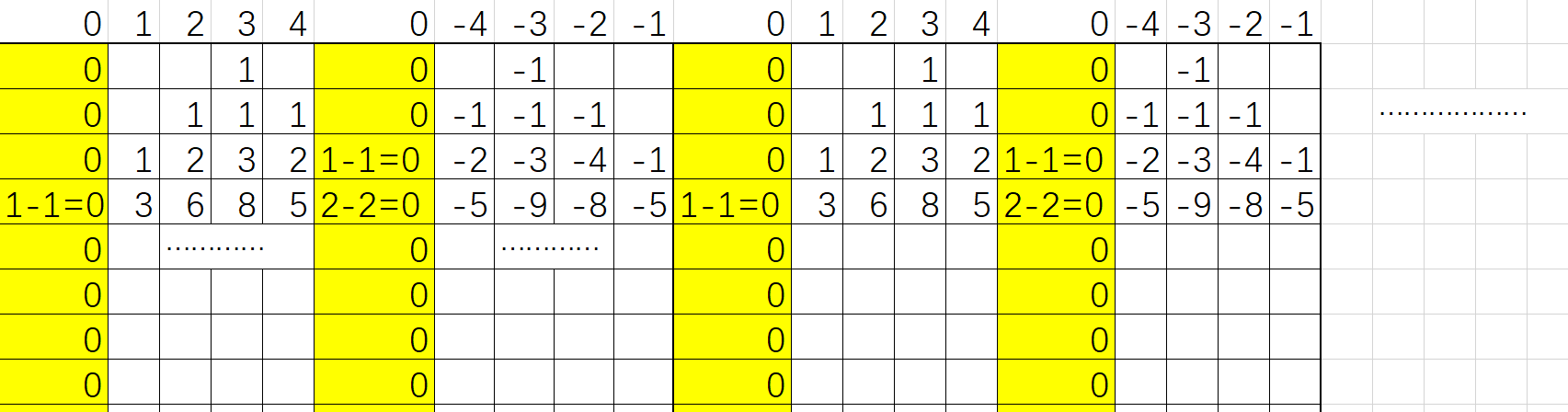
这样的话可以看成做循环卷积 .

王的象棋世界

有一个王在 \(n\times m\) 的棋盘上，\(q\) 次询问王走 \(n-1\) 步从 \((1,s)\) 走到 \((n,t)\) 的方案数 .

数据范围：\(2\le s,t\le m\le 10^5\)，\(m\le n\le 10^9\) .

根据前述结论就是要计算：

\[[x^t](x^s+x^{-s})(x+1+x^{-1})^{n-1}\pmod{x^{2m+2}-1} \]

做一下快速幂就可以随意 \(\Theta(\mathsf M(m)\log n+q)\) 了 .

其实这个理解很有生活了，毕竟一般反射容斥斜率也都是很规整的，都能套用这个做法的逻辑来简单理解 .

图