Jijidawang

小题狂练 (E)

目录

目录

[省选联考 2020 B 卷] 丁香之路

对于固定起点、终点 \(s,t\)，相当于给一个边集 \(E_0\)，找一个尽可能小的边集 \(E\supseteq E_0\) 使得 \(E\) 对应的子图中存在一条 \(s-t\) 的欧拉路 .

考虑先加一条 \((s,t)\) 转为欧拉回路，然后首先把 \(E\) 的每个点度数补成偶数且连通尽量多的点：考虑每个 \(2\nmid\deg(u)\) 的 \(u\)，然后按顺序两两匹配，对于一组 \((u,v)\)，依次连 \((u,u+1),\cdots,(v-1,v)\) 来使得它们的度数奇偶性翻转 .

操作完之后只需要再连一些边使得每个度数不为 0 的点都连通，这个可以使用最小生成树简单解决 .

时间复杂度 \(\tilde\Theta(n^2+m)\) .

[JSOI2019] 精准预测

类似 2-SAT 地，对每个时刻 \(t\) 上的居民 \(x\) 建立结点 \(\operatorname{alive}(t,x),\operatorname{dead}(t,x)\)，然后刻画出 0 操作和 1 操作还有不能复活的限制之后就是问对于每个 \(\operatorname{alive}(T+1,x)\) 有多少个 \(y\) 使得 \(\operatorname{alive}(T+1,x),\operatorname{alive}(T+1,y)\) 都不能到 \(\operatorname{dead}(T+1,y)\) . 显然只有 \(O(n+m)\) 个点是关键的，那么大力建图后直接 bitset 跑 DAG 可达性就可以了 .

由于这个题比较毒瘤所以需要一系列卡常：

  • 时间上：需要使用 DFS 进行 DP，不要写 BFS 的拓扑排序；注意到只有限制中作为 \(x\) 的位置才可能有用，\(y\) 的位置并没有什么用，于是可以把每个 \(y\) 的限制对应的时间改成离它最近的作为 \(x\) 操作数的时间，这个操作大概可以让点数除以二 .
  • 空间上：由于开不下全的 bitset 所以需要分段做，令块长为 \(B\) 则每次只记录 \(B\) 个点的可达性，做 \(\frac nB\) 次 .

[AGC026D] Histogram Coloring

先考虑如果矩形是整的那么就考虑每行相当于必须填下一行的 flip，如果下一行全同色则也可以和下一行填一样的 .

那么对于任意棋盘也可以考虑每次填最下面一行，但是此处删掉一行之后序列可能会分裂成若干部分，此处可以递归进入子问题 . 大概是一个笛卡尔树的结构 .

[AGC049D] Convex Sequence

如果 \(a\) 单调增的话就是要求 \(a\) 的差分数组单调增并且它的二阶前缀和等于 \(m\)，那么 Abel 变换拆一下贡献可以得到方案数为 \(\displaystyle p(m)=[x^m]\prod_{k\ge1}\dfrac{1}{1-x^{k(k+1)/2}}\) .

对于原题来说考虑枚举最小值就变成了两个单调增的问题卷起来，相当于要算 \(O(n)\) 个：

\[[x^m]\prod_{k=1}^a\dfrac{1}{1-x^{k(k+1)/2}}\prod_{k=1}^b\dfrac{1}{1-x^{k(k+1)/2}} \]

然而发现本质不同的 \((a,b)\) 对只有 \(O(\sqrt m)\) 种，于是直接动态维护每个位置的系数，只需要每次乘或除一个 \(\frac1{1-x^c}\) .

总时间复杂度 \(O(m\sqrt m)\) 可以通过 . 我们 GF 批是这样的

[AGC058D] Yet Another ABC String

符号化容斥初探， specify 部分贺的讲题课件的，似乎和目前能看见的题解的处理方法都不太一样 .

[CEOI2014] The Wall

首先注意到城墙一定包含到每个村庄的左上角的最短路，可以调整证明：

那么求出最短路树之后就是要求包含所有最短路的最小城墙，把每个点拆成四个方向的接头之后做最短路就可以了：

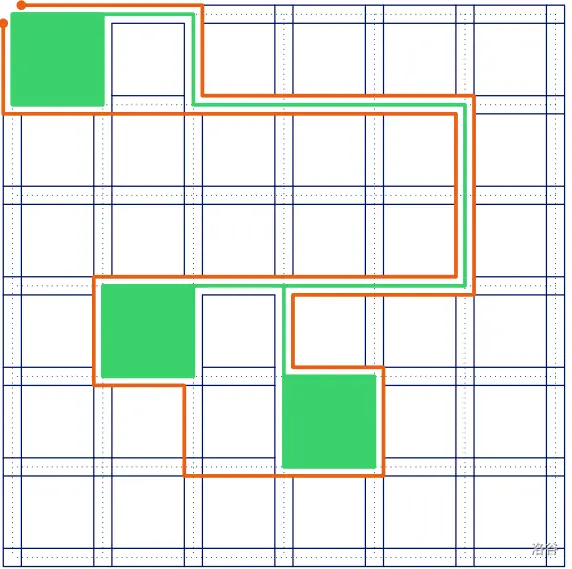
时间复杂度 \(\Theta(\operatorname{SSSP}(nm,nm))\)，可以通过 .

[ABC217H] Snuketoon

Slope Trick 模板 . 后称连续的凸分段线性函数为折线函数 .

首先朴素 DP，\(dp_{i,j}\) 表示时刻 \(t_i\) 位于 \(j\) 的最小代价，则：

\[dp_{i,j}=\min_{|k-j|\le t_i-t_{i-1}}\{dp_{i-1,k}\}+f_{d_i}(x_i,j) \]

由于 \(f\) 是折线函数，转移相当于平移取 min，所以 \(dp\) 也是折线函数 . 然后开两个堆分别维护左右凸壳就行了 .

[POI2010] MOS-Bridges

二分答案后变成求混合图欧拉回路，也就相当于给每条无向边定向后图是欧拉图 .

有向图是欧拉图当且仅当入度和出度相等，首先特判存在 \(u\) 使得 \(2\nmid\deg(u)\) 时无解 .

对于其余情况，先随便定向，然后算出每个点 \(u\) 的入度 \(\operatorname{in}(u)\) 和出度 \(\operatorname{out}(u)\) .

令源点为 \(s\)、汇点为 \(t\)，那么考虑这样建立最大流模型：

  • 对于 \(\operatorname{in}(u)>\operatorname{out}(u)\) 的点 \(u\)，连一条 \(s\to u\) 容量为 \(\frac{\operatorname{in}(u)-\operatorname{out}(u)}2\) 的边，表示需要流入这么多流量平衡度数 .
  • 对于 \(\operatorname{in}(u)<\operatorname{out}(u)\) 的点 \(u\)，连一条 \(u\to t\) 容量为 \(\frac{\operatorname{out}(u)-\operatorname{in}(u)}2\) 的边，表示需要流出这么多流量平衡度数 .
  • 对于原先的一条定向为 \(u\to v\) 的双向边 \(u,v\)，连一条 \(v\to u\) 容量为 \(1\) 的边，表示可以流 \(1\) 翻转这条边的方向 .

然后计算 \(s\to t\) 的最大流即可 . 如果满流说明存在欧拉回路，接下来只需要看每条 \(v\to u\) 的边是否流即可得到每条边的方向，接下来跑有向图欧拉回路即可得到方案 . 时间复杂度 \(O(\operatorname{maxflow}(n,n+m)\log V)\)，可以通过 .

[SDOI2016] 墙上的句子

大概一个二选一模型的套路吧 .

首先把回文的丢掉，然后相当于 \(n+m\) 组字符串上的问题 . 如果 \(x>x^{\sf R}\) 那么令 \(x\gets x^{\sf R}\) 这样每个位置的字典序都小于翻转后的字典序 .

建立最小割模型：源汇点为 \(s,t\)，首先对于每个串都连 \(x\to x^{\sf R}\)，容量为 \(2\) .

对于阅读顺序确定的串，若正串一定出现则连 \(s\to x\)，若反串一定出现则连 \(x^{\sf R}\to t\)，容量均为 \(+\infty\) .

关于阅读顺序不确定的串，考虑到所有串的阅读方向肯定都是一样的，对于每个字符串簇 \(u\) 和其上的字符串 \(x\) 连容量为 \(+\infty\) 的边 \(u\to x\) 和 \(x^{\sf R}\to u\) 来绑定每个字符串即可 .

[ARC175F] Append Same Characters

由于某些原因我先不写证明，直接给出以下结论：

  • \(\operatorname{comp}(X,YX)=\operatorname{comp}(X,Y^{\infty})\) .
  • \(\operatorname{comp}(XY,YX)=\operatorname{comp}(X^{\infty},Y^{\infty})\) .
  • 对于 \(XY\neq YX\)，\(\operatorname{LCP}(XY,YX)=\operatorname{LCP}(X^{\infty},Y^{\infty})\) .

首先相当于给每个字符串后面加一个字符串 \(X\) 并最小化逆序对个数加 \(|X|\) .

考虑什么时候在字符串 \(A<B\) 后面加字符串 \(X\) 会翻转其大小关系 \(AX>BX\)，首先显然有 \(A\) 是 \(B\) 的前缀，那么计算 \(B\) 去掉 \(A\) 之后得到的字符串 \(Y\) 后就相当于 \(X>YX\)，根据结论可以知道相当于 \(X>Y^{\infty}\) .

那么在 Trie 树上找到所有的 \(Y\)，这是 \(O(\sum|s_i|)\) 级别的，然后利用结论 \(\operatorname{comp}(XY,YX)=\operatorname{comp}(X^{\infty},Y^{\infty})\) 给所有 \(Y^{\infty}\) 排序，这样只需要枚举一段前缀被影响，然后计算逆序对和最小的合法 \(|X|\) 即可 .

首先对于逆序对可以直接在 Trie 树上计算有多少对逆序对涉及到某个 \(Y\)，这是简单的 . 对于最小的合法 \(|X|\) 就相当于要计算两个相邻的 \(Y^{\infty}\) 的 LCP，直接用结论就可以了（\(X\) 比所有 \(Y^{\infty}\) 大的情况要单独算一下）.

时间复杂度 \(O(n+\sum|s_i|\log^2n)\)，瓶颈在对 \(Y^{\infty}\) 排序上 . 如果使用 SA 比较就可以去掉一个 log，虽然跑得也没 Hash 快吧 .

[Ynoi2008] stcm

在 DFS 序上用猫树分治，每次处理跨过中点的询问，由于子树在 DFS 树上对应的区间一定不交所以可以双指针完成 .

大约 \(3n\log_2n\) 次 1 操作轻松通过 . 注意最后还得输出一个 !（

[AGC064C] Erase and Divide Game

如果给的不是区间而是数的话只需要从低往高建 Trie 树然后 DP 就可以了 .

如果改成区间的话首先把区间拆成 \(O(\log V)\) 个整的区间，对于每个区间 \([l,l+2^k)\) 相当于在 Trie 树上前 \(k\) 步随便走、后 \(k\) 步按指定方法走 . 那么可以考虑让这样的连续段一起进行转移，在 Trie 树上从深向浅考虑动态维护当前的区间，每次让区间里所有结点同时往上走一步进行转移即可 .

时间复杂度 \(O(n\log V)\) .

[NOI2016] 优秀的拆分

首先只需要求以每个位置开头或结尾的平方串 \(AA\) 个数即可 .

考虑枚举 \(A\) 的长度 \(L\)，将字符串中 \(L\) 的倍数位置标记，那么一个平方串一定跨越两个相邻标记点 .

枚举相邻标记点 \(p,q\)，计算 \(P=\operatorname{LCP}(\operatorname{suf}(p),\operatorname{suf}(q)),\,Q=\operatorname{LCS}(\operatorname{pre}(p),\operatorname{pre}(q))\)，那么如果 \(P,Q\) 不重合则无解，否则平方串 \(AA\) 中第一个 \(A\) 的结尾只能取 \(P,Q\) 重合的位置，可以画图感受一下 .

那么就 \(\Theta(n\log n)\) 了（这里使用 SA 求 LCP 和 LCS）.

[NOI2023] 字符串

首先条件显然等价于 \(s[i:i+2l-1]<s[i:i+2l-1]^{\sf R}\) .

首先弱化到 \(\operatorname{suf}(i)<\operatorname{pre}(i+2l-1)^{\sf R}\)，可以通过把字符串翻转过来复制到后面来转为后缀比较，于是使用 SA 即可转为二维数点 .

然而可以发现在 \(\operatorname{suf}(i)<\operatorname{pre}(i+2l-1)^{\sf R}\) 且 \(s[i:i+2l-1]\) 回文的时候会多算，考虑减掉这部分贡献 。 虽然看似有点儿三维偏序的风味，但是 Manacher 求最长回文半径后显然大小只会在回文半径外面的一位比较完毕，所以其实也是二维数点 .

总之可以单次 \(O((n+q)\log n)\) 解决，在洛谷上可能需要稍微卡一下常数 .

CF1276F Asterisk Substrings

把子串分为 \(S,\texttt{*}S,S\texttt{*},S\texttt{*}T\) 几类分别统计 . 前三类平凡，只需要关心最后一类 .

在 SAM 上考虑对于 endpos 相同的 \(S\) 它们对应的 \(T\) 的开头位置也是相同的，那么就是要求一些后缀的并的本质不同前缀个数 . 根据 SA 的理论这个就等于排序后的长度和减去相邻的 LCP 长度和，可以随便拿什么数据结构维护 .

时间复杂度 \(O(n\log n)\)，稍微多点 log 也能过 .

QOJ #8079. Range Periodicity Query

注意到对于长度大于 \(p\) 的字符串 \(S_k\)，若 \(p\) 不是 \(S_k\) 的 period，那么它必然也不是 \(S_{k+1}\) 的 period .

那么可以二分出一个 period \(p\) 所存活的时间区间，扫描线维护单点修改区间 min 即可 .

CF1799F Halve or Subtract

严格 wqs 二分 .

[AGC032E] Modulo Pairing

调整法易证排序后答案一定是一个前缀从开头结尾向中间两两匹配且和都 \(<m\)、一个后缀从开头结尾向中间两两匹配且和都 \(\ge m\) .

先不管和 \(\ge m\) 的限制，那么显然分界点越往左越优 . 于是二分分界点判断一下匹配后和是否 \(\ge m\) 即可 .

时间复杂度 \(\Theta(n\log n)\) .

[AGC014D] Black and White Tree

首先立刻注意到如果某个点有两个叶子作为儿子那么先手选这个点后手不可能同时堵住每个儿子从而先手就赢了 .

那么可以想到过程大概就是先手取一个点、后手取掉它对应的叶子，然后转化为少两个点的子问题 . 通过观察可以发现相当于问树是否存在完美匹配，可以随便做 .

[AGC016F] Games on DAG

相当于问有多少个子图满足 \(\operatorname{SG}(1)\neq\operatorname{SG}(2)\)，首先容斥改成算 \(\operatorname{SG}(1)=\operatorname{SG}(2)\) 的情况.

从小到大考虑每种 SG 函数：考虑把一个每个点 SG 都不小于 \(k\) 的集合 \(S\) 分为 SG 等于 \(k\) 的集合 \(T\) 和 SG 大于 \(k\) 的集合 \(S\setminus T\) 两部分（天然要求 \(1,2\) 要么同时在 \(T\) 中要么同时在 \(S\setminus T\) 中），那么只要求：

  • \(T\) 内部不能有连边 .
  • 每个 \(u\in S\setminus T\) 都必须至少连一条到 \(T\) 的边 .

于是可以直接 DP，预处理一点东西就可以简单做到 \(\Theta(3^nn)\) 了（据说可以到 \(\Theta(3^n)\)）.

CF335F Buy One, Get One Free

首先一个基本的想法是每次取两个最大值 \(c\)，然后对于以前的匹配 \(a-b\)，可以考虑拆散成 \(a-c,\,b-c\)，两种情况取 max，过程中用堆动态维护一下决策点 .

然而发现这个策略有点虚假，还需要支持反悔：\(a-c,\,b-c\to a-b,\,c,c\) . 那么就把 \(2c-a-b\) 也当成物品放进堆里就可以了 . 由于反悔之后相当于 \(b-c\) 又独立出来了（可以继续参与结合），所以匹配的时候不能把 \(b\) 从堆里弹出来，由于 \(2c-a-b>b\) 时才会做 \(a-b,\,c,\,c\to a-c,\,b-c\) 所以肯定先反悔再匹配 \(b\)，不会有问题 .

时间复杂度 \(O(n\log n)\) .

洛谷 P5592 美德的讲坛

大豆之力，充满全身！大致复读一下以前写过的题解，其实分治结构还是比较自然的 .

首先 \(x\gets x-1\) 并特判 \(x=0\) . 先做单组询问，假设当前在 \(b\) 位下考虑问题，即 \(a_i\in[0,2^b)\) .

如果 \(x<2^{b-1}\)，那么一个合法子集的 \(b\) 位及以上必须相同，按 \(b\) 位及以上划分集合即转为 \(x\le2^{b-1}\) 的情况 .

对于 \(x\ge2^{b-1}\)，考虑对于每个 \(a_i\oplus a_j\le x\) 连边 \(i-j\)，不难发现因为 \(b\) 位及以上的位相同的数一定会两两连边所以按 \(b\) 位分组则问题可以刻画为两个团 \(A,B\) 间连若干边求最大团 .

考虑分治，将 \(A,B\) 按 \(b-1\) 位划分为四个团 \(A_0,A_1,B_0,B_1\)：

  • 如果 \(x\) 的第 \(b-1\) 位为 1，则只要考虑第 \(b-1\) 位顶格的情况，别的情况可以随便放，那么就是：

    \[f(A,B)=f(A_0,B_1)+f(A_1,B_0) \]

  • 如果 \(x\) 的第 \(b-1\) 位为 1，则类似地，有：

    \[f(A,B)=\max\{|A|,|B|,f(A_0,B_0),f(A_1,B_1)\} \]

实际实现时可以在 0-1 Trie 上做 . 对于多组询问由于一次修改只会改 \(O(\log V)\) 个点，记忆化就可以了，注意这里要用数组不要用 map 或者 umap，会被卡常 . 时间复杂度 \(O((n+q)\log V)\) .

[AGC010C] Cleaning

特判 \(n=2\)，然后选择一个度数大于 \(2\) 的点当根，那么无根树上的叶子就转为有根树上的叶子了 .

令 \(f_u\) 表示 \(u\) 向上延伸的路径数量，\(s_u=\sum_{v\in\operatorname{son}(u)}f_v\) . 讨论 \(u\) 点路径的去向容易得到：

\[a_u=\dfrac{s_u-f_u}2+f_u\iff f_u=2a_u-s_u \]

那么其实可以直接 DFS 一遍把所有 \(f\) 都求出来，然后只需要分别判断 \(0\le f_u\le a_u\)、\(\max_{v\in\operatorname{son}(u)}f_v\le a_u\) 且 \(f_{root}=0\) 即可 . ←关于第二个条件，考虑链之间互相抵消的结构类似一个序列每次取两个数减一问能否归零这种问题，于是调用这个问题的结论可以发现这里要求 \(\max f_v\le \dfrac{s_u-f_u}2=a_u\)，否则无法通过操作归零 .

时间复杂度 \(\Theta(n)\) .

UOJ #52. 元旦激光炮

元旦激光炮！

首先把下标改成从 \(1\) 开始方便叙述 . 取 \(p=\lfloor\frac k3\rfloor\)，找到 \(a_p,b_p,c_p\) 中的最小值，容易发现其排名最多为 \(3p-2<k\)，所以可以把对应数组中比这个位置小的位置删去，即转为 \(len\gets len-p,\,k\gets k-p\) 的子问题 .

容易发现询问次数约为 \(\log_{2/3}k\)，足以通过本题 .

[AGC010D] Decrementing

首先样例提示我们，如果有 \(1\) 的话就只是一个判断奇偶性的问题 .

对于一般的情况，如果开局有奇数个偶数，先手每次选一个偶数减一，后手怎么做也无法改变偶数个数的奇偶性 . 如果开局有偶数个偶数，先手只能期望能全局除以二来翻盘，此时必须只有恰好一个奇数，否则就会被后手控制住 . 那么对于前面这种翻盘的情况，相当于先后手翻转然后转化为子问题 .

模拟上述过程即可 \(O(n\log^2A)\) 解决（有人说其实是单 log，但是我没感受出来）.

[AGC070A] Multiples in the String

突然又看到这个题了，于是写一下题解，魔怔一下（

如果一个分数 \(\frac 1p\) 对于每个 \(1<k<p\)，\(\frac kp\) 的循环节都是 \(\frac 1p\) 的循环节的循环位移，那么 \(\frac 1p\) 是走马灯数 . 容易验证，若 \(\frac 1p\) 在 \(b\) 进制下是走马灯数，那么 \(b\) 是 \(p\) 的原根（可以写一下同余方程）.

对于一个走马灯数 \(p\)，可以这样构造：\(X=p,\,S=\overline p\overline p\)（拼接）. 关于找 \(p\) 的话只需要从 \(1000\) 往上枚举 \(p\) 然后检验 \(10\) 是否是原根就可以找到一个走马灯数 \(p\) 了！这里最小的解是 \(p=1019\) .

[AGC010E] Rearranging

其实好像严谨证明还挺难的，所以感性理解一下跑路了 .

首先可以感受一下最终状态大概是若干段下降的段，然后一个上升的位置需要满足这个位置和前面段里的每个数都不互质 . 那么对于每个 \(a_u\not\perp a_v\) 连 \(u-v\) 之后就相当于要把每个连通块定向成一个 DAG 使得最大拓扑序最小 . 这里可以 DFS 每次贪心地每次选一个编号最小的出边进入来完成定向，这样编号比较大的点在 DFS 树上会比较深，于是拓扑序会尽可能小 . 注：实现上可以只连生成树上的边，忽略其它边（因为显然不会对拓扑序有贡献）.

时间复杂度 \(\Theta(n^2\log V)\) .

CF804E The same permutation

首先交换一次逆序对奇偶性翻转，所以 \(\binom n2\) 至少得是偶数才能有解，也就是 \(n\bmod 4>1\) 无解 .

那么可以猜一下其它的都有解，也就只需要构造 \(n\bmod 4=0,1\) 的情况 . 先考虑 \(n\bmod 4=0\) 的情况，可以自然地考虑四个元素分一段，构造可以直接搜出来，挂一下课件：

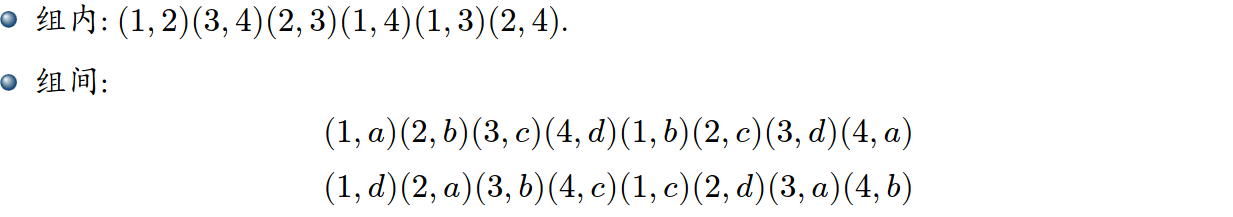
对于 \(n\bmod 4=1\) 的情况，注意到把交换操作 \((i,j)\) 改成 \((i,n),(i,j),(j,n)\) 效果不变，那么在 \(n-1\) 的构造里找到一些 \((2i,2i+1)\) 的交换用上面的操作改掉就可以了 .

洛谷 P7512 「Byakkai OI 2021」Eaquira

alpha 题 /se

由于组合结构比较魔怔，所以这里快进到生成函数，刻画可以看官方题解：

\[[x^n]\dfrac{2+F(x)}{1-G(F(x),w)}\text{ where }F(x)=\dfrac x{(1-x)^3},\,G(x,w)=\dfrac{xw(1+w)}{(1-xw)^2} \]

有理分式远端求值，Bostan-Mori 即可！时间复杂度 \(\Theta(\mathsf M(n))\) .

[SNOI2020] 取石子

调用 Fibonacci Nim 的结论（需要稍微调整一下）即可得到答案的表达式：

\[\mathrm{ans}=\sum_{i=1}^{n-1}[\operatorname{lowbit}(i)\le k] \]

其中 \(\operatorname{lowbit}(x)\) 是 \(x\) 在 Zeckendorf 表示下的最低位的值 . 那么数位 DP 就可以了 .

CodeFestival2017qualB Largest Smallest Cyclic Shift

首先假定 \(\gcd(X,Y,Z)=1\)，否则可以转为 \(\gcd(X,Y,Z)\) 个这样的问题 .

考虑这样一个问题：给定 Lyndon 串组成的集合 \(S\)，要求拼成一个字典序最大的字符串 .

考虑每次取字典序最小的字符串和字典序最大的字符串拼起来，由于对于 Lyndon 串 \(u<v\)，\(uv\) 也是 Lyndon 串，所以问题随时形式不变 . 正确性邻项交换可证（需要注意到对于 Lyndon 串 \(u,v\)，\(\operatorname{comp}(u,v)=\operatorname{comp}(uv,vu)\)）.

[AGC006E] Rotate 3x3

首先可以简单将问题转写为对于一个序列 \(p\)，满足每个位置的绝对值构成一个排列，每次可以选三个相邻的数翻转并取相反数，问能否还原为单位排列 .

断言：若 \(p\) 合法，则将 \(p_i,p_{i+2}\) 同时取相反数后也合法 .

构造：

 1  2  3  4  5
-3 -2 -1  4  5
-3 -2 -5 -4  1
 5  2  3 -4  1
 5  2 -1  4 -3
 1 -2 -5  4 -3
 1 -2  3 -4  5   (中心构造方案 (2, 4))
-3  2 -1 -4  5
-3  4  1 -2  5
-1 -4  3 -2  5
-1  2 -3  4  5   (边界构造方案 (1, 3)，另一侧同理)

奇数/偶数位交换一次偶数/奇数位的符号翻转，对于奇偶性确定的情况根据上述断言可以随意调整 . 那么相当于只需要求奇数/偶数项位置逆序对的奇偶性就可以算出来绝对值归位后符号的奇偶性，然后判断奇偶性是否归位即可 .

CF715D Create a Maze

感觉不如三进制！如图所示（来源：CF Comment）：

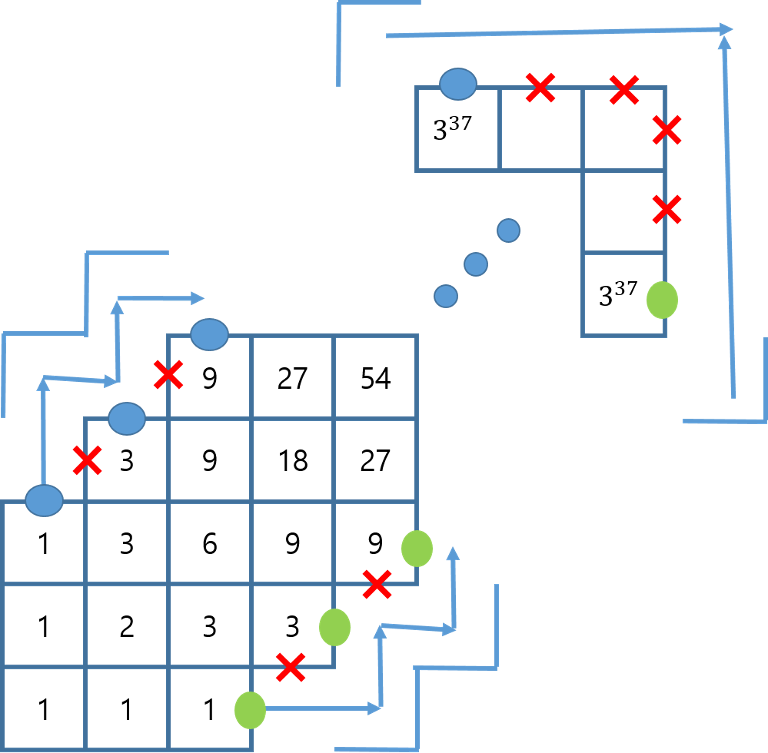
此处最坏 \(n=m=41,\,k=299\)，足已通过！

CF167C Wizards and Numbers

首先注意到若 \((a,b\bmod a)\) 后手必胜，那么 \((a,b)\) 先手必胜 . 否则由于减 \(a^k\) 不改变模 \(a\) 的值所以后面一定没有人会做取模操作 .

那么问题就转化为有 \(n\) 个石子，每次可以取 \(a,a^2,\cdots\) 个，不能取的输 . 断言：先手必胜当且仅当 \(n\bmod(a+1)\) 是偶数，可以使用类似 Bash 博弈的模仿证明 .

时间复杂度 \(O(T\log(a+b))\) .

posted @ 2024-12-22 21:21  yspm  阅读(231)  评论(9)    收藏  举报
😅​